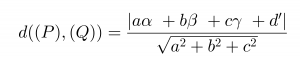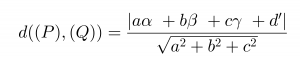Công thức Khoảng cách giữa 2 mặt phẳng

Khi biết phương trình của hai mặt phẳng ta dễ dàng tính được khoảng cách giữa 2 mặt phẳng này. Bài viết này gửi tới người chơi công thức tổng quát và những tỉ dụ có lời giải cụ thể, và dưới đây tintuctuyensinh sẽ tổng hợp Công thức Khoảng cách giữa 2 mặt phẳng nhe

1. Công thức tính khoảng cách giữa 2 mặt phẳng song song

Trong không gian Oxyz, cho nhị mặt phẳng song song với nhau với phương trình lần lượt là (α): ax + by + cz + d1 = 0 và (β): ax + by + cz + d2 = 0. Khoảng cách giữa nhì mặt phẳng này được xác định theo công thức

d((α); (β)) = |d1–d2|a2+b2+c2√ với d1 ≠ d2.

Chú ý: Nếu d1 = d2. =≫ nhì mặt phẳng trùng nhau => d((α); (β)) = 0

2. Bài tập có lời giải cụ thể

Bài tập 1. Trong không gian Oxyz, có hai mặt phẳng có phương trình lần lượt là (α): x – 2y + z + 1 = 0 và (β): x – 2y + z + 3 = 0. Hãy tính khoảng cách giữa 2 mặt phẳng?

hướng dẫn giải

Ta thấy nhì mặt phẳng này đồng thời với nhau nên khoảng cách giữa 2 mặt phẳng được xác định theo công thức

d((α); (β)) = |1–3|12+(–2)2√+12=6√3

Kết luận: d((α); (β)) = 6√3

Bài tập 2. nhì mặt phẳng (α) // (β), cách nhau 3. Biết phương trình của mỗi mặt phẳng là (α): 2x – 5y – 3z + 1 = 0 và (β): ax + by + cz + d2 = 0. Hãy xác định các hệ số của phương trình mặt phẳng (β).

hướng dẫn giải

do (α) // (β) => a = 2; b = – 5 và c = – 3

Mặt khác: d((α); (β)) = 3 => |1–d1|22+(–5)2+(–3)2√=3⇔d1=338−−√–1

Kết luận: Phương trình mặt phẳng (β): 2x – 5y – 3z + (338−−√–1) = 0

2. Công thức tính khoảng cách giữa 2 mặt phẳng trong không gian

Công thức tính khoảng cách giữa 2 mặt phẳng trong không gian là thắc bận bịu được rất nhiều người niềm nở. Đây là một câu hỏi vô cùng cần thiết để giúp Cả nhà có thêm tri thức song song thuận lợi trả lời bài tập của mình. Ngay hiện nay mình hãy cùng nhau theo dõi và giải một số bài toán nhé!

định nghĩa khoảng cách giữa 2 mặt phẳng trong không gian

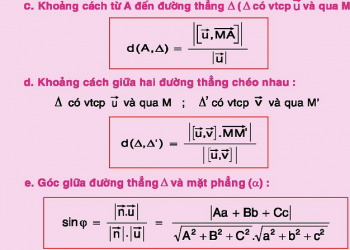
trước nhất, ta nhắc lại định nghĩa khoảng cách từ một điểm M lên mặt phẳng (P) là khoảng cách giữa M và hình chiếu của nó trên mặt phẳng (P). Ký hiệu là d(M,(P)).

Cho hai mặt phẳng (P) và (Q) đồng thời với nhau. Khoảng cách giữa mặt phẳng (P) và (Q) là khoảng cách từ một điểm M bất cứ trên mặt phẳng (P) tới mặt phẳng (Q) hoặc trái lại. Ký hiệu là d((P),(Q))

Công thức tính khoảng cách giữa 2 mặt phẳng trong không gian

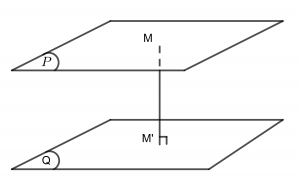
Ngay bây giờ hãy cùng chúng tôi đi mày mò công thức tính khoảng cách giữa 2 mặt phẳng trong không gian. Qua đó Anh chị sẽ dễ ợt giải được những bài tập tương tác tới tính khoảng cách giữa 2 mặt phẳng trong không gian

Cho nhì mặt phẳng (P), (Q) song song trong không gian. Phương trình của chúng đều có thể đưa về dạng:

(P): ax+by+cz+d=0 và (Q): ax+by+cz+d’=0 (a²+b²+c²>0 và d≠d’)

Khi đó giả sử M(α;β;γ) thuộc mặt phẳng (P) ta có: aα+bβ+cγ=-d. Khoảng cách giữa (P) và (Q)chính là khoảng cách giữa M và (Q). bởi đó: