Contents
Diện tích của một công thức tam giác đều
Công thức về diện tích của một tam giác đều được cho là:
| Diện tích tam giác đều (A) = (√3 / 4) a 2 |
Trong đó a = chiều dài các cạnh
Tìm hiểu thêm về tam giác cân, tam giác đều và tam giác vô hướng tại đây.
Tính xác định diện tích tam giác đều
Có ba phương pháp để suy ra công thức về diện tích của tam giác đều. Họ đang:
- Sử dụng công thức tam giác cơ bản
- Sử dụng cấu trúc hình chữ nhật
- Sử dụng lượng giác
Tính diện tích tam giác đều bằng công thức tam giác cơ bản
Lấy một tam giác đều cạnh “a” đơn vị. Sau đó, vẽ một đường phân giác vuông góc với đáy của chiều cao “h”.
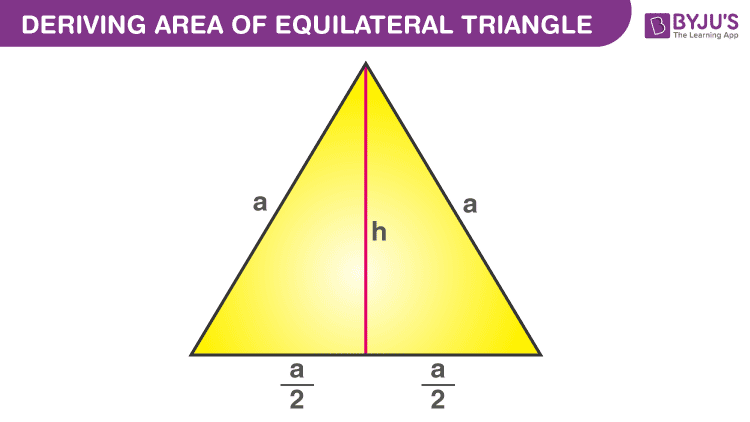

Diện tích hình thành của tam giác đều
Hiện nay,
Diện tích tam giác = ½ × cơ sở × chiều cao
Ở đây, base = a và height = h
Bây giờ, áp dụng Định lý Pythagoras trong tam giác.
a 2 = h 2 + (a / 2) 2
⇒ h 2 = a 2 – (a 2/4 )
⇒ h 2 = (3a 2 ) / 4
Hoặc, h = ½ (√3a)
Bây giờ, hãy đặt giá trị của “h” vào diện tích của phương trình tam giác.
Diện tích tam giác = ½ × cơ sở × chiều cao
⇒ A = ½ × a × ½ (√3a)
Hoặc, Diện tích tam giác đều = ¼ (√3a 2 )
Tính diện tích của tam giác đều bằng cách sử dụng cấu trúc hình chữ nhật
Xét một tam giác đều có các cạnh bằng “a”.

Tam giác đều
- Bây giờ, vẽ một đường thẳng từ đỉnh trên cùng của tam giác đến trung điểm của đáy tam giác, như vậy, chia đáy thành hai nửa bằng nhau.
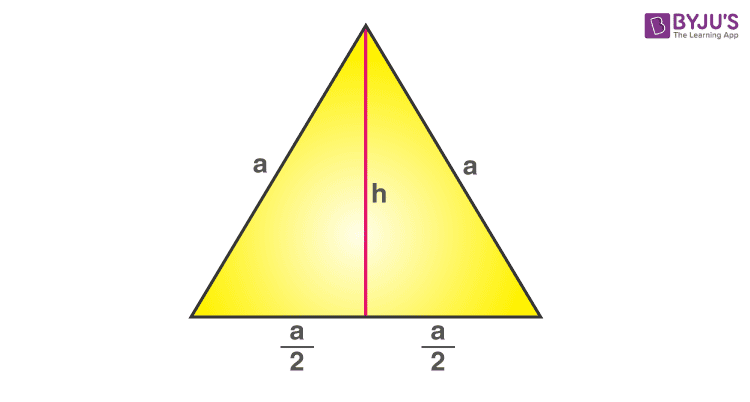

Diện tích tam giác đều
- Bây giờ cắt dọc theo đường thẳng và di chuyển nửa còn lại của hình tam giác để tạo thành hình chữ nhật.


Làm thế nào để tìm diện tích tam giác đều?
Ở đây, chiều dài của tam giác đều được coi là ‘a’ và chiều cao là ‘h’
Vậy diện tích tam giác đều = Diện tích hình chữ nhật = ½ × a × h …………. (Tôi)
Một nửa của hình chữ nhật là một tam giác vuông như hình trên.
Qua đó, áp dụng Định lý Pythagoras:
⇒ a 2 = h 2 + (a / 2) 2
⇒ h 2 = (3/4) a 2
⇒ h = (√3 / 2) a …………… (ii)
Thay giá trị của (ii) vào (i), ta có:
Diện tích tam giác đều
= (½) × a × (√3 / 2) a
= (√3 / 4) a 2
Tính diện tích tam giác đều bằng lượng giác
Nếu cho trước hai cạnh của một tam giác, thì chiều cao có thể được tính bằng cách sử dụng các hàm lượng giác. Bây giờ, chiều cao của tam giác ABC sẽ là-
h = b. Sin C = c. Sin A = a. Tội lỗi B
Bây giờ, diện tích ABC = ½ × a × (b. Sin C) = ½ × b × (c. Sin A) = ½ × c (a. Sin B)
Bây giờ, vì nó là một tam giác đều nên A = B = C = 60 °
Và a = b = c
Diện tích = ½ × a × (a. Sin 60 °) = ½ × a 2 × Sin 60 ° = ½ × a 2 × √3 / 2
Vì vậy, Diện tích tam giác đều = (√3 / 4) a 2
Dưới đây là một thông tin ngắn gọn về tam giác đều:
Tam giác đều là gì?
Chủ yếu có ba loại tam giác là tam giác vô hướng, tam giác đều và tam giác cân. Một tam giác đều có tất cả ba cạnh bằng nhau và tất cả các góc bằng 60 °. Tất cả các góc trong một tam giác đều là đồng dư.
Tính chất của tam giác đều
Tam giác đều là tam giác có cả ba cạnh bằng nhau. Đó là một trường hợp đặc biệt của tam giác cân mà cạnh thứ ba cũng bằng nhau. Trong tam giác đều ABC, AB = BC = CA.
Một số tính chất quan trọng của tam giác đều là:
- Tam giác đều là tam giác có cả ba cạnh bằng nhau.
- Tam giác đều còn gọi là tam giác đều. Điều đó có nghĩa là, cả ba góc trong bằng nhau và giá trị duy nhất có thể là 60 ° mỗi góc.
- Nó là một đa giác đều có 3 cạnh.
- Một tam giác đều nếu và chỉ khi các đường tròn ngoại tiếp của bất kỳ ba trong số các tam giác nhỏ hơn có cùng khoảng cách với tâm.
- Một tam giác đều nếu và chỉ khi bất kỳ ba trong số các tam giác nhỏ hơn có cùng chu vi hoặc bằng nhau.
- Diện tích của một tam giác đều về cơ bản là lượng không gian chiếm bởi một tam giác đều.
- Trong một tam giác đều, đường trung tuyến, đường phân giác góc và đường vuông góc đều giống nhau và có thể được gọi đơn giản là đường phân giác vuông góc do các điều kiện đồng dạng.
- Trực tâm và trọng tâm của tam giác là cùng một điểm.
- Trong một tam giác đều, đường trung tuyến, đường phân giác và đường cao đối với tất cả các cạnh đều bằng nhau và là các đường đối xứng của tam giác đều.
- Diện tích của một tam giác đều là √3 một 2 /4
- Chu vi hình tam giác đều là 3a.
Câu hỏi ví dụ sử dụng công thức diện tích tam giác đều
Câu 1 : Tìm diện tích của một tam giác đều có chu vi là 12 cm.
Giải pháp :
Cho: Chu vi tam giác đều = 12 cm
Theo công thức: Chu vi của tam giác đều = 3a, trong đó “a” là cạnh của tam giác đều.
Bước 1: Tìm cạnh của một tam giác đều bằng chu vi.
3a = 12
a = 4
Như vậy, chiều dài của cạnh là 4 cm.
Bước 2: Tìm diện tích tam giác đều bằng công thức.
Diện tích, A = √3 a 2/4 đơn vị sq
= √3 (4) 2/4 cm 2
= 4√3 cm 2
Do đó, diện tích của tam giác đều đã cho là 4√3 cm 2
Câu 2 : Diện tích của một tam giác đều có cạnh 8 cm là bao nhiêu?
Giải pháp :
Diện tích của tam giác đều = √3 một 2 /4
= √3 × (8 2 ) / 4 cm 2
= √3 × 16 cm 2
= 16 √3 cm 2
Câu 3: Tìm diện tích của một tam giác đều có cạnh bằng 7 cm.
Giải pháp:
Được,
Cạnh bên của tam giác đều = a = 7 cm
Diện tích của một tam giác đều = √3 một 2 /4
= (√3 / 4) × 7 2 cm 2
= (√3 / 4) × 49 cm 2
= 21.21762 cm 2
Câu 4: Tìm diện tích của một tam giác đều có cạnh là 28 cm.
Giải pháp:
Được,
Cạnh bên của tam giác đều (a) = 28 cm
Chúng tôi biết,
Diện tích của một tam giác đều = √3 một 2 /4
= (√3 / 4) × 28 2 cm 2
= (√3 / 4) × 784 cm 2
= 339,48196 cm 2
Các câu hỏi thường gặp
Tam giác đều là gì?
Tam giác đều có thể được định nghĩa là một loại tam giác đặc biệt có tất cả các cạnh và góc trong bằng nhau. Trong một tam giác đều, số đo các góc trong là 60o.
Diện tích của một tam giác đều có nghĩa là gì?
Diện tích của tam giác đều được định nghĩa là khoảng không gian mà tam giác đều chiếm trong diện tích hai chiều.
Công thức diện tích tam giác đều là gì?
Để tính diện tích của một tam giác đều, công thức sau được sử dụng:
A = ¼ (√3a 2 )
Công thức tính chu vi của tam giác đều là gì?
Công thức tính chu vi hình tam giác đều là:
P = 3a