Định lý chân Hypotenuse – Giải thích & Ví dụ đơn giản nhất

Trong bài này, chúng ta sẽ tìm hiểu về định lý chân cạnh huyền (HL) . Giống như, SAS, SSS, ASA và AAS , nó cũng là một trong những định đề đồng dư của một tam giác.

Sự khác biệt là 4 định đề còn lại có thể áp dụng cho tất cả các tam giác trong khi Định lý Chân Hypotenuse chỉ đúng cho các tam giác vuông , bởi vì rõ ràng, cạnh huyền là một trong các chân của tam giác vuông.

Định lý chân Hypotenuse là gì?

Định lý chân cạnh huyền là một tiêu chuẩn được sử dụng để chứng minh liệu một tập hợp các tam giác vuông đã cho có đồng dư hay không.

Định lý chân cạnh huyền (HL) phát biểu rằng; một tập hợp các tam giác đã cho là đồng dư nếu độ dài tương ứng của cạnh huyền và một chân của chúng bằng nhau.

Không giống như các định đề đồng dư khác như; SSS, SAS, ASA và AAS, trong đó ba đại lượng được kiểm tra, với định lý chân cạnh huyền (HL), hai cạnh của tam giác vuông chỉ được xét.

Hình minh họa:

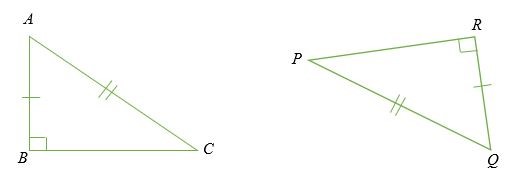
Chứng minh Định lý Chân Hypotenuse

Nếu sơ đồ trên, các tam giác ABC và PQR là các tam giác vuông với AB  =  RQ ,  AC = PQ.

Theo Định lý Pythagore,

AC ² = AB ² + BC ² và PQ ² = RQ ² + RP ²

Vì, AC = PQ, thay thế để có được;

AB ² + BC ² = RQ ² + RP ²

Nhưng, AB  =  RQ,

Bằng cách thay thế;

RQ ² + BC ² = RQ ² + RP ²

Thu thập các điều khoản like để có được;

BC ² = RP ²

Do đó, △ ABC ≅ △ PQR

ví dụ 1

Nếu PR ⊥ QS, chứng minh rằng PQR và PRS là đồng dư

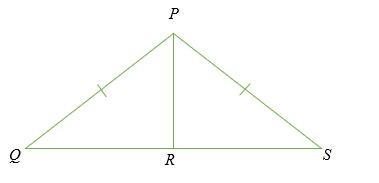
Giải pháp

Tam giác PQR và PRS là tam giác vuông vì cả hai đều có một góc 90 độ vào thời điểm R .

Được;

• PQ = PS(Hypotenuse)
• PR = PR(Mặt chung)
• Do đó, theo định lý Hypotenuse – Leg (HL), △PQR ≅ △ PR

Ví dụ 2

Nếu FB = DB, BA = BC , FB  ⊥ AE và DB ⊥ CE , chứng tỏ AE = CE.

Giải pháp

Theo quy tắc Hypotenuse Leg,

• BA = BC(cạnh huyền)
• FB = DB(cạnh bằng nhau)
• Vì ∆ AFB≅ ∆ BDC nên ∠ A = ∠ Do đó, AE = CE

Do đó đã chứng minh.

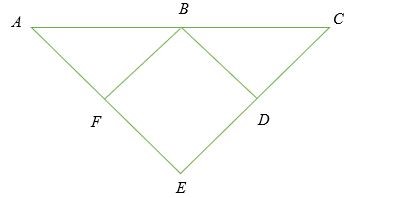
Ví dụ 3

Cho rằng ∆ ABC là tam giác cân và ∠ BAM = ∠ MAD . Chứng minh rằng M là trung điểm của BD.

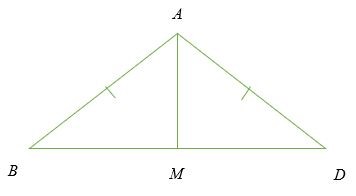
Giải pháp

Cho trước ∠ BAM = ∠ MAD thì đường thẳng AM là tia phân giác của ∠ BAD.

• AB = AD(cạnh huyền)
• AM = AM(chân chung)
• ∠AMB = ∠ AMD (góc vuông)
• Do đó, BM = MD.

Ví dụ 4

Kiểm tra xem ∆ XYZ và ∆ STR có đồng dư hay không.

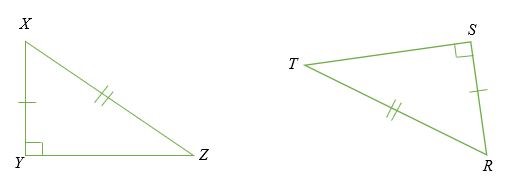
Giải pháp

• Cả ∆ XYZvà ∆ STR đều là tam giác vuông (có góc 90 độ)
• XZ = TR(cạnh huyền bằng nhau).
• XY = SR(Chân bằng)
• Do đó, theo định lý Hypotenuse -Leg (HL), ∆ XYZ≅∆ STR

Ví dụ 5

Cho : ∠ A = ∠ C = 90 độ , AB = BC . Chứng tỏ rằng △ ABD ≅ △ DBC.

Giải pháp

Được,

• AB = BC(chân bằng)
• ∠A = ∠ C (góc vuông)
• BD = DB(cạnh chung, cạnh huyền)
• Theo định lý Hypotenuse-Leg (HL), △ABD ≅ △ DBC

Xem thêm:

Các loại hình tam giác và tất tần tật thông tin về nó

Diện tích tam giác – Giải thích và ví dụ chi tiết dễ hiểu nhất

Ví dụ 6

Nếu ∠ W = ∠ Z = 90 độ và M là trung điểm của WZ và XY. Chứng tỏ rằng hai tam giác WMX và YMZ là đồng dạng.

Giải pháp

• △WMX và △ YMZ là các tam giác vuông vì cả hai đều có góc bằng 90 ⁰ (góc vuông)
• WM = MZ(chân)
• XM = MY(Hypotenuse)
• Do đó ,bởi cạnh huyền-Leg (HL) lý, △ WMX ≅ △ YMZ

Ví dụ 7

Tính giá trị của x trong các tam giác đồng dư sau.

Giải pháp

Cho hai tam giác đồng dạng, sau đó;

⇒2x + 2 = 5x – 19

⇒2x – 5x = -19 – 2

⇒ -3x = – 21

x = – 21 / -3

x = 7.

Do đó, giá trị của x = 7

Bằng chứng:

⇒ 2x + 2 = 2 (7) + 2

⇒14 + 2 = 16

⇒ 5x -19 = 5 (7) – 19

⇒ 35 – 19 = 16

Vâng, nó đã hoạt động!

Ví dụ 8

Nếu ∠ A = ∠ C = 90 độ và AB = BC. Tìm giá trị của x và y để hai tam giác ABD và DBC đồng dạng.

Giải pháp

Được,

△ ABD ≅ △ DBC

Tính giá trị của x

⇒ 6x – 7 = 4x + 2

⇒ 6x – 4x = 2 + 7

⇒ 2x = 9

⇒ x = 9/2

x = 4,5

Tính giá trị của y.

⇒ 4y + 25 = 7y – 5

⇒ 4y – 7y = – 5 – 25

⇒ -11y = -30

y = 30/11 = 2,73

Do đó, △ ABD ≅ △ DBC , khi x = 4,5 và y = 2,72.