Định lý cosin đơn giản rễ hiểu nhất 2021
23 Tháng Mười Hai, 2021Contents Định lý cosin Định luật côsin , định lý cơ bản của hình học phẳng Ơclit . Định luật Cosin là một định lý toán học mô tả mối quan hệ...
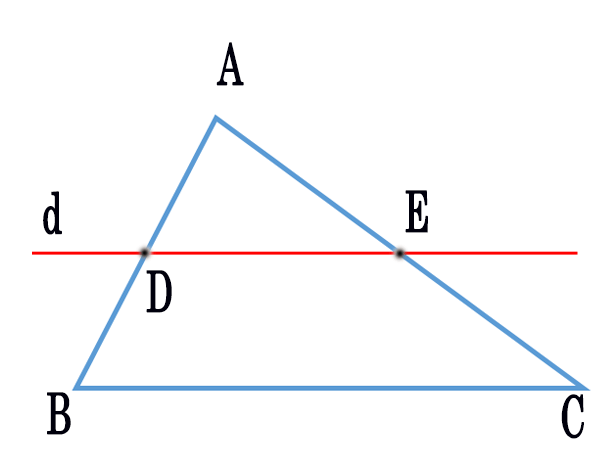
Định lý Thales (định lý talet) – Giải thích & Ví dụ
Bây giờ, sau khi chúng ta đã xem qua Định lý Góc nội tiếp, đã đến lúc nghiên cứu một định lý liên quan khác, đó là một trường hợp đặc biệt của Định lý Góc nội tiếp m, được gọi là Định lý Thales . Giống như Định lý Góc nội tiếp, định nghĩa của nó cũng dựa trên đường kính và các góc bên trong một đường tròn.

Contents
Định lý Thales phát biểu rằng:
Nếu ba điểm A, B và C nằm trên nửa đường tròn, theo đó đường thẳng AC là đường kính của đường tròn thì góc ∠ ABC là góc vuông (90 °).
Ngoài ra, định lý Thales có thể được phát biểu như sau:
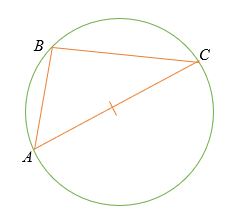

Bạn nhận thấy rằng định lý Thales là một trường hợp đặc biệt của định lý góc nội tiếp (góc ở tâm = hai lần góc nội tiếp).
Định lý Thales được quy cho Thales, một nhà toán học và triết học người Hy Lạp sống ở Miletus. Thales lần đầu tiên khởi xướng và xây dựng Nghiên cứu lý thuyết về Hình học để biến thiên văn học trở thành một khoa học chính xác hơn.
Có nhiều cách để chứng minh Định lý Thales . Cả kỹ thuật hình học và đại số đều có thể được sử dụng để chứng minh định lý này. Vì đây là chủ đề hình học nên chúng ta cùng xem một phương pháp cơ bản nhất dưới đây.
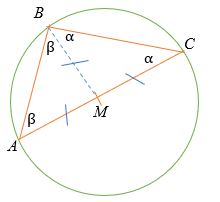

Theo định lý tổng tam giác,
∠ BAC + ∠ ACB + ∠ CBA = 180 °
β + β + α + α = 180 °
Nhân tố của phương trình.
2 β + 2 α = 180 °
2 (β + α) = 180 °
Chia cả hai bên cho 2.
β + α = 90 °.
Do đó, ∠ ABC = 90 °, do đó chứng tỏ
Hãy làm một vài bài toán ví dụ liên quan đến định lý Thales.
ví dụ 1
Cho điểm O là tâm của đường tròn dưới đây, hãy tìm giá trị của x.
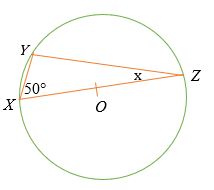

Giải pháp
Cho rằng đường thẳng XY là đường kính của đường tròn, thì theo định lý Thales,
∠ XYZ = 90 °.
Tổng các góc trong của một tam giác = 180 °
90 ° + 50 ° + x = 180 °
Đơn giản hóa.
140 ° + x = 180 °
Trừ 140 ° cho cả hai bên.
x = 180 ° – 140 °
x = 40 °.
Vì vậy, giá trị của x là 40 độ.
Ví dụ 2
Nếu điểm D là tâm của đường tròn dưới đây, hãy tính đường kính của đường tròn đó.
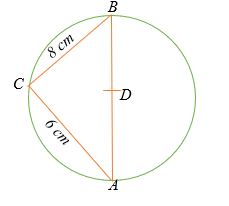

Giải pháp
Theo định lý Thales, tam giác ABC là tam giác vuông có ∠ ACB = 90 °.
Để tìm đường kính của đường tròn, áp dụng định lý Pitago.
CB 2 + AC 2 = AB 2
8 2 + 6 2 = AB 2
64 + 36 = AB 2
100 = AB 2
AB = 10
Do đó, đường kính của hình tròn là 10 cm
Ví dụ 3
Tìm số đo của góc PQR trong hình tròn bên dưới. Giả sử điểm R là tâm của đường tròn.
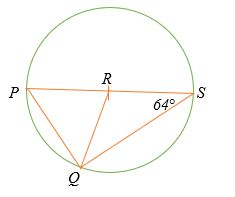

Giải pháp
Tam giác RQS và PQR là các tam giác cân.
∠ RQS = ∠ RSQ = 64 °
Theo định lý Thales, ∠ PQS = 90 °
Vì vậy, ∠ PQR = 90 ° – 64 °
= 26 °
Do đó, số đo của góc PQR là 26 °.
Ví dụ 4
Phát biểu nào sau đây là đúng về định nghĩa của định lý Thales?
Giải pháp
Đáp án đúng là:
Ví dụ 5
Trong vòng tròn hiển thị dưới đây, dòng AB là đường kính của vòng tròn với trung tâm C .
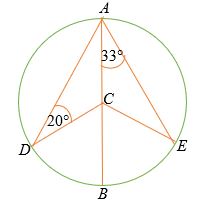

Giải pháp
Cho tam giác ACE là tam giác cân,
∠ CEA = ∠ CAE = 33 °
Vì vậy, ∠ ACE = 180 ° – (33 ° + 33 °)
∠ ACE = 114 °
Nhưng góc trên đường thẳng = 180 °
Do đó, ∠ BCE = 180 ° – 114 °
= 66 °
Tam giác ADC là tam giác cân nên ∠ DAC = 20 °
Theo định lý tổng tam giác, ∠ DCA = 180 ° – (20 ° + 20 °)
∠ DCA = 140 °
∠ DCB = 180 ° – 140 °
= 40 °
Ví dụ 6
Số đo của ∠ ABC là gì?
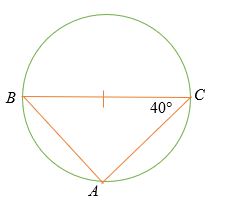

Giải pháp
Định lý Thales phát biểu rằng BAC = 90 °
Và theo định lý tổng tam giác,
∠ ABC + 40 ° + 90 ° = 180 °
∠ ABC = 180 ° – 130 °
= 50 °
Ví dụ 7
Tìm độ dài AB của đường tròn hình bên.
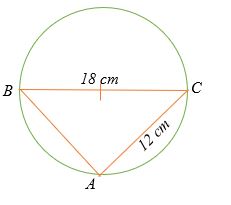

Giải pháp
Tam giác ABC là tam giác vuông.
Áp dụng định lý Pitago để tìm độ dài AB .
AB 2 + 12 2 = 18 2
AB 2 + 144 = 324
AB 2 = 324 – 144
AB 2 = 180
AB = 13,4
Do đó độ dài AB là 13,4 cm.
Trong hình học, không có chủ đề nào là không sử dụng trong thực tế. Do đó, Định lý Thales cũng có một số ứng dụng:
Xem thêm bài viết: