Giải phương trình tuyến tính là gì? Xem xong 5 phút hiểu luôn.

Giải phương trình tuyến tính có nghĩa là tìm nghiệm của một phương trình tuyến tính. Ở đây, các phương pháp giải phương trình tuyến tính được giải thích cho ba loại chính của nó bao gồm phương trình tuyến tính một biến, phương trình tuyến tính hai biến và phương trình tuyến tính ba biến.

Giải phương trình tuyến tính có nghĩa là gì?

Giải một phương trình tuyến tính đề cập đến việc tìm nghiệm của phương trình tuyến tính trong một, hai, ba hoặc biến. Nói một cách dễ hiểu, nghiệm của một phương trình tuyến tính có nghĩa là giá trị hoặc các giá trị của các biến liên quan đến phương trình.

Làm thế nào để giải phương trình tuyến tính?

Có sáu phương pháp chính để giải phương trình tuyến tính. Các phương pháp tìm nghiệm của phương trình tuyến tính là:

• Phương pháp đồ họa
• Phương pháp loại bỏ
• Phương pháp thay thế
• Phương pháp nhân chéo
• hương pháp ma trận
• Phương pháp xác định

Phương pháp đồ thị giải phương trình tuyến tính

Để giải phương trình tuyến tính bằng đồ thị, trước tiên hãy vẽ đồ thị cả hai phương trình trong cùng một hệ tọa độ và kiểm tra giao điểm trong đồ thị. Ví dụ, lấy hai phương trình là 2x + 3y = 9 và x – y = 3.

Bây giờ, để vẽ đồ thị, hãy xem xét x = {0. 1, 2, 3, 4} và giải y. Sau khi thu được (x, y), hãy vẽ các điểm trên biểu đồ. Cần lưu ý rằng bằng cách có nhiều giá trị của x và y hơn sẽ làm cho đồ thị chính xác hơn.

Đồ thị của 2x + 3y = 9 và x – y = 3 sẽ như sau:

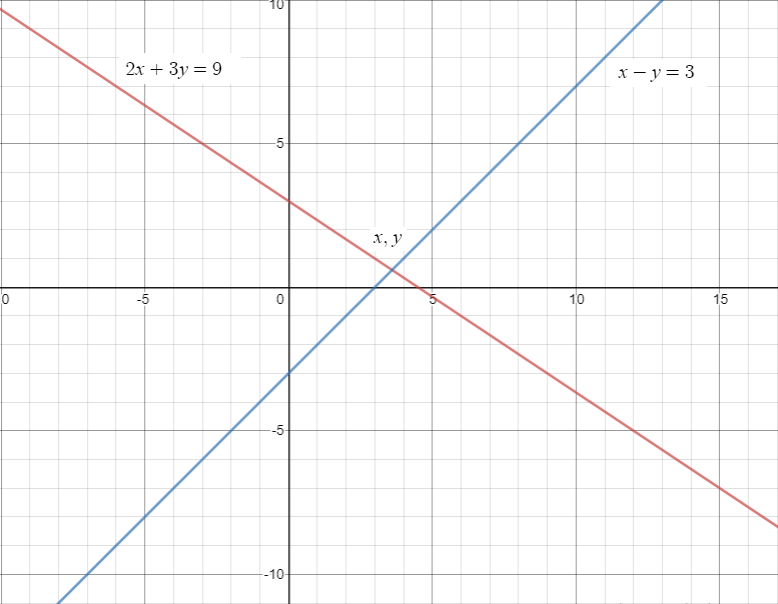
Trong biểu đồ, hãy kiểm tra giao điểm của cả hai đường. Ở đây, nó được đề cập là (x, y). Kiểm tra giá trị của điểm đó và đó sẽ là nghiệm của cả hai phương trình đã cho . Ở đây, giá trị của (x, y) = (3,6, 0,6).

Phương pháp loại bỏ giải phương trình tuyến tính

Trong phương pháp loại trừ , bất kỳ hệ số nào trước tiên được cân bằng và loại bỏ. Sau khi loại bỏ, các phương trình được giải quyết để có được phương trình khác. Dưới đây là ví dụ giải phương trình tuyến tính bằng phương pháp khử để các bạn hiểu rõ hơn.

Hãy xem xét các phương trình tương tự như

2x + 3y = 9 ———– (i)

Và,

x – y = 3 ———– (ii)

Ở đây, nếu phương trình (ii) được nhân với 2, hệ số của “x” sẽ giống nhau và có thể bị trừ đi.

Vì vậy, nhân phương trình (ii) × 2 và sau đó trừ phương trình (i)

2x + 3y = 9

(-)

2x – 2y = 6

_____________

-5y = -3

Hoặc, y = ⅗ = 0,6

Bây giờ, đặt giá trị của y = 0,6 vào phương trình (ii).

Vì vậy, x – 0,6 = 3

Như vậy, x = 3,6

Theo cách này, giá trị của x, y là 3,6 và 0,6.

Phương pháp thay thế giải phương trình tuyến tính

Để giải một phương trình tuyến tính bằng phương pháp thay thế , trước tiên, tách giá trị của một biến khỏi bất kỳ phương trình nào. Sau đó, thay giá trị của biến cô lập trong phương trình thứ hai và giải nó. Lấy các phương trình tương tự một lần nữa làm ví dụ.

Xem xét,

2x + 3y = 9 ———– (i)

Và,

x – y = 3 ———– (ii)

Bây giờ, hãy xem xét phương trình (ii) và tách biến “x”.

Vì vậy, phương trình (ii) trở thành,

x = 3 + y.

Bây giờ, thay giá trị của x vào phương trình (i). Vì vậy, phương trình (i) sẽ là-

2x + 3y = 9

⇒ 2 (3 + y) + 3y = 9

⇒ 6 + 2y + 3y = 9

Hoặc, y = ⅗ = 0,6

Bây giờ, hãy thay thế giá trị “y” trong phương trình (ii).

x – y = 3

⇒ x = 3 + 0,6

Hoặc, x = 3,6

Như vậy, (x, y) = (3,6, 0,6).

Phép nhân chéo phương pháp giải phương trình tuyến tính

Phương trình tuyến tính có thể được giải quyết dễ dàng bằng cách sử dụng phương pháp nhân chéo. Trong phương pháp này, kỹ thuật nhân chéo được sử dụng để đơn giản hóa giải pháp. Đối với phương pháp nhân chéo để giải phương trình 2 biến, công thức được sử dụng là:

x / (b ₁ c ₂ – b ₂ c ₁ ) = y / (c ₁ a ₂ – c ₂ a ₁ ) = 1 / (b ₂ a ₁ – b ₁ a ₂ )

Ví dụ, hãy xem xét các phương trình

2x + 3y = 9 ———– (i)

Và,

x – y = 3 ———– (ii)

Đây,

a ₁ = 2, b ₁ = 3, c ₁ = -9

a ₂ = 1, b ₂ = -1, c ₂ = -3

Bây giờ, hãy giải quyết bằng cách sử dụng công thức nói trên.

x = (b ₁ c ₂ – b ₂ c ₁ ) / (b ₂ a ₁ – b ₁ a ₂ )

Đặt giá trị tương ứng mà chúng tôi nhận được,

x = 18/5 = 3,6

Tương tự, giải cho y.

y = (c ₁ a ₂ – c ₂ a ₁ ) / (b ₂ a ₁ – b ₁ a ₂ )

Vì vậy, y = ⅗ = 0,6

Phương pháp ma trận giải phương trình tuyến tính

Phương trình tuyến tính cũng có thể được giải bằng phương pháp ma trận. Phương pháp này rất hữu ích để giải các phương trình tuyến tính trong hai hoặc ba biến. Xét ba phương trình là:

a ₁ x + a ₂ y + a ₃ z = d ₁

b ₁ x + b ₂ y + b ₃ z = d ₂

c ₁ x + c ₂ y + c ₃ z = d ₃

Các phương trình này có thể được viết dưới dạng:

⇒ AX = B ————- (i)

Ở đây, ma trận A, ma trận B và ma trận X là:

Bây giờ, nhân (i) với A ^-1 để được:

A ⁻¹ AX = A ⁻¹ B ⇒ IX = A ⁻¹ B

⇒ X = A ⁻¹ B

Phương pháp xác định giải phương trình tuyến tính (Quy tắc Cramer)

Phương pháp xác định có thể được sử dụng để giải các phương trình tuyến tính hai hoặc ba biến một cách dễ dàng. Đối với hai biến và ba biến của phương trình tuyến tính, quy trình như sau.

Đối với phương trình tuyến tính trong hai biến:

x = Δ ₁ / Δ,

y = Δ ₂ / Δ

Hoặc, x = (b ₁ c ₂ – b ₂ c ₁ ) / (b ₂ a ₁ – b ₁ a ₂ ) và y = (c ₁ a ₂ – c ₂ a ₁ ) / (b ₂ a ₁ – b ₁ a ₂ )

Đây,

Đối với phương trình tuyến tính trong ba biến:

Các phương pháp giải phương trình tuyến tính trong một biến

Giải một phương trình tuyến tính với một biến cực kỳ dễ dàng và nhanh chóng. Để giải hai phương trình bất kỳ chỉ có 1 biến, hãy đưa tất cả các số hạng biến ở một bên và các hằng số ở bên kia. Phương pháp đồ thị cũng có thể được sử dụng trong đó giao điểm của đường thẳng với trục x hoặc trục y sẽ cho nghiệm của phương trình.

Ví dụ, hãy xem xét phương trình 2x + 4 + 7 = 4x – 3 + x

Ở đây, hãy kết hợp các thuật ngữ “x” và đưa chúng về một phía.

Vì thế,

5x – 2x = 14

Hoặc, x = 14/3

Phương pháp giải phương trình tuyến tính trong hai biến

Để giải một phương trình tuyến tính hai biến , có thể sử dụng bất kỳ phương pháp nào nêu trên như phương pháp đồ thị, phương pháp loại trừ, phương pháp thay thế, phương pháp nhân chéo, phương pháp ma trận, phương pháp định thức.

Phương pháp giải phương trình tuyến tính trong ba biến trở lên

Để giải bất phương trình nào có ba biến trở lên, phương pháp đồ thị, loại trừ và thay thế là không khả thi. Để giải một phương trình ba biến, phương pháp nhân chéo là phương pháp được ưu tiên hơn cả. Ma trận chẵn quy tắc Cramer cực kỳ hữu ích để giải các phương trình có 3 biến trở lên.