Hình tam giác vuông đặc biệt – Giải thích & Ví dụ hay nhất

Bây giờ bạn đã biết một tam giác là một đa giác hai chiều có 3 cạnh , 3 góc và 3 đỉnh . Trong bài này, chúng ta sẽ cùng nhau tìm hiểu các dạng tam giác khác được gọi là tam giác vuông đặc biệt. Trước khi chúng ta có thể bắt đầu, chúng ta hãy nhớ lại về một tam giác vuông.

Một tam giác vuông là gì?

Thuật ngữ ” phải ” dùng để chỉ từ ” trực tràng ” trong tiếng Latinh có nghĩa là ngay thẳng. Do đó, tam giác vuông là tam giác có một góc bằng 90 độ ( góc vuông ). Hình tam giác vuông được biểu thị bằng một hộp ở vị trí của góc vuông.

Cạnh dài nhất của tam giác vuông nằm trên cạnh đối diện của góc vuông được gọi là cạnh huyền. Hai cạnh còn lại của tam giác được gọi là chân. Chân ngang là chân trụ và chân thẳng đứng là chiều cao của tam giác vuông.

Hình minh họa:

Tam giác phải Đặc biệt là gì?

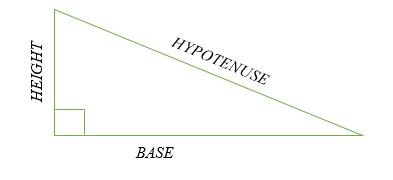
Tam giác vuông đặc biệt là những tam giác có các cạnh theo một tỷ lệ cụ thể, được gọi là Tam giác Pitago. Trong hình học, Định lý Pitago là một phát biểu chỉ ra mối quan hệ của các cạnh của một tam giác vuông.

Phương trình của một tam giác vuông được cho bởi a ²  + b ²  = c ² , trong đó a hoặc b là chiều cao và đáy của tam giác và c là cạnh huyền. Bằng cách sử dụng Định lý Pitago, quá trình tìm cạnh bị thiếu của một tam giác khá đơn giản và dễ dàng.

Hai tam giác vuông đặc biệt bao gồm:

• 45 °; 45 °; Hình tam giác 90 °
• 30 °; 60 °; Hình tam giác 90 °

Chúng ta hãy cùng tìm hiểu sơ lược về những hình tam giác vuông đặc biệt này như chúng ta sẽ thấy chúng một cách chi tiết trong các bài viết tiếp theo.

45 °; 45 °; Hình tam giác 90 °

Đây là một tam giác vuông đặc biệt có số đo các góc là 45 °, 45 ° và 90 °. Tỉ số giữa chiều cao và cạnh huyền của tam giác này là 1: 1: √2.

Cơ sở: Chiều cao: Hypotenuse = x: x: x√2 = 1: 1: √2.

Nói cách khác, 45 °; 45 °; Tam giác 90 ° cũng có thể là tam giác cân. Tam giác cân là tam giác có độ dài hai cạnh bằng nhau và hai góc của nó bằng nhau.

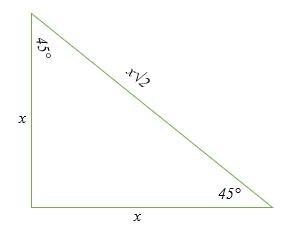
Bằng cách sử dụng phương trình của tam giác vuông a ²  + b ²  = c ² , chúng ta có thể tính cạnh huyền của, a 45 °; 45 °; 90 ° tam giác như sau:

Kể từ, một 45 °; 45 °; Tam giác 90 ° cũng là tam giác cân;

cho a = b = x;

x ² + x ² = 2x ²

Tìm căn bậc hai của mỗi số hạng trong phương trình

√x ² + √x ² = √ (2x ² )

x + x = x √2

Do đó, cạnh huyền của một góc 45 °; 45 °; 90 ° tam giác là x √2

30 °; 60 °; Hình tam giác 90 °

Đây là một dạng đặc biệt của tam giác vuông có các góc là 30 °; 60 °; 90 °. Tỉ số độ dài các cạnh là x: x√3: 2x.

Làm thế nào để giải các tam giác vuông đặc biệt?

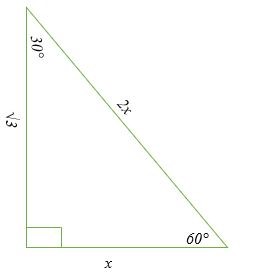
Giải các tam giác vuông đặc biệt có nghĩa là tìm độ dài còn thiếu của các cạnh. Thay vì sử dụng Định lý Pitago, chúng ta có thể chỉ cần sử dụng các tỷ lệ tam giác vuông đặc biệt để thực hiện các phép tính.

Hãy làm một vài ví dụ.

ví dụ 1

Các cạnh dài hơn của một 30 °; 60 °; 90 ° tam giác vuông được cho bởi 8√3 cm. Số đo chiều cao và cạnh huyền của nó là gì?

Giải pháp

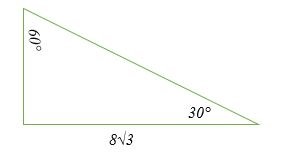
Cách tốt nhất để giải quyết những vấn đề kiểu này là vẽ phác các hình tam giác:

Tỷ lệ của một 30 °; 60 °; Tam giác vuông 90 ° là x: x√3: 2x. Trong trường hợp này, x và x√3 lần lượt là cạnh ngắn hơn và dài hơn trong khi 2x là cạnh huyền.

Do đó, x√3 = 8√3 cm

Bình phương cả hai vế của phương trình.

⇒ (x√3) ² = (8√3) ²

⇒ 3x ² = 64 * 3

⇒ x ² = 64

Tìm bình phương của cả hai cạnh.

√x ² = √64

x = 8cm

Người thay thế.

2x = 2 * 8 = 16cm.

Do đó, cạnh ngắn hơn là 8cm và cạnh huyền là 16cm.

Ví dụ 2

Cạnh huyền của một góc 45 °; 45 °; 90 ° tam giác là 6√2 mm. Tính độ dài của cơ sở và chiều cao của nó.

Giải pháp

Tỷ lệ 45 °; 45 °; 90 ° tam giác là x: x: x√2. Vì vậy chúng tôi có;

⇒x√2 = 6√2 mm

Bình phương cả hai vế của phương trình.

⇒ (x√2) ² = (6√2) ² mm

⇒ 2x ² = 36 * 2

⇒ 2x ² = 72

x ² = 36

Tìm căn bậc hai.

x = 6mm

Thay thế x = 6mm theo tỷ lệ.

Do đó, đáy và chiều cao của tam giác vuông mỗi cạnh là 6mm.

Ví dụ 3

Nếu đường chéo của một tam giác vuông là 8 cm, hãy tìm độ dài hai cạnh còn lại của tam giác đã cho rằng một trong các góc của nó là 30 độ.

Giải pháp

Đây phải là một tam giác 30 ° -60 ° -90 °. Do đó, ta sử dụng tỷ lệ x: x√3: 2x.

Cho trước, đường chéo = cạnh huyền = 8cm.

⇒2x = 8 cm

⇒ x = 4cm

Người thay thế.

x√3 = 4√3 cm

Cạnh ngắn hơn của tam giác vuông là 4cm và cạnh dài hơn là 4√3 cm

Ví dụ 4

Tìm cạnh huyền của một tam giác 30 ° – 60 ° – 90 ° có cạnh dài hơn là 6 inch.

Giải pháp

Tỉ lệ = x: x√3: 2x.

⇒ x√3 = 6 inch.

Hình vuông cả hai bên

⇒ (x√3) ² = 36

⇒ 3x ² = 36

x ² = 12

x = 2√3 inch.

Ví dụ 5

Thang dựa vào tường tạo với mặt đất một góc 30 độ. Nếu chiều dài của cái thang là 9 m, hãy tìm;

1. Chiều cao của bức tường.
2. Tính độ dài giữa chân thang và tường.

Giải pháp

Cho rằng, một góc là 30 độ, thì đây phải là một tam giác vuông 60 ° – 60 ° – 90 °.

Tỉ lệ = x: x√3: 2x.

⇒ 2x = 9

⇒ x = 9/2

= 4,5

Người thay thế.

1. Chiều cao của bức tường = 4,5m
2. x√3 = 4,5√3m

Ví dụ 6:

Độ dài cạnh huyền và cạnh kia của tam giác vuông lần lượt là 15 cm và 12 cm. Tìm độ dài của cạnh còn lại.

Giải pháp:

Kiểm tra xem tỷ lệ các chiều dài có phù hợp với tỷ lệ 3n: 4n: 5n hay không.

? : 12: 15 =? : 4 (3): 5 (3)

Có, đây là tam giác 3-4-5

Bây giờ, hãy tính cạnh thứ ba

Đối với n = 3,

3n = 3 × 3 = 9

Do đó, chiều dài của cạnh còn lại là 9 cm.

Ví dụ 7:

Nếu hai cạnh của một tam giác vuông là 6 ft và 8 ft, hãy tìm độ dài cạnh huyền.

Giải pháp:

Kiểm tra xem tỷ lệ có phù hợp với 3n: 4n: 5n không

6: 8 😕 = 3 (2): 4 (2) 😕

Có, đây là tam giác 3-4-5

Bây giờ, hãy tính độ dài của cạnh huyền

Đối với n = 2,

5n = 5 × 2 = 10

Do đó, chiều dài của cạnh huyền là 10 ft.

Ví dụ 8:

Độ dài cạnh huyền của một tam giác vuông với hai cạnh của nó là 4 inch và 4√3 inch.

Giải pháp:

Kiểm tra xem tỷ lệ độ dài có phù hợp với tỷ lệ n: n√3: 2n hay không

4: 4√3:? = n: n√3: 2n

Đúng, đây là tam giác 30-60-90 với n = 4

Bây giờ, hãy tìm chiều dài của cạnh thứ ba.

2n = 2 × 4 = 8

Do đó, chiều dài của cạnh huyền là 8 inch.

Xem thêm:

Định lý Pitago và những kiến thức cho người mới nhập môn

Cách học định lý Tam giác Sum hiệu quả nhất hiện nay

Câu hỏi thực hành

1. Nếu độ dài một cạnh của tam giác đều là 15 m thì độ dài đường cao của tam giác đó là bao nhiêu?
2. Nếu độ dài đường chéo của hình vuông là 10 đơn vị thì diện tích của hình vuông là bao nhiêu?
3. Nếu đường cao của tam giác đều là 22 cm thì độ dài cạnh của tam giác đều là bao nhiêu?
4. Nếu hai cạnh ngắn hơn của một tam giác vuông cân, mỗi cạnh là 3 cm thì độ dài của cạnh thứ ba là bao nhiêu?
5. Nếu cạnh huyền của Tam giác 30 ° -60 ° -90 ° là 10√3 / 3, hãy tìm độ dài các cạnh ngắn hơn của nó.