Định lý Góc ngoài đơn giản dễ hiểu nhất 2021

Định lý Góc ngoài – Giải thích & Ví dụ

Vì vậy, chúng ta đều biết rằng một tam giác là một hình có 3 cạnh với ba góc nội tiếp. Nhưng tồn tại các góc khác bên ngoài tam giác mà chúng ta gọi là các góc bên ngoài .

Ta biết rằng trong một tam giác, tổng của cả ba góc trong luôn bằng 180 độ.

Tương tự, đặc tính này cũng đúng với các góc bên ngoài. Ngoài ra, mỗi góc bên trong của một tam giác lớn hơn 0 độ nhưng nhỏ hơn 180 độ. Tương tự đối với các góc bên ngoài.

Trong bài viết này, chúng ta sẽ tìm hiểu về:

• Định lý góc ngoài tam giác,
• các góc bên ngoài của một tam giác và,
• làm thế nào để tìm góc bên ngoài chưa biết của một tam giác.

Góc bên ngoài của một tam giác là gì?

Góc ngoài của tam giác là góc được tạo thành giữa một cạnh của tam giác và phần kéo dài của cạnh liền kề của nó.

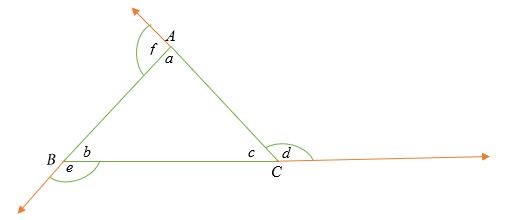
Trong hình minh họa trên, các góc trong của tam giác ABC là a, b, c và các góc bên ngoài là d, e và f. Các góc bên trong và bên ngoài liền kề là các góc bổ sung.

Nói cách khác, tổng của mỗi góc bên trong và góc bên ngoài liền kề của nó bằng 180 độ (đường thẳng).

Định lý góc ngoại thất tam giác

Định lý góc bên ngoài phát biểu rằng số đo của mỗi góc bên ngoài của một tam giác bằng tổng của các góc bên trong đối diện và không kề bên.

Hãy nhớ rằng hai góc bên trong không liền kề, đối diện với góc bên ngoài đôi khi được gọi là góc bên trong từ xa.

Ví dụ, trong tam giác ABC trên;

⇒ d = b + a

⇒ e = a + c

⇒ f = b + c

Tính chất của các góc bên ngoài

• Góc bên ngoài của một tam giác bằng tổng của hai góc bên trong đối diện.
• Tổng của góc ngoại thất và góc nội thất bằng 180 độ.

⇒ c + d = 180 °

⇒ a + f = 180 °

⇒ b + e = 180 °

• Tất cả các góc bên ngoài của hình tam giác cộng lại tối đa 360 °.

Bằng chứng: 

⇒ d + e + f = b + a + a + c + b + c

⇒ d + e + f = 2a + 2b + 2c

= 2 (a + b + c)

Nhưng, theo định lý tổng góc tam giác,

a + b + c = 180 độ

Do đó, ⇒ d + e + f = 2 (180 °)

= 360 °

Làm thế nào để tìm các góc bên ngoài của một tam giác?

Quy tắc tìm các góc bên ngoài của một tam giác khá giống với các quy tắc tìm các góc trong của một tam giác. Đó là bởi vì bất cứ nơi nào có góc bên ngoài, ở đó tồn tại một góc bên trong và cả hai góc này cộng lại với nhau lên đến 180 độ.

Chúng ta hãy xem xét một vài vấn đề ví dụ.

ví dụ 1

Cho rằng đối với một tam giác, hai góc trong 25 ° và (x + 15) ° không kề với một góc ngoài (3x – 10) °, hãy tìm giá trị của x.

Giải pháp

Áp dụng định lý góc ngoại tiếp tam giác:

⇒ (3x – 10) = (25) + (x + 15)

⇒ (3x – 10) = (25) + (x +15)

⇒ 3x −10 = x + 40

⇒ 3x – 10 = x + 40

⇒ 3x = x + 50

⇒ 3x = x + 50

⇒ 2x = 50

x = 25

Do đó, x = 25 °

Thay giá trị của x vào ba phương trình.

⇒ (3x – 10) = 3 (25 °) – 10 °

= (75 – 10) ° = 65 °

⇒ (x + 15) = (25 + 15) ° = 40 °

Do đó, các góc là 25 °, 40 ° và 65 °.

Ví dụ 2

Tính giá trị của  x  và  y  trong tam giác sau.

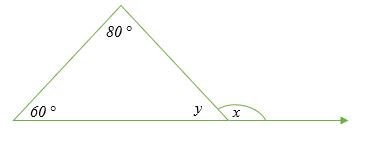
Giải pháp

Rõ ràng từ hình vẽ rằng y là góc bên trong và x là góc bên ngoài.

Theo định lý góc ngoại tiếp tam giác.

⇒ x = 60 ° + 80 °

x = 140 °

Tổng của góc bên ngoài và góc bên trong bằng 180 độ (thuộc tính của các góc bên ngoài). Vì vậy chúng tôi có;

⇒ y + x = 180 °

⇒ 140 ° + y = 180 °

trừ 140 ° cho cả hai bên.

⇒ y = 180 ° – 140 °

y = 40 °

Do đó, giá trị của x và y lần lượt là 140 ° và 40 °.

Xem thêm:

Diện tích tam giác – Giải thích và ví dụ chi tiết dễ hiểu nhất

Định lý chân Hypotenuse – Giải thích & Ví dụ đơn giản nhất

Ví dụ 3

Góc bên ngoài của một tam giác là 120 °. Tìm giá trị của x nếu các góc trong không liền kề đối diện là (4x + 40) ° và 60 °.

Giải pháp

Góc ngoại thất = tổng của hai góc nội thất đối diện không kề nhau.

⇒120 ° = 4x + 40 + 60

Đơn giản hóa.

⇒ 120 ° = 4x + 100 °

Trừ 120 ° cho cả hai bên.

⇒ 120 ° – 100 ° = 4x + 100 ° – 100 °

⇒ 20 ° = 4x

Chia cả hai bên để có được,

x = 5 °

Do đó, giá trị của x là 5 độ.

Xác minh câu trả lời bằng cách thay thế.

120 ° = 4x + 40 + 60

120 ° = 4 ° (5) + 40 ° + 60 °

120 ° = 120 ° (RHS = LHS)

Ví dụ 4

Xác định giá trị của x và y trong hình bên.

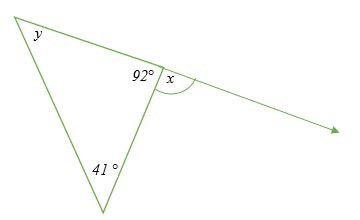
Giải pháp

Tổng các góc bên trong = 180 độ

y + 41 ° + 92 ° = 180 °

Đơn giản hóa.

y + 133 ° = 180 °

trừ 133 ° cho cả hai bên.

y = 180 ° – 133 °

y = 47 °

Áp dụng định lý góc ngoại tiếp tam giác.

x = 41 ° + 47 °

x = 88 °

Do đó, giá trị của x và y lần lượt là 88 ° và 47 °.