Contents
Hằng số đàn hồi
Hằng số đàn hồi là những hằng số xác định biến dạng được tạo ra bởi một hệ ứng suất nhất định tác dụng lên vật liệu.
- Các hằng số đàn hồi được sử dụng để xác định biến dạng kỹ thuật về mặt lý thuyết.
- Chúng được sử dụng để xác định mối quan hệ giữa ứng suất kỹ thuật và ứng suất kỹ thuật.
- Đối với một vật liệu đồng chất và đẳng hướng, số hằng số đàn hồi là 4.
Các loại hằng số đàn hồi
- Môđun của Young hoặc môđun của Độ đàn hồi (E)
- Mô đun cắt hoặc mô đun độ cứng (G)
- Mô đun số lượng lớn (K)
- Tỷ lệ Poisson (µ)
Trong bài viết này, chúng tôi chỉ thảo luận về loại đầu tiên là mô đun Young hoặc mô đun đàn hồi (E)
Mối quan hệ giữa các hằng số co giãn
- E = 2G (1+ µ)
- E = 3 K (1-2µ)
- – E = 9 K G / G + 3 K
Hy vọng bạn đã hiểu mối quan hệ giữa mô-đun Young và mô-đun số lượng lớn k và mô-đun cứng
Giá trị của bất kỳ hằng số nào luôn lớn hơn hoặc bằng 0. Dấu âm chỉ phương.
Định nghĩa Mô đun đàn hồi
Theo định luật Hooke, đến giới hạn tỷ lệ, “đối với biến dạng nhỏ, ứng suất tỷ lệ thuận với biến dạng.”
Về mặt toán học, Định luật Hooke được biểu thị như sau:
Căng thẳng α Strain
σ = E ε
Trong công thức như đã đề cập ở trên, “E” được gọi là Mô đun đàn hồi.
σ là ứng suất, và ε biểu thị căng thẳng.
Chúng ta có thể viết biểu thức cho Môđun co giãn bằng cách sử dụng phương trình trên dưới dạng,
E = (F * L) / (A * δL)
Vì vậy, chúng ta có thể định nghĩa mô đun đàn hồi là tỷ số giữa ứng suất pháp và biến dạng dọc.
Đơn vị của mô đun đàn hồi
Đơn vị của ứng suất thông thường là Pascal, và biến dạng dọc không có đơn vị. Vì biến dạng dọc là tỷ số thay đổi chiều dài so với chiều dài ban đầu. Vì vậy, đơn vị của Môđun của Độ co giãn cũng giống như của Ứng suất, và nó là Pascal (Pa). Chúng tôi sử dụng phổ biến nhất Megapascals (MPa) và Gigapascals (GPa) để đo mô-đun Độ co giãn.
1 MPa = Pa
1 GPa = Pa
Làm thế nào để đo Mô-đun đàn hồi của Trẻ hoặc Mô-đun đàn hồi?
Chúng ta hãy lấy một thanh làm bằng vật liệu dẻo là thép nhẹ. Bây giờ hãy thực hiện kiểm tra độ căng trên máy kiểm tra Universal. Sau khi kiểm tra lực căng khi chúng ta vẽ biểu đồ ứng suất-biến dạng, thì chúng ta sẽ có được đường cong như dưới đây.
Từ đường cong, chúng ta thấy rằng từ điểm O đến B, miền là một miền đàn hồi. Sau đó, biến dạng dẻo bắt đầu. Điểm A trong đường cong cho thấy giới hạn của tỷ lệ. Đối với đường cong này, chúng ta có thể viết giá trị của Môđun đàn hồi (E) bằng độ dốc của đường cong ứng suất-biến dạng lên đến A.
Nếu giá trị của E tăng lên, thì biến dạng dọc giảm, điều đó có nghĩa là sự thay đổi chiều dài giảm.
Dưới đây là một số giá trị của E đối với các vật liệu được sử dụng phổ biến nhất.
- Thép nhẹ- E = 200 GPa
- Gang E = 100 GPa
- Nhôm E = 200/3 GPa
Xác định mô đun Young của vật liệu làm dây
Hãy bố trí thí nghiệm như hình bên để xác định giá trị của môđun Young của vật liệu làm dây chịu lực căng.
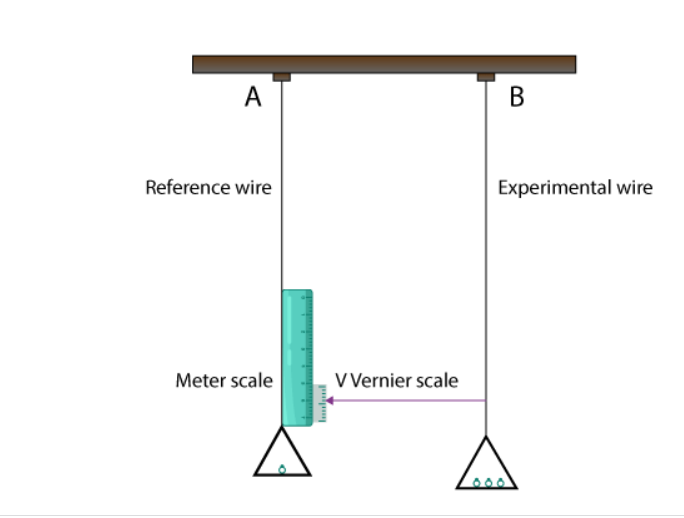

Lấy hai sợi dây thẳng giống nhau (cùng chiều dài và bán kính bằng nhau) A và B. Bây giờ cố định đầu của nó từ một giá đỡ cố định, cứng. Dây A là dây chuẩn, nó mang một thước chính M và một cái chảo để đặt quả nặng. Dây B là dây thí nghiệm. Nó cũng mang một cái chảo trong đó các trọng lượng đã biết được đặt vào. Ở dưới cùng của dây, B gắn một thang đo V vernier.
Bây giờ, sau khi đặt quả nặng vào chảo nối với B, nó tác dụng một lực hướng xuống. Khi chịu tác dụng của lực hướng xuống này (ứng suất kéo), dây B bị kéo căng. Độ giãn dài (tăng chiều dài) của dây B được đo bằng thang đo vernier. Dây tham chiếu A được sử dụng để bù cho bất kỳ thay đổi nào về chiều dài có thể xảy ra do thay đổi nhiệt độ phòng. Ban đầu, cho một tải nhỏ vào cả hai dây A và B để cả hai đều thẳng và lấy số đọc và Vernier. Bây giờ tăng dần tải trong dây B và lưu ý đọc vernier. Sự khác biệt giữa hai giá trị đọc vernier này cho thấy sự thay đổi về chiều dài được tạo ra trong dây.
Gọi bán kính và chiều dài ban đầu của dây B lần lượt là r và L,
Khi đó, diện tích mặt cắt ngang của dây sẽ là pr 2
Gọi M là khối lượng gây ra độ dãn dài ĐL trong dây B.
Khi đó lực tác dụng bằng Mg, trong đó g là gia tốc trọng trường.
Từ phương trình,
E = ( F / A ) / (D L / L )
= ( F × L ) / ( A × D L)
Môđun Young của vật liệu của dây thí nghiệm B được cho bởi;
Y = σ / ε
Y = (F / A) / (ΔL / L)
Y = (F × L) / (A × ΔL)
Y = (Mg × L) / (A × ΔL)
Sự thật thú vị về Mô đun đàn hồi
- Modulus of Elasticity và Young’s Modulus đều giống nhau. Môđun đàn hồi là không đổi.
- Robert Hooke giới thiệu nó. Robert Hooke (1635 – 1703) là Nhà khoa học đầu tiên nghiên cứu về Cơ học ứng dụng.
- Trong khi mô đun của Young được Thomas Young ký hiệu là “E” vào năm 1807. Nó được giải thích trong “Khóa học các bài giảng về triết học tự nhiên và nghệ thuật cơ khí” được viết bởi Thomas Young. Anh ấy đã nghiên cứu chi tiết về Đặc tính đàn hồi.
- Theo Robert Hook, giá trị của E phụ thuộc vào cả hình dạng và vật liệu đang được xem xét. Để tìm ra giá trị của E, cần phải kiểm tra vật lý đối với bất kỳ thành phần mới nào.
- Thomas Young nói rằng giá trị của E chỉ phụ thuộc vào vật liệu chứ không phụ thuộc vào hình học của nó ”. Vì vậy, ông đã thực hiện một cuộc cách mạng trong các chiến lược kỹ thuật.
- Một miếng cao su nhỏ và miếng cao su lớn có cùng môđun đàn hồi.
- Mô đun đàn hồi còn được gọi là mô đun kéo hoặc mô đun đàn hồi.
- Nó là thuộc tính cơ bản của mọi vật chất không thể thay đổi được. Tuy nhiên, nó phụ thuộc vào nhiệt độ và áp suất.
- Mô đun đàn hồi là thước đo độ cứng của vật liệu. Nói cách khác, nó là thước đo mức độ dễ dàng của bất kỳ vật liệu nào có thể bị uốn cong hoặc kéo dài.
- Nó là độ dốc của biểu đồ ứng suất và biến dạng đến giới hạn tỷ lệ thuận.
Ứng dụng của nó là gì?
- Nó được sử dụng trong kỹ thuật cũng như khoa học y tế.
- Bạn có thể sử dụng mô-đun đàn hồi để tính xem một vật liệu sẽ kéo căng bao nhiêu và cũng như bao nhiêu thế năng sẽ được tích trữ.
- Mô đun đàn hồi cho phép bạn xác định cách một vật liệu nhất định sẽ phản ứng với Ứng suất.
- Mô đun đàn hồi được sử dụng để đặc trưng cho các vật liệu sinh học như sụn và xương.
Xem thêm: