Vecto pháp tuyến và vecto chỉ phương

Dưới đây là Vecto pháp tuyến và vecto chỉ phương của mặt phẳng trong không gian Oxyz, các bạn có thể tham khảo dưới đây 

Vecto pháp tuyến và vecto chỉ phương

Vecto pháp tuyến của mặt phẳng trong không gian Oxyz

Định nghĩa: nếu như có một vecto n→≠0→ nhưng vuông góc với mặt phẳng (Q) cho trước thì ta nói n→ là vecto pháp tuyến của mặt phẳng (Q).

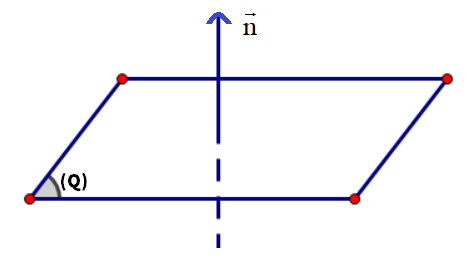
Vecto pháp tuyến của mặt phẳng (Q)

Theo định nghĩa trên thì:

• Mỗi mặt phẳng sẽ có vô kể vecto pháp tuyến nhưng mà các vecto này luôn cùng phương với nhau.
• giả dụ ta biết được vecto pháp tuyến và một điểm nằm trong mặt phẳng thì ta hoàn toàn xác định được phương trình mặt phẳng đó.
• Ngoài n→≠0→ là vecto pháp tuyến của mặt phẳng (Q), vecto này còn là vecto pháp tuyến của vô kể mặt phẳng khác, các mặt phẳng này song song với mặt phẳng (P).

nếu như biết phương trình mặt phẳng (P): Ax + By + Cz + D = 0 thì ta chỉ ngay được vecto pháp tuyến của (P) là n→ = ( A; B; C)

Ví dụ: Cho phương trình mặt phẳng (α): 2x + 3y – z + 5 = 0. Chọn đáp án đúng khi nói về vecto chỉ phương của (α)?

A. n→ = ( – 2; 3; 5)

B. n→ = ( 2; 3; 5)

C. n→ = ( 2; 3; – 1)

D. n→ = ( 3; – 1; 5)

Lời giải

Dựa theo lý thuyết trên, ta dễ dàng chỉ ra được vecto pháp tuyến của (α) là n→ = ( 2; 3; – 1)

Vecto chỉ phương của mặt phẳng

Định nghĩa: giả dụ có một vecto u→≠0→ nhưng mà đồng thời hoặc nằm trong mặt phẳng (Q) cho trước thì ta nói u→ là vecto chỉ phương của mặt phẳng (Q).

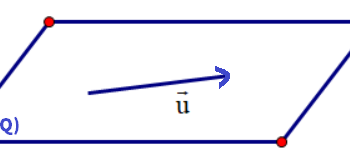
Từ khái niệm trên cho ta thấy:

• Mỗi mặt phẳng sẽ có ti tỉ vecto chỉ phương.
• Các vecto chỉ phương này song song vuông góc với vecto pháp tuyến của mặt phẳng (Q).
• Theo tri thức tích có hướng thì nếu biết 2 vecto chỉ phương của (Q) (hai vecto này không cùng phương) thì ta tìm được vecto pháp tuyến

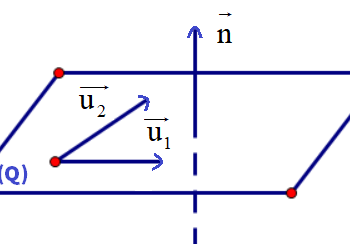
Ví dụ: Một mặt phẳng (Q) cho trước biết cặp vecto chỉ phương lần lượt là u1→ = ( 1; 2; – 1) và u2→ = ( – 1; 0; 1). Hãy tìm vecto pháp tuyến của mặt phẳng (Q).

Lời giải

Dựa theo lý thuyết trên, vecto pháp tuyến chính bằng tích có hướng của 2 vecto chỉ phương mà đề bài cho

n→=[n1−→,n2−→] =(∣∣∣2–101∣∣∣;∣∣∣–111–1∣∣∣;∣∣∣12–10∣∣∣) = ( 2; 0; 2)

Ta thấy n→ = ( 1; 0; 1) cũng là vecto pháp tuyến của mặt phẳng (Q)

Trên đây là những san sớt về vecto pháp tuyến của mặt phẳng. chờ đợi rằng bài viết này đã giúp ích được cho bạn trong quá trình học tốt hình học lớp 12. Đừng quên hãy theo dõi tintuctuyensinh để đón xem những chủ đề hay tiếp theo nhé