Yếu tố theo nhóm – Làm thế nào để nhân tử của tam thức bằng cách nhóm?

Yếu tố theo nhóm – Phương pháp & Ví dụ

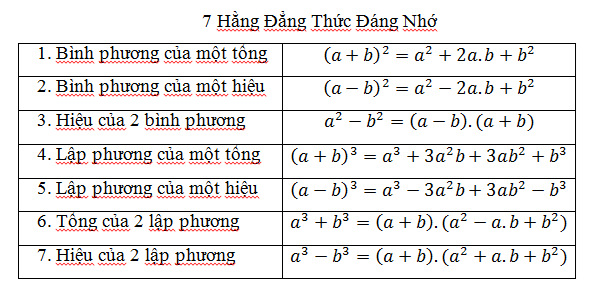
Bây giờ bạn đã học cách nhân tử đa thức bằng cách sử dụng các phương pháp khác nhau như; Hệ số chung lớn nhất (GCF, Tổng hoặc hiệu số của hai hình lập phương; Hiệu số trong phương pháp hai bình phương; và phương pháp Tam thức.

Bạn thấy phương pháp nào đơn giản nhất trong số này?

Tôi có thể nói rằng tất cả các phương pháp tính đa thức tính thừa này đều dễ dàng như ABC, chỉ khi chúng được áp dụng đúng cách.

Trong bài viết này, chúng ta sẽ tìm hiểu một phương pháp đơn giản khác được gọi là bao thanh toán bằng cách nhóm, nhưng trước khi đi vào chủ đề bao thanh toán bằng cách nhóm, chúng ta hãy thảo luận về tính nhân tử của một đa thức.

Đa thức là một biểu thức đại số có một hoặc nhiều số hạng, trong đó hằng số và biến số được phân tách bằng một phép cộng hoặc một dấu trừ.

Dạng tổng quát của đa thức là ax ⁿ  + bx ^n-1  + cx ^n-2  +…. + kx + l, trong đó mỗi biến có một hằng số đi kèm như hệ số của nó. Các loại đa thức khác nhau bao gồm; nhị thức, tam thức và tứ thức.

Ví dụ về đa thức là; 12x + 15, 6x ²  + 3xy – 2ax – ay, 6x ²  + 3x + 20x + 10, v.v.

Làm thế nào để nhân tố theo nhóm?

Nhân tố theo Nhóm hữu ích khi không có nhân tử chung giữa các thuật ngữ và bạn chia biểu thức thành hai cặp và nhân tử riêng cho từng thuật ngữ.

Tính nhân tử đa thức  là phép toán ngược lại của phép nhân vì nó biểu thị một đa thức là tích của hai hay nhiều thừa số. Các đa thức có thể được tính theo nhân tử để tìm ra gốc hoặc nghiệm của một biểu thức.

Làm thế nào để nhân tử của tam thức bằng cách nhóm?

Để nhân tử một tam thức có dạng ax ²  + bx + c bằng cách nhóm, ta thực hiện quy trình như hình dưới đây:

• Tìm tích của hệ số hàng đầu “a” và hằng số “c”.

⟹ a * c = ac

• Tìm các hệ số của “ac” cộng vào hệ số “b”.
• Viết lại bx dưới dạng tổng hoặc hiệu của các thừa số của ac cộng với b.

⟹ ax ² + bx + c = ax ² + (a + c) x + c

⟹ ax ² + ax + cx + c

• Bây giờ tính theo nhóm.

⟹ ax (x + 1) + c (x + 1)

⟹ (ax + c) (x + 1)

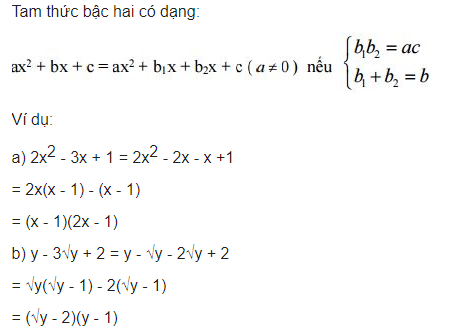
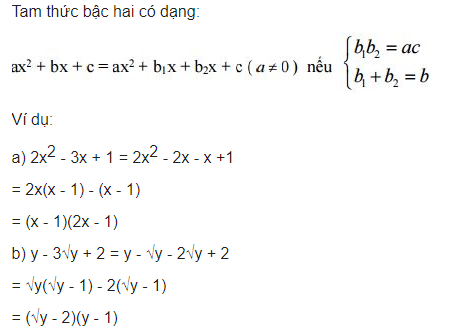
ví dụ 1

Hệ số x ² – 15x + 50

Giải pháp

Tìm hai số có tổng là -15 và tích là 50.

⟹ (-5) + (-10) = -15

⟹ (-5) x (-10) = 50

Viết lại đa thức đã cho thành;

x ² -15x + 50⟹ x ² -5x – 10x + 50

Xác định số liệu từng nhóm;

⟹ x (x – 5) – 10 (x – 5)

⟹ (x – 5) (x – 10)

Ví dụ 2

Nhân tử của tam thức 6y ²  + 11y + 4 bằng cách nhóm.

Giải pháp

6y ²  + 11y + 4 ⟹ 6y ²  + 3y + y + 4

⟹ (6y ²  + 3y ) + (8y + 4)

⟹ 3y (2y + 1) + 4 (2y + 1)

= (2y + 1) (3y + 4)

Ví dụ 3

Thừa số 2x ² – 5x – 12.

Giải pháp

2x ² – 5x – 12

= 2x ² + 3x – 8x – 12

= x (2x + 3) – 4 (2x + 3)

= (2x + 3) (x – 4)

Ví dụ 4

Yếu tố 3Y ²  + 14y + 8

Giải pháp
3Y ²  + 14y + 8 ⟹ 3Y ²  + 12y + 2y + 8

⟹ (3y ²  + 12y) + (2y + 8)

= 3y (y + 4) + 2 (y + 4)
Do đó,

3Y ²  + 14y + 8 = (y + 4) (3Y + 2)

Ví dụ 5

Hệ số 6x ² – 26x + 28

Giải pháp

Nhân hệ số đứng đầu với số hạng cuối cùng.
⟹ 6 * 28 = 168

Tìm hai số có tổng là tích là 168 và tổng là -26
⟹ -14 + -12 = -26 và -14 * -12 = 168

Viết biểu thức bằng cách thay bx vào hai số.
⟹ 6x ² – 26x + 28 = 6x ²  + -14x + -12x + 28
6x ²  + -14x + -12x + 28 = (6x ²  + -14x) + (-12x + 28)

= 2x (3x + -7) + -4 (3x + -7)
Do đó, 6x ² – 26x + 28 = (3x -7) (2x – 4)

Làm thế nào để nhân tử của các nhị thức bằng cách nhóm?

Nhị thức là một biểu thức có hai số hạng kết hợp với nhau bằng dấu cộng hoặc dấu trừ. Để nhân tử một nhị thức, bốn quy tắc sau được áp dụng:

• ab + ac = a (b + c)
• a ²– b ²  = (a – b) (a + b)
• a ³– b ³  = (a – b) (a ²  + ab + b ² )
• a ³+ b ³  = (a + b) (a ²  – ab + b ² )

Ví dụ 6

Hệ số xyz – x ² z

Giải pháp

xyz – x ² z = xz (y – x)

Ví dụ 7

Hệ số 6a ² b + 4bc

Giải pháp

6a ² b + 4bc = 2b (3a ²  + 2c)

Ví dụ 8

Hệ số hoàn toàn: x ⁶ – 64

Giải pháp

x ⁶ – 64 = (x ³ ) ² – 8 ²

= (x ³ + 8) (x ³ – 8) = (x + 2) (x ² – 2x + 4) (x – 2) (x ² + 2x + 4)

Ví dụ 9

Thừa số: x ⁶ – y ⁶ .

Giải pháp

x ⁶ – y ⁶ = (x + y) (x ² – xy + y ² ) (x – y) (x ² + xy + y ² )

Làm thế nào để nhân tử của đa thức bằng cách nhóm?

Như tên cho thấy, bao thanh toán theo nhóm chỉ đơn giản là quá trình nhóm các điều khoản với các nhân tố chung trước khi bao thanh toán.

Để nhân tử một đa thức bằng cách nhóm, đây là các bước:

• Kiểm tra xem các số hạng của đa thức có thừa số chung lớn nhất (GCF) hay không. Nếu vậy, hãy phân tích và nhớ đưa nó vào câu trả lời cuối cùng của bạn.
• Chia đa thức thành bộ hai.
• Tính ra GCF của mỗi tập hợp.
• Cuối cùng xác định xem các biểu thức còn lại có thể được tính thêm nữa hay không.

Xem thêm:

Những cách giải phương trình khối hay nhất cho học sinh

Nhân đa thức như thế nào? Hướng dẫn cách giải vô cùng hiệu quả

Ví dụ 10

Tính thừa số 2ax + ay + 2bx + bằng

Giải pháp

2ax + ay + 2bx + by
= a (2x + y) + b (2x + y)
= (2x + y) (a + b)

Ví dụ 11

Hệ số ax ²  – bx ²  + ay ²  – by ²  + az ²  – bz ²

Giải pháp

ax ²  – bx ²  + ay ²  – by ²  + az ²  – bz ²
= x ² (a – b) + y ² (a – b) + z ² (a – b)
= (a – b) (x ²  + y ²  + z ² )

Ví dụ 12

Hệ số 6x ²  + 3xy – 2ax – ay

Giải pháp

6x ²  + 3xy – 2ax – ay
= 3x (2x + y) – a (2x + y)
= (2x + y) (3x – a)

Ví dụ 13

x ³  + 3x ²  + x + 3

Giải pháp

x ³  + 3x ²  + x + 3
= (x ³  + 3x ² ) + (x + 3)
= x ² (x + 3) + 1 (x + 3)
= (x + 3) (x ²  + 1)

Ví dụ 14

6x + 3xy + y + 2

Giải pháp

6x + 3xy + y + 2

= (6x + 3xy) + (y + 2)

= 3x (2 + y) + 1 (2 + y)

= 3x (y + 2) + 1 (y + 2)

= (y + 2) (3x + 1)

= (3x + 1) (y + 2)

Ví dụ 15

ax ²  – bx ²  + ay ²  – by ²  + az ²  – bz ^{2 Lời}
giải
ax ²  – bx ²  + ay ²  – by ²  + az ²  – bz ²

Suy ra GCF trong mỗi nhóm của hai số hạng ⟹ x ² (a – b) + y ² (a – b) + z ² (a – b)
= (a – b) (x ²  + y ²  + z ² )

Ví dụ 16

Thừa số 6x ²  + 3x + 20x + 10.

Giải pháp

Tính ra GCF trong mỗi nhóm gồm hai thuật ngữ.

⟹ 3x (2x + 1) + 10 (2x + 1)

= (3x + 10) (2x + 1)

Câu hỏi thực hành

Nhân tử bằng cách nhóm các đa thức sau:

1. 15ab ² – 20a ² b
2. 9n – 12n ²
3. 24x ³  – 36x ² y
4. 10x ³ – 15x ²
5. 36x ³ y – 60x ² y ³ z
6. 9x ³  – 6x ²  + 12x
7. 18a ³ b ³ – 27a ² b ³  + 36a ³ b ²
8. 14x ³ + 21x ⁴ y – 28x ² y ²
9. 6ab – b ²  + 12ac – 2bc
10. x ³ – 3x ²  + x – 3
11. ab (x ² + y ² ) – xy (a ²  + b ² )

Câu trả lời

1. 5ab (3b – 4a)
2. 3n (3 – 4n)
3. 12x ² (2x – 3y)
4. 5x ² (2x – 3)
5. 12x ² y (3x – 5y ² z)
6. 3x (3x ² – 2x + 4)
7. 9a ² b ² (2ab – 3b + 4a)
8. 7x ² (2x + 3xy – 4y ² )
9. (b + 2c) (6a – b)
10. (x ² + 1) (x – 3)
11. (bx – ay) (ax – by)