Những cách giải phương trình khối hay nhất cho học sinh

Giải phương trình khối – Phương pháp & Ví dụ

Giải phương trình đa thức bậc cao là một kỹ năng cần thiết cho bất kỳ ai nghiên cứu khoa học và toán học. Tuy nhiên, việc hiểu được cách giải những loại phương trình này khá khó khăn.

Trong bài này, chúng ta sẽ tìm hiểu cách giải phương trình bậc ba bằng các phương pháp khác nhau như phương pháp chia, Định lý nhân tử và phân tích theo nhóm.

Nhưng trước khi đi vào chủ đề này, chúng ta hãy thảo luận về phương trình đa thức và bậc ba là gì.

Đa thức là một biểu thức đại số có một hoặc nhiều số hạng, trong đó hằng số và biến số được phân tách bằng một phép cộng hoặc một dấu trừ.

Dạng tổng quát của đa thức là ax ⁿ  + bx ^n-1  + cx ^n-2  +…. + kx + l, trong đó mỗi biến có một hằng số đi kèm như hệ số của nó. Các loại đa thức khác nhau bao gồm; nhị thức, tam thức và tứ thức. Ví dụ về đa thức là; 3x + 1, x ²  + 5xy – ax – 2ay, 6x ²  + 3x + 2x + 1, v.v.

Phương trình bậc ba là một phương trình đại số bậc ba.
Dạng tổng quát của hàm số bậc ba là: f (x) = ax ³ + bx ² + cx ¹ + d. Và phương trình bậc ba có dạng ax ³ + bx ² + cx + d = 0, trong đó a, b và c là các hệ số và d là hằng số.

Làm thế nào để giải phương trình khối?

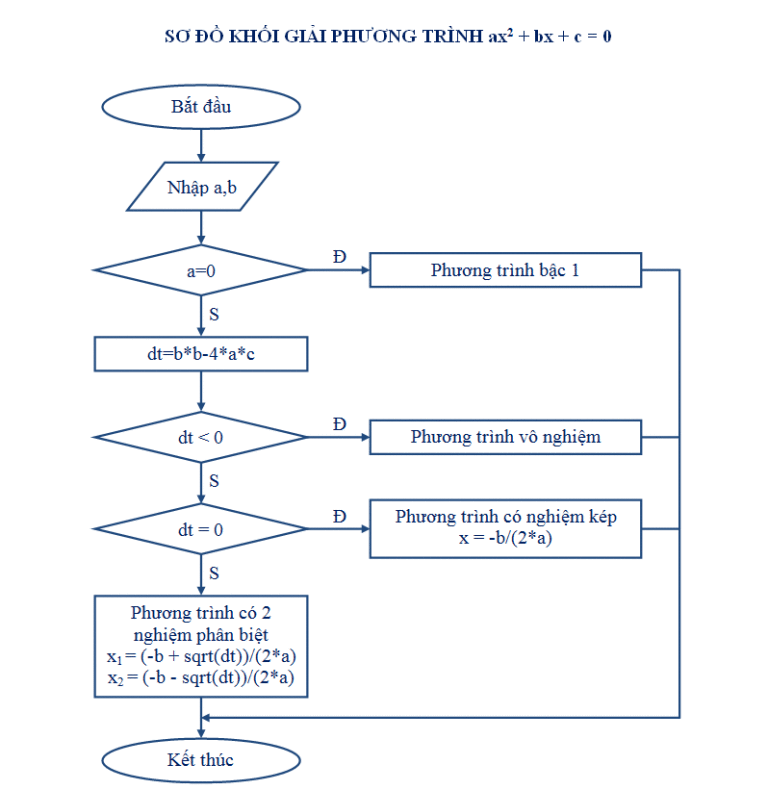
Cách truyền thống để giải một phương trình bậc ba là rút gọn nó thành một phương trình bậc hai và sau đó giải bằng cách tính theo thừa số hoặc công thức bậc hai.

Giống như một phương trình bậc hai có hai nghiệm thực , một phương trình bậc ba có thể có ba nghiệm thực. Nhưng không giống như phương trình bậc hai có thể không có nghiệm thực, phương trình bậc ba có ít nhất một căn thực.

Hai gốc còn lại có thể là thực hoặc tưởng tượng.

Bất cứ khi nào bạn được cung cấp một phương trình bậc ba, hoặc bất kỳ phương trình nào, bạn luôn phải sắp xếp nó ở dạng chuẩn trước.

Ví dụ, nếu bạn được cho một cái gì đó như thế này, 3x ² + x – 3 = 2 / x, bạn sẽ sắp xếp lại thành dạng chuẩn và viết nó như, 3x ³ + x ² – 3x – 2 = 0. Sau đó, bạn có thể giải quyết điều này bằng bất kỳ phương pháp phù hợp nào.

Hãy xem một vài ví dụ dưới đây để hiểu rõ hơn:

ví dụ 1

Xác định nghiệm nguyên của phương trình bậc ba 2x ³  + 3x ²  – 11x – 6 = 0

Giải pháp

Vì d = 6 nên các thừa số khả dĩ là 1, 2, 3 và 6.

Bây giờ hãy áp dụng Định lý Hệ số để kiểm tra các giá trị có thể bằng phép thử và sai.

f (1) = 2 + 3 – 11 – 6 ≠ 0
f (–1) = –2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0

Do đó, x = 2 là căn bậc nhất.

Chúng ta có thể lấy các nghiệm nguyên khác của phương trình bằng phương pháp chia tổng hợp.
= (x – 2) (ax ²  + bx + c)
= (x – 2) (2x ²  + bx + 3)
= (x – 2) (2x ²  + 7x + 3)
= (x – 2) (2x + 1) (x +3)

Do đó, các nghiệm là x = 2, x = -1/2 và x = -3.

Ví dụ 2

Tìm nghiệm nguyên của phương trình bậc ba x ³ – 6x ² + 11x – 6 = 0

Giải pháp

x ³ – 6x ² + 11x – 6

(x – 1) là một trong những hệ số.

Bằng cách chia x ³ – 6x ² + 11x – 6 cho (x – 1),

⟹ (x – 1) (x ² – 5x + 6) = 0

⟹ (x – 1) (x – 2) (x – 3) = 0

Các nghiệm của phương trình bậc ba là x = 1, x = 2 và x = 3.

Ví dụ 3

Giải ra x ³  – 2x ²  – x + 2

Giải pháp

Nhân tử hóa phương trình.

x ³  – 2x ²  – x + 2 = x ² (x – 2) – (x – 2)

= (x ²  – 1) (x – 2)

= (x + 1) (x – 1) (x – 2)

x = 1, -1 và 2.

Ví dụ 4

Giải phương trình bậc ba x ³  – 23x ²  + 142x – 120

Giải pháp

Đầu tiên phân tích nhân tử của đa thức.

x ³  – 23x ²  + 142x – 120 = (x – 1) (x ²  – 22x + 120)

Nhưng x ²  – 22x + 120 = x ²  – 12x – 10x + 120

= x (x – 12) – 10 (x – 12)
= (x – 12) (x – 10)

Do đó, x ³  – 23x ²  + 142x – 120 = (x – 1) (x – 10) (x – 12)

Công bằng mỗi yếu tố bằng không.

x – 1 = 0

x = 1

x – 10 = 10

x – 12 = 0

x = 12

Các nghiệm nguyên của phương trình là x = 1, 10 và 12.

Ví dụ 5

Giải phương trình bậc ba x ³  – 6 x ²  + 11x – 6 = 0.

Giải pháp

Để giải bài toán này bằng phương pháp chia, lấy bất kỳ thừa số nào của hằng số 6;

cho x = 2

Chia đa thức cho x-2 thành

(x ²  – 4x + 3) = 0.

Bây giờ giải phương trình bậc hai (x ²  – 4x + 3) = 0 để có x = 1 hoặc x = 3

Do đó, các nghiệm là x = 2, x = 1 và x = 3.

Ví dụ 6

Giải phương trình bậc ba x ³  – 7x ²  + 4x + 12 = 0

Giải pháp

Cho f (x) = x ³  – 7x ²  + 4x + 12

Vì d = 12 nên các giá trị có thể là 1, 2, 3, 4, 6 và 12.

Bằng phép thử và sai, chúng ta thấy rằng f (–1) = –1 – 7 – 4 + 12 = 0

Vì vậy, (x + 1) là một nhân tử của hàm số.

x ³  – 7x ²  + 4x + 12
= (x + 1) (x ²  – 8x + 12)
= (x + 1) (x – 2) (x – 6)

Do đó x = –1, 2, 6

Ví dụ 7

Giải phương trình bậc ba sau:

x ³  + 3x ²  + x + 3 = 0.

Giải pháp

x ³  + 3x ²  + x + 3
= (x ³  + 3x ² ) + (x + 3)
= x ² (x + 3) + 1 (x + 3)
= (x + 3) (x ²  + 1)

Do đó, x = -1, 1 -3.

Ví dụ 8

Giải ra x ³ – 6x ² + 11x – 6 = 0

Giải pháp

Cơ sở hóa

x ³ – 6x ² + 11x – 6 = 0 ⟹ (x – 1) (x – 2) (x – 3) = 0

Cân bằng mỗi yếu tố với 0 sẽ cho;

x = 1, x = 2 và x = 3

Ví dụ 9

Giải ra x ³ – 4x ² – 9x + 36 = 0

Giải pháp

Nhân số hóa mỗi bộ gồm hai số hạng.

x ² (x – 4) – 9 (x – 4) = 0

Trích nhân tử chung (x – 4) để cho

(x ² – 9) (x – 4) = 0

Bây giờ phân tích sự khác biệt của hai hình vuông

(x + 3) (x – 3) (x – 4) = 0

Bằng cách đánh đồng từng yếu tố với 0, chúng ta nhận được;

x = −3, 3 hoặc 4

Ví dụ 10

Giải phương trình 3x ³  −16x ²  + 23x – 6 = 0

Giải pháp

Chia 3x ³  −16x ²  + 23x – 6 cho x -2 để được 3x ²  – 1x – 9x + 3

= x (3x – 1) – 3 (3x – 1)

= (x – 3) (3x – 1)

Do đó, 3x ³  −16x ²  + 23x – 6 = (x- 2) (x – 3) (3x – 1)

Công bằng mỗi hệ số với 0 để nhận được,

x = 2, 3 và 1/3

Ví dụ 11

Tìm nghiệm nguyên của 3x ³  – 3x ²  – 90x = 0

Giải pháp

nhân nó ra 3x

3x ³  – 3x ²  – 90x ⟹3x (x ²  – x – 30)

Tìm một cặp thừa số có tích là −30 và tổng là −1.

⟹- 6 * 5 = -30

⟹ −6 + 5 = -1

Viết lại phương trình bằng cách thay thế thuật ngữ “bx” bằng các hệ số đã chọn.

⟹ 3x [(x ²  – 6x) + (5x – 30)]

Yếu tố phương trình;

⟹ 3x [(x (x – 6) + 5 (x – 6)]

= 3x (x – 6) (x + 5)

Bằng cách đánh đồng từng yếu tố với 0, chúng ta nhận được;

x = 0, 6, -5

Xem thêm:

Định lý nhị thức dễ hiểu ai cũng học được

Định lý phần dư dễ nhất cho người mới làm quen

Giải phương trình bậc ba bằng phương pháp đồ thị

Nếu bạn không thể giải phương trình bậc ba bằng bất kỳ phương pháp nào ở trên, bạn có thể giải bằng đồ thị. Để làm được điều đó, bạn cần có một bản phác thảo chính xác của phương trình bậc ba đã cho.

(Các) điểm mà đồ thị của nó đi qua trục x, là một nghiệm của phương trình. Số nghiệm thực của phương trình bậc ba bằng số lần đồ thị của nó đi qua trục x.

Ví dụ 12

Tìm nghiệm nguyên của x ³  + 5x ²  + 2x – 8 = 0 bằng đồ thị.

Giải pháp

Chỉ cần vẽ đồ thị của hàm số sau bằng cách thay các giá trị ngẫu nhiên của x:

f (x) = x ³  + 5x ²  + 2x – 8

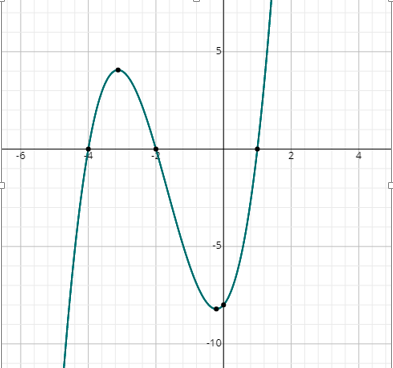
Bạn có thể thấy đồ thị cắt trục x tại 3 điểm, do đó, có 3 nghiệm thực.

Từ biểu đồ, các giải pháp là:

x = 1, x = -2 & x = -4.

Câu hỏi thực hành

Giải các phương trình bậc ba sau:

1. x ³ – 4x ² – 6x + 5 = 0
2. 2x ³ – 3x ² – 4x – 35 = 0
3. x ³ – 3x ² – x + 1 = 0
4. x ³ + 3x ² – 6x – 8 = 0
5. x ³ + 4x ² + 7x + 6 = 0
6. 2x ³ + 9x ² + 3x – 4 = 0
7. x ³ + 9x ² + 26x + 24 = 0
8. x ³ – 6x ² – 6x – 7 = 0
9. x ³ – 7x – 6 = 0
10. x ³ – 5x ² – 2x + 24 = 0
11. 2x ³ + 3x ² + 8x + 12 = 0
12. 5x ³ – 2x ² + 5x – 2 = 0
13. 4x ³ + x ² – 4x – 1 = 0
14. 5x ³ – 2x ² + 5x – 2 = 0
15. 4x ³ – 3x ² + 20x – 15 = 0
16. 3x ³ + 2x ² – 12x – 8 = 0
17. x ³ + 8 = 0
18. 2x ³ – x ² + 2x – 1 = 0
19. 3x ³ – 6x ² + 2x – 4 = 0
20. 3x ³ + 5x ² – 3x – 5 = 0