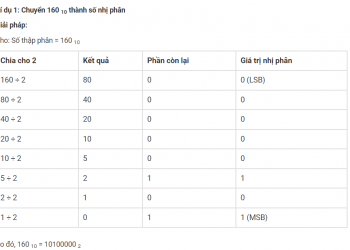
dYdt=dYdx×dxdt
Quy tắc chuỗi này cũng có thể được viết lại thành,
dYdx=dYdtdxdt (Ở đâu dxdt≠ 0 )
Ngoài ra, như đã đề cập trước đó y ‘= g’ (t) = dYdt a n d x′=f′( t ) =dxdt
Vì vậy, chúng ta có thể nói rằng,
dYdx=g′( t )f′( t ) (trong đó f ‘(t) ≠ 0 )
Quy tắc giải các bài toán về đạo hàm của hàm số biểu thị dưới dạng tham số:
Bước i) Trước hết chúng ta viết các hàm x và y đã cho dưới dạng tham số t.
Bước ii) Sử dụng sự khác biệt để tìm ra dYdt a n d dxdt .
Bước iii) Sau đó, sử dụng công thức được sử dụng để giải các hàm ở dạng tham số, tức làdYdx=dYdtdxdt
Bước iv) Cuối cùng thay thế các giá trị của dYdt a n d dxdt và đơn giản hóa để thu được kết quả.
Phương trình tham số là gì?
Khi một nhóm đại lượng của một hoặc nhiều biến độc lập được hình thành dưới dạng hàm, thì chúng được gọi là phương trình tham số. Chúng được sử dụng để biểu diễn tọa độ của một điểm cho bất kỳ đối tượng hình học nào như đường cong, bề mặt, v.v., trong đó phương trình của những đối tượng này được cho là biểu diễn tham số của đối tượng cụ thể đó.
Dạng tổng quát của phương trình tham số là:
x = cos t
y = sin t
Ở đây, (x, y) = (cos t, sin t) tạo thành dạng tham số của đường tròn đơn vị sao cho t là tham số và (x, y ) là các điểm trên đường tròn đơn vị.
Các ứng dụng
Các hàm tham số chủ yếu được sử dụng trong việc tích hợp các loại hàm khác nhau mà hàm đã cho ở dạng phức tạp. Trong những trường hợp như vậy, tham số t được sử dụng để thay thế cho một số phần của hàm đã cho. Các ứng dụng khác bao gồm đồ thị của các hàm và phương trình khác nhau liên quan đến sự phân biệt, v.v.
Bây giờ chúng ta hãy xem qua một số ví dụ để có cái nhìn sâu sắc hơn cho việc giải các hàm của dạng tham số.
Các câu hỏi và giải pháp về phân biệt tham số
Ví dụ 1: Tìm giá trị củadYdx cho các hàm sau được biểu diễn dưới dạng tham số.
i) x = sin t, y = t2
ii) x = 3t3, và= 3t4+ 5
Giải pháp 1:
i) Vì hàm này được biểu diễn ở định dạng hàm tham số nên chúng ta cần tìm ra giá trị dYdt a n ddxdt.
Hiện nay, dYdt= 2 t
dxdt= c o s t
Bây giờ với sự trợ giúp của quy tắc chuỗi, chúng tôi có thể viết,
dYdx=dYdtdxdt
Bây giờ thay thế giá trị của dYdt a n d dxdt vào phương trình trên, chúng ta có thể tìm thấy đạo hàm của wrt x
⇒dYdx=2 tc o s t
Đây là giải pháp bắt buộc của sự phân biệt của phương trình tham số.
ii) Các chức năng này đã được thể hiện dưới dạng t. Do đó, để tìmdYdx , đánh giá dYdt a n d dxdt riêng biệt.
dYdt= 12t3
dxdt=– 9t4
Chúng ta biết rằng,
dYdx=dYdtdxdt
dYdx=12t3– 9t4
dYdx=– 4t73
Đây là giải pháp bắt buộc của sự phân biệt của phương trình tham số.
Ví dụ 2: Tìm giá trị của dYdx cho y = es tôi n t và x = 3t3
Giải pháp 2: Các hàm số đã cho có bản chất là tham số.
Và chúng tôi biết, dYdx=dYdtdxdt
dYdt=es tôi n t× c o s t
dxdt= 9t2
⇒dYdx=es tôi n t× c o s t9t2
Xem thêm bài viết:
Cách để hoàn thành bình phương nhanh nhất hiện nay