Cách để hoàn thành bình phương nhanh nhất hiện nay

Hoàn thành hình vuông – Giải thích & Ví dụ

Cho đến nay, bạn đã học cách tính thừa số các trường hợp đặc biệt của phương trình bậc hai bằng cách sử dụng sự khác biệt của phương pháp tam thức bậc hai bình phương và hoàn hảo.

Các phương pháp này tương đối đơn giản và hiệu quả; tuy nhiên, chúng không phải lúc nào cũng áp dụng được cho tất cả các phương trình bậc hai.

Trong bài này, chúng ta sẽ tìm hiểu cách giải tất cả các dạng phương trình bậc hai bằng một phương pháp đơn giản được gọi là hoàn thành bình phương . Nhưng trước đó, chúng ta hãy tìm hiểu tổng quan về phương trình bậc hai.

Phương trình bậc hai là một đa thức bậc hai thường ở dạng f (x) = ax ²  + bx + c trong đó a, b, c, ∈ R và a ≠ 0. Thuật ngữ ‘a’ được gọi là bậc nhất hệ số, trong khi ‘c’ được gọi là số hạng tuyệt đối của f (x).

Mọi phương trình bậc hai đều có hai giá trị của biến số chưa biết thường được gọi là nghiệm nguyên của phương trình (α, β). Các nghiệm nguyên của phương trình bậc hai có thể thu được bằng cách tính thừa số của phương trình.

Hoàn thành Quảng trường là gì?

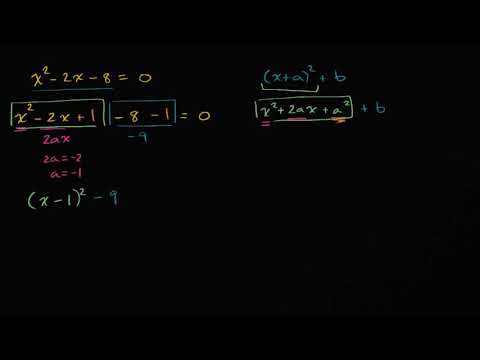
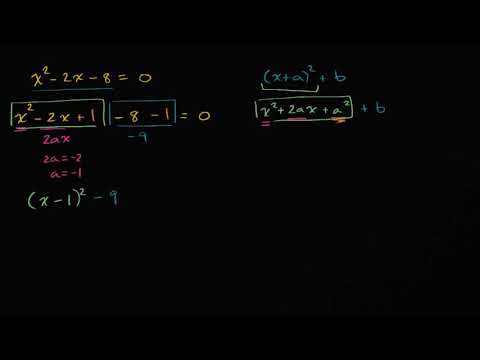
Hoàn thành bình phương là một phương pháp giải phương trình bậc hai không thể phân tích.

Hoàn thành bình phương đơn giản có nghĩa là thao tác với dạng của phương trình để vế trái của phương trình là một tam thức bình phương hoàn hảo.

Làm thế nào để hoàn thành quảng trường?

Để giải một phương trình bậc hai; ax ²  + bx + c = 0 bằng cách hoàn thành hình vuông.

Sau đây là các thủ tục:

• Thao tác với phương trình ở dạng, sao cho chữ c nằm ở vế phải.
• Nếu hệ số đứng đầu a không bằng 1, thì chia mỗi số hạng của phương trình cho a, sao cho hệ số của x ² là 1.
• Cộng cả hai vế của phương trình với bình phương của một nửa đồng hiệu của số hạng-x

⟹ (b / 2a) ² .

• Thừa số vế trái của phương trình là bình phương của nhị thức.
• Tìm căn bậc hai của cả hai vế của phương trình. Áp dụng quy tắc (x + q) ²= r, trong đó

x + q = ± √r

• Giải cho biến x

Hoàn thành công thức bình phương

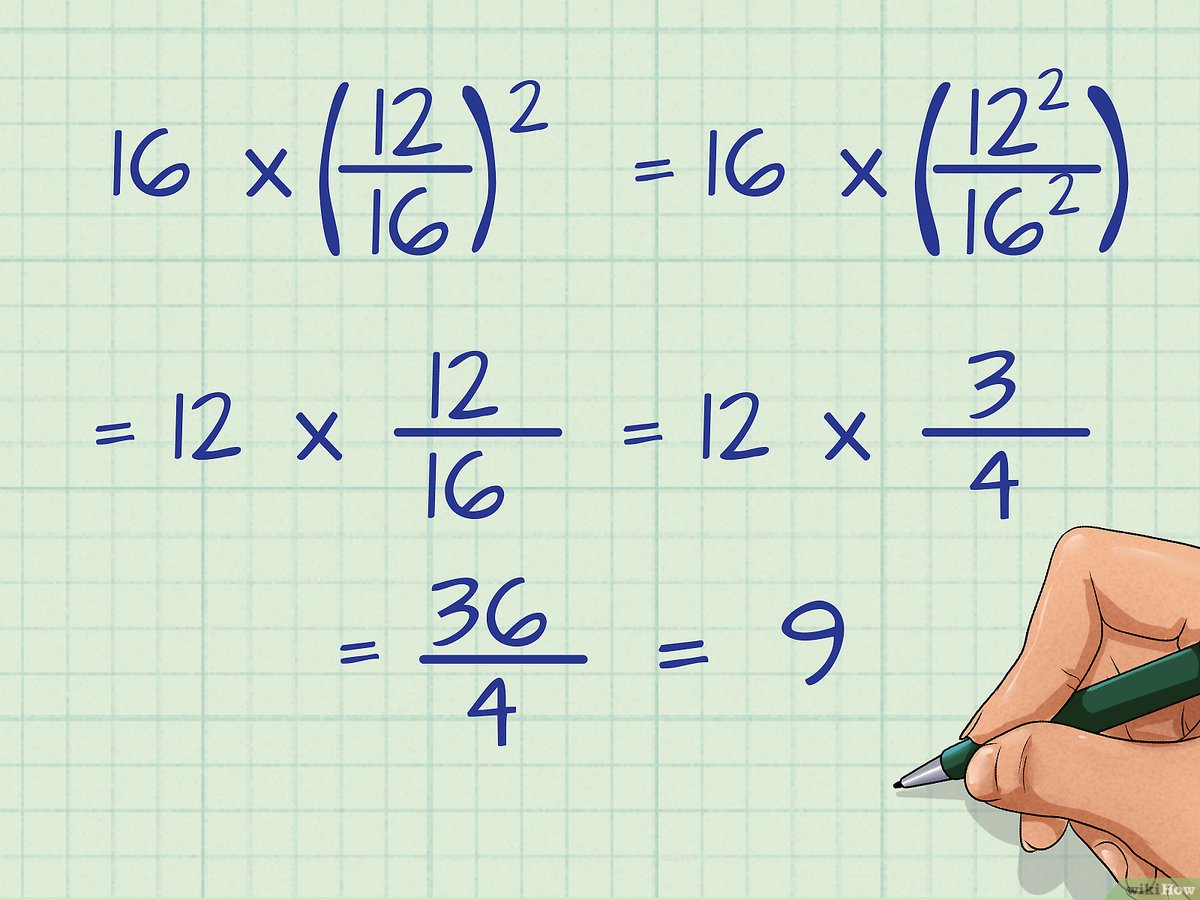
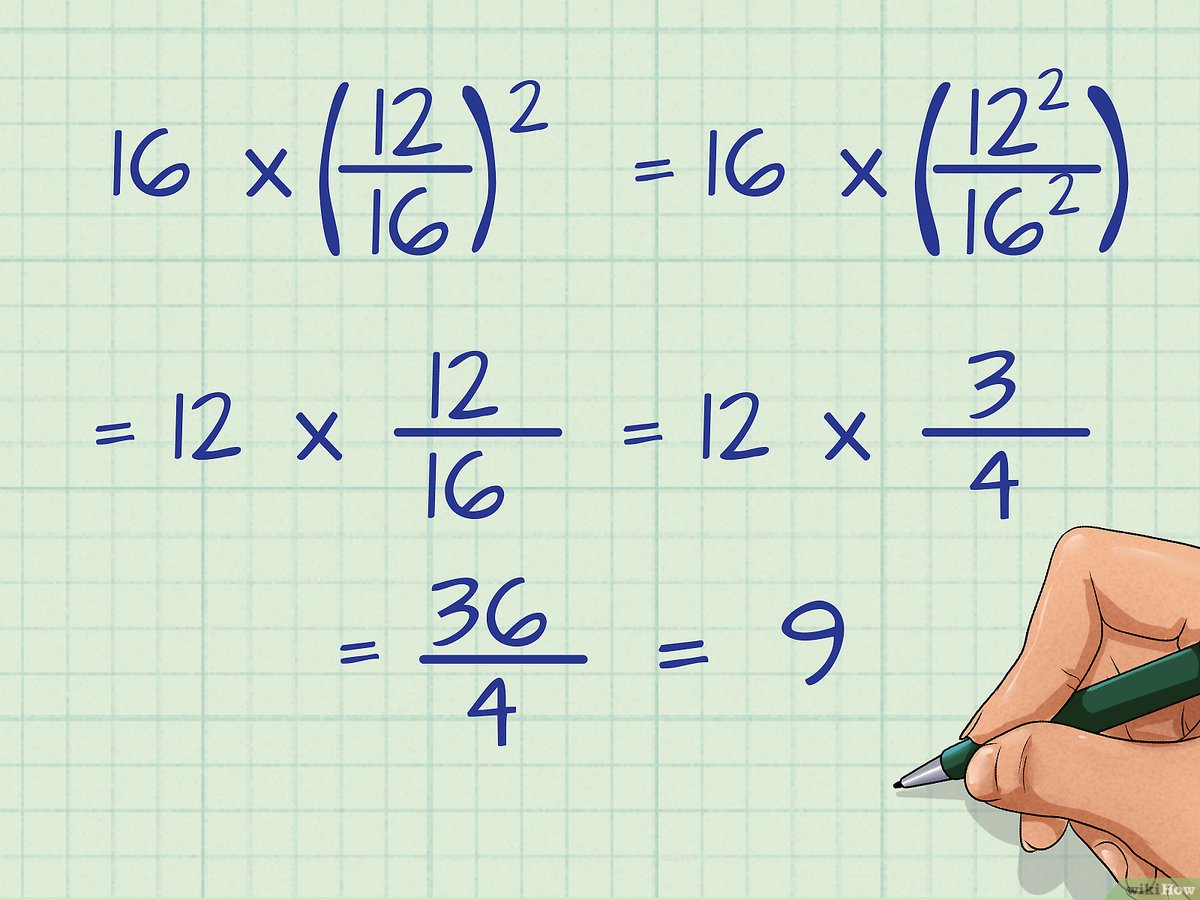
Trong toán học, hoàn thành bình phương được sử dụng để tính đa thức bậc hai. Hoàn thành Công thức Bình phương đã cho là: ax ² + bx + c ⇒ (x + p) ² + hằng số.

Công thức bậc hai được suy ra bằng phương pháp hoàn thành bình phương. Hãy xem nào.

Cho phương trình bậc hai ax ² + bx + c = 0;

Cô lập số hạng c sang vế phải của phương trình

ax ² + bx = -c

Chia mỗi số hạng cho a.

x ² + bx / a = -c / a

Viết dưới dạng một hình vuông hoàn hảo
x ² + b x / a + (b / 2a) ² = – c / a + (b / 2a) ²

(x + b / 2a) ² = (-4ac + b ² ) / 4a ²

(x + b / 2a) = ± √ (-4ac + b ² ) / 2a

x = – b / 2a ± √ (b ² – 4ac) / 2a

x = [- b ± √ (b ² – 4ac)] / 2a ………. (Đây là công thức bậc hai)

Bây giờ chúng ta hãy giải một vài phương trình bậc hai bằng cách sử dụng phương pháp bình phương hoàn thành.

ví dụ 1

Giải phương trình bậc bốn sau đây bằng cách hoàn thành phương pháp bình phương:

x ²  + 6x – 2 = 0

Giải pháp

Biến đổi phương trình x ²  + 6x – 2 = 0 thành (x + 3) ²  – 11 = 0

Vì (x + 3) ²  = 11

x + 3 = + √11 hoặc x + 3 = -√11

x = -3 + √11

HOẶC LÀ

x = -3 -√11

Nhưng √11 = 3,317

Do đó, x = -3 +3.317 hoặc x = -3 -3.317,

x = 0,317 hoặc x = -6,317

Ví dụ 2

Giải bằng cách hoàn thành hình vuông x ²  + 4x – 5 = 0

Giải pháp

Hình thức tiêu chuẩn của hình vuông hoàn thành là;
(x + b / 2) ²  = – (c – b ^2/4 )

Trong trường hợp này, b = 4, c = -5. Thay thế các giá trị;
Vậy, (x + 4/2) ²  = – (- 5 – 4 ^2/4 )
(x + 2) ²  = 5 + 4
⇒ (x + 2) ²  = 9
⇒ (x + 2) = ± √9
⇒ (x + 2) = ± 3
⇒ x + 2 = 3, x + 2 = -3
⇒ x = 1, -5

Ví dụ 3

Giải ra x ²  + 10x – 4 = 0

Giải pháp

Viết lại phương trình bậc hai bằng cách cô lập c ở vế phải.

x ²  + 10x = 4

Cộng cả hai vế của phương trình với (10/2) ² = 5 ² = 25.

= x ² + 10x + 25 = 4 + 25

= x ² + 10x + 25 = 29

Viết cạnh trái dưới dạng hình vuông

(x + 5) ² = 29

x = -5 ± √29

x = 0,3852, – 10,3852

Ví dụ 4

Giải hệ 3x ²  – 5x + 2 = 0

Giải pháp

Chia mỗi số hạng của phương trình cho 3 để hệ số đứng đầu bằng 1.
x ²  – 5/3 x + 2/3 = 0
Đối chiếu với dạng chuẩn; (x + b / 2) ²  = – (cb ^2/4 )
b = -5/3; c = 2/3
c – b2 / 4 = 2/3 – [(5/3) 2/4] = 2/3 – 25/36 = -1/36
Do đó,
⇒ (x – 5/6) ²  = 1/36
⇒ (x – 5/6) = ± √ (1/36)
⇒ x – 5/6 = ± 1/6
⇒ x = 1, -2/3

Ví dụ 5

Giải ra x ² – 6x – 3 = 0

Giải pháp

x ² – 6x = 3
x ² – 6x + (-3) ² = 3 + 9

(x – 3) ² = 12

x – 3 = ± √12

x = 3 ± 2√3

Ví dụ 6

Giải: 7x ² – 8x + 3 = 0

Giải pháp

7x ² – 8x = −3

x ² −8x / 7 = −3/7

x ² – 8x / 7 + (- 4/7) ² = −3/7 + 16/49

(x – 4/7) ² = −5/49

x = 4/7 ± (√7) i / 5

(x – 3) ² = 12

x – 3 = ± √12

x = 3 ± 2√3

Ví dụ 7

Giải 2x ²  – 5x + 2 = 0

Giải pháp

Chia mỗi số hạng cho 2

x ²  – 5x / 2 + 1 = 0

⇒ x ²  – 5x / 2 = -1

Thêm (1/2 × −5/2) = 25/16 vào cả hai vế của phương trình.

= x ²  – 5x / 2 + 25/16 = -1 + 25/16

= (x – 5/4) ²  = 9/16

= (x – 5/4) ²  = (3/4) ²

⇒ x – 5/4 = ± 3/4

⇒ x = 5/4 ± 3/4

x = 1/2, 2

Ví dụ 8

Giải ra x ² – 10x -11 = 0

Giải pháp

Viết tam thức dưới dạng bình phương hoàn hảo
(x ² – 10x + 25) – 25 – 11 = 36

⇒ (x – 5) ² – 36 = 0

⇒ (x – 5) ² = 36

Tìm các căn bậc hai trên cả hai vế của phương trình

x – 5 = ± √36

x -5 = ± 6

x = −1 hoặc x = 11

Ví dụ 9

Giải phương trình sau bằng cách điền vào ô vuông

x ² + 10x – 2 = 0

Giải pháp

x ² + 10x – 2 = 0

⇒ x ² + 10x = 2

⇒ x ² + 10x + 25 = 2 + 25

⇒ (x + 5) ² = 27

Tìm các căn bậc hai trên cả hai vế của phương trình

⇒ x + 5 = ± √27

⇒ x + 5 = ± 3√3

x = -5 ± 3√3

Ví dụ 10

Giải ra x ² + 4x + 3 = 0

Giải pháp

x ² + 4x + 3 = 0 ⇒ x ² + 4x = -3

x ² + 4x + 4 = – 3 + 4

Viết tam thức dưới dạng một hình vuông hoàn hảo

(x + 2) ² = 1

Xác định căn bậc hai của cả hai vế.

(x + 2) = ± √1

x = -2 + 1 = -1

HOẶC LÀ

x = -2-1 = -3

Ví dụ 11

Giải phương trình dưới đây bằng phương pháp hoàn thành bình phương.

2x ²  – 5x + 1 = 0

Giải pháp

x ² −5 x / 2 + 1/2 = 0

x ² −5 x / 2 = −1/2

(1/2) (−5/2) = −5 / 4

(−5/4) ² = 25/16

x ² – 5 x / 2 + 25/16 = −1 / 2 + 25/16

(x – 5/4) ² = 17/16

Tìm bình phương của cả hai cạnh.

(x – 5/4) = ± √ (17/16)

x = [5 ± √ (17)] / 4

Xem thêm:

Làm thế nào để nhân chéo hiệu quả nhất

Cách giải công thức bậc hai nhanh gọn dễ hiểu nhất

Câu hỏi thực hành

Giải các phương trình dưới đây bằng phương pháp hoàn thành bình phương.

1. ? ² + 6? + 5 = 0
2. x ² + 8? – 9 = 0
3. x ² – 6? + 9 = 0
4. ? ² + 4? – 7 = 0
5. ? ² – 5? – 24 = 0
6. x ² – 8? + 15 = 0
7. 4x ² – 4? + 17 = 0
8. 9? ² – 12? + 13 = 0
9. 4? ² – 4? + 5 = 0
10. 4? ² – 8? + 1 = 0
11. x ² + 4x – 12 = 0
12. 10x ² + 7x – 12 = 0
13. 10 + 6x – x ² = 0
14. 2x ² + 8x – 25 = 0
15. x ² + 5x – 6 = 0
16. 3x ² – 27x + 9
17. 15 – 10x – x ²
18. 5x ² + 10x + 15
19. 24 + 12x – 2x ²
20. 5x ² + 10x + 15