Khuôn mặt của Hình dạng 3D
- Mặt phẳng của hình đa diện là mặt của nó. Hình dạng rắn có thể có nhiều hơn một mặt. Hình lập phương dưới đây có 6 mặt viz. ABCD, EFGH, ADHE, DHGC, BFGC và AEFB.
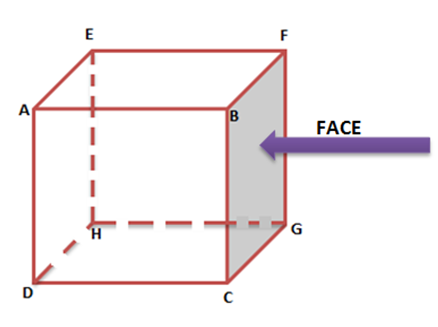

- Hình lập phương và hình lập phương đều có 6 mặt.
- Hình nón có một mặt phẳng và một mặt cong.
- Hình trụ có 2 mặt phẳng và một mặt cong.
- Một hình cầu có một mặt cong.
Các cạnh của Hình dạng 3D
- Các mặt gặp nhau ở các cạnh. Các cạnh là các đường thẳng đóng vai trò là đường giao nhau của hai mặt. Hình lập phương dưới đây có 12 cạnh là AB, BF, EF, AE, AD, DH, EH, HG, FG, BC, CG và CD.
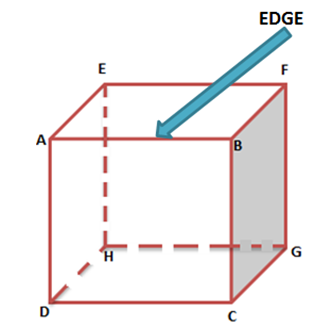

- Hình lập phương và hình lập phương đều có 12 cạnh.
- Hình nón có 1 cạnh.
- Hình trụ có 2 cạnh.
- Một hình cầu không có cạnh.
Dọc của Hình dạng 3D
- Các giao điểm của các cạnh biểu thị các đỉnh. Các đỉnh được biểu diễn bằng các điểm. Trong hình lập phương bên dưới, A, B, C, D, E, F, G và H là 8 đỉnh của hình lập phương.
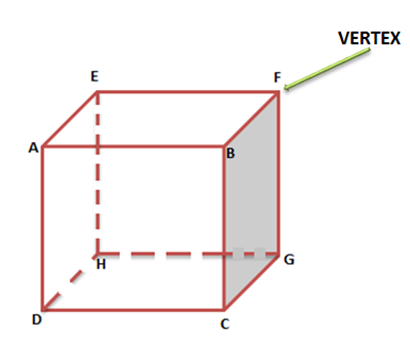

- Hình lập phương và hình lập phương đều có 8 đỉnh.
- Hình nón có 1 đỉnh.
- Hình trụ không có đỉnh.
- Hình cầu không có đỉnh (bề mặt là một đường cong).
Bây giờ, chúng ta đã quen thuộc với các khối đa diện, hãy chuyển sang các loại của chúng.
Các loại đa diện
- Khối đa diện lồi: Nếu bề mặt của một khối đa diện (bao gồm các mặt, các cạnh và các đỉnh của nó) không tự cắt nhau và đoạn thẳng nối hai điểm bất kỳ của khối đa diện nằm trong phần bên trong hoặc bề mặt của nó thì khối đa diện đó là một khối lồi. hình đa diện.
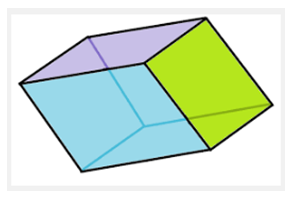

- Khối đa diện lõm: Khối đa diện không lồi được gọi là khối đa diện lõm.


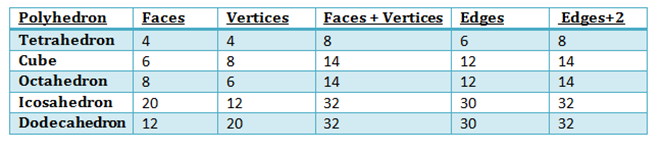
Công thức của Euler :
Theo công thức của Euler cho bất kỳ hình đa diện lồi nào, số Mặt (F) và đỉnh (V) cộng lại với nhau nhiều hơn số cạnh (E) đúng hai lần.
F + V = 2 + E

Một khối đa diện được gọi là khối đa diện đều nếu tất cả các mặt của nó tạo thành các đa giác đều và tại mỗi đỉnh có cùng một số mặt cắt nhau.
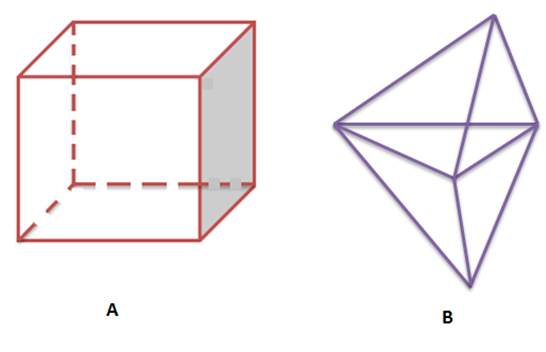

Hình A là một đa diện đều vì tất cả các mặt đều là đa giác đều và B là một đa giác không đều.