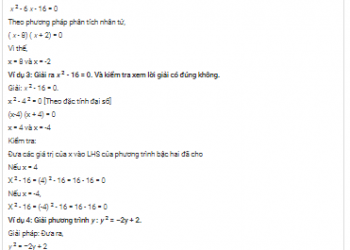• tích vô hướng của vectơ hoặc tích chấm
• tích vectơ của vectơ hoặc tích chéo

Sự khác biệt giữa cả hai phương pháp chỉ là, sử dụng phương pháp đầu tiên, chúng ta nhận được một giá trị vô hướng là kết quả và sử dụng kỹ thuật thứ hai, giá trị thu được lại là một vectơ trong tự nhiên.

Sản phẩm chấm của Vectơ:

Tích vô hướng của hai vectơ a và b có độ lớn | a | và | b | được cho dưới dạng | a || b | cos θ, trong đó θ đại diện cho góc giữa các vectơ a và b lấy theo hướng của các vectơ.
Chúng ta có thể biểu thị tích vô hướng như sau:

ab = | a || b | cosθ

ở đâu | a | và | b | đại diện cho độ lớn của vectơ a và b  trong khi  cos θ biểu thị cosin của góc giữa cả hai vectơ và ab biểu thị tích chấm của hai vectơ.

Trong trường hợp bất kỳ vectơ nào bằng 0, góc θ không được xác định và trong trường hợp như vậy, ab được cho bằng 0.

Phép chiếu Vectơ:

BP đã biết là hình chiếu của vectơ a lên vectơ b theo phương của vectơ b cho bởi | a | cos θ.

Tương tự, hình chiếu của vectơ b lên vectơ a theo phương của vectơ a được cho bởi | b | cos θ.

Phép chiếu của vectơ a theo hướng của vectơ b được biểu thị dưới dạng

B P=a . b| b |

⇒B P-→-=a . b| b |×b^

⇒B P-→- =a . b| b |.b| b |

⇒B P-→- =a . b| b|2b

Tương tự, hình chiếu của vectơ b theo hướng của vectơ a được biểu diễn dưới dạng

B Q = a . b| a |

⇒B Q-→- = a . b| a |×a^

⇒B Q-→- = a . b| a |a| a |

⇒B Q-→- = a . b| a|2a

Như vậy, chúng ta thấy rằng tích chấm của hai vectơ là tích độ lớn của một vectơ với thành phần phân giải của vectơ kia theo hướng của vectơ thứ nhất.

Thuộc tính sản phẩm chấm của Vector:

• Tính chất 1:  Tích của hai vectơ có tính chất giao hoán tức là ab = ba  = ab cos θ.
• Tính chất 2: Nếu ab = 0 thì có thể thấy rõ  b hoặc a bằng 0 hoặc cos θ = 0 ⇒ θ = Số Pi2. Nó gợi ý rằng một trong hai vectơ bằng 0 hoặc chúng vuông góc với nhau.
• Tính chất 3: Chúng ta cũng biết rằng sử dụng tích vô hướng của vectơ (p a ). (Q b ) = (p b ). (Q a ) = pq  ab
• Tính chất 4: Tích số chấm của một vectơ đối với chính nó là bình phương độ lớn của vectơ ieaa = aa cos 0 = a ²
• Tính chất 5: Tích số chấm tuân theo luật phân phối tức là a. (B + c) = ab + ac
• Tính chất 6:  Trong điều kiện tọa độ trực giao của các vectơ vuông góc với nhau, người ta thấy rằngTôi^.Tôi^ = j^.j^= k^.k^ =1
• Tính chất 7:  Xét về vectơ đơn vị nếua= a1Tôi^+a2j^+a3k^ và b =b1Tôi^+b2j^+b3k^sau đó

a . b=(a1Tôi^+a2j^+a3k^) . (b1Tôi^+b2j^+b3k^)

⇒a1b1+a2b2+a3b3 = a b c o s θ

Cũng kiểm tra:  Sản phẩm vectơ

Câu hỏi ví dụ về tích chấm của hai vectơ

Ví dụ 1: Cho có hai vectơ [6, 2, -1] và [5, -8, 2]. Tìm tích số chấm của các vectơ.

Giải pháp:

Cho các vectơ: [6, 2, -1] và [5, -8, 2] lần lượt là a và b.

ab = (6) (5) + (2) (- 8) + (-1) (2)

ab = 30 – 16 – 2

ab = 12

Ví dụ 2: Cho có hai vectơ | a | = 4 và | b | = 2 và θ = 60 °. Tìm sản phẩm chấm của họ.

Giải pháp:

ab = | a || b | cos θ

ab = 4,2 cos 60 °

ab = 4,2 × (1/2)

ab = 4