Giải thích cho cặp góc tuyến tính
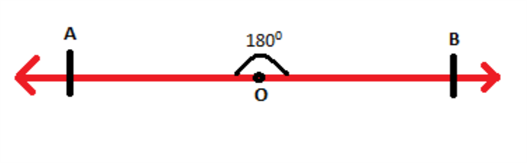
Khi góc giữa hai đường thẳng là 180 °, chúng tạo thành một góc thẳng . Góc thẳng chỉ là một cách khác để biểu diễn một đường thẳng. Một đường thẳng có thể được hình dung như một đường tròn có bán kính vô hạn. Đoạn thẳng là bất kỳ phần nào của dòng có hai điểm cuối. Ngoài ra, một phần của bất kỳ đoạn thẳng nào chỉ có một điểm cuối được gọi là tia. Một đoạn thẳng với A và B là hai điểm cuối được biểu diễn dưới dạngA B¯¯¯¯¯¯¯¯. Hình bên dưới thể hiện đoạn thẳng AB và hai mũi tên ở cuối biểu thị một đoạn thẳng.


Nếu lấy điểm O ở bất kỳ vị trí nào trên đoạn thẳng AB như hình vẽ thì góc giữa hai đoạn thẳng AO và OB là một góc thẳng 180 °.

Hãy xem xét một tia O P-→- đứng trên đoạn thẳng A B¯¯¯¯¯¯¯¯ như hình:
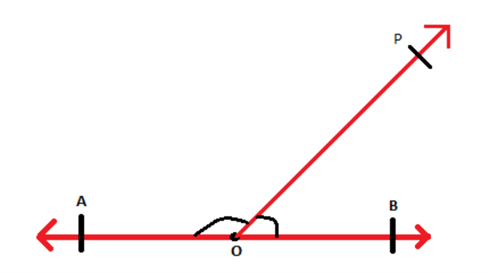

Các góc tạo thành tại O là ∠ POB và ∠ POA . Biết rằng góc giữa hai đoạn thẳng AO và OB là 180 °. do đó, các góc ∠ POB và ∠ POA cộng lại bằng 180 °.
Do đó, ∠ POB + ∠ POA = ∠ AOB = 180 °
∠POB và ∠POA kề nhau và khi tổng các góc kề bằng 180 ° thì các góc đó tạo thành cặp góc tuyến tính.
Thảo luận trên có thể được phát biểu như một tiên đề.
Tiên đề
Tiên đề 1: Nếu một tia đứng trên một đường thẳng thì các góc kề nhau tạo thành một cặp góc thẳng.


Trong hình trên, tất cả các đoạn thẳng đều đi qua điểm O như hình vẽ bên. Khi tia OA nằm trên đoạn thẳng CD, các góc ∠ AOD và ∠ AOC tạo thành một cặp pháp tuyến. Tương tự, ∠ QOD và ∠ POD tạo thành một cặp tuyến tính, v.v.
Điều ngược lại của tiên đề đã nêu cũng đúng, điều này cũng có thể được phát biểu như tiên đề sau.
Tiên đề 2: Nếu hai góc tạo thành một cặp đường thẳng thì nhánh bất thường của cả hai góc tạo thành một đường thẳng.


Hình 3 Các góc liền kề với các thước đo khác nhau
Trong hình minh họa ở trên, chỉ có hình cuối cùng đại diện cho một cặp tuyến tính, vì tổng các góc liền kề là 180 °. Do đó, AB biểu diễn một đoạn thẳng. Hai cặp góc còn lại kề nhau nhưng chúng không tạo thành một cặp góc thẳng. Chúng không tạo thành một đường thẳng.
Hai tiên đề nêu trên tạo thành Tiên đề Cặp tuyến tính và rất hữu ích trong việc giải các bài toán khác nhau.
Thí dụ
Giả sử hai góc ∠AOC và ∠ BOC tạo thành một cặp pháp tuyến tại điểm O thuộc đoạn thẳng AB. Nếu hiệu giữa hai góc là 60 °. Sau đó tìm cả hai góc.
Giải: Cho trước, ∠AOC và ∠ BOC tạo thành một cặp tuyến tính
Vì vậy, ∠AOC + ∠ BOC = 180 ° ……… (1)
Cũng được đưa ra,
∠AOC – ∠ BOC = 60 ° ……… (2)
Thêm eq. 1 và 2, chúng tôi nhận được;
2∠AOC = 180 ° + 60 ° = 240 °
∠AOC = 240 ° / 2 = 120 °
Bây giờ đặt giá trị của ∠AOC trong phương trình 1, chúng ta nhận được;
∠BOC = 180 ° – ∠AOC = 180 ° – 120 °
∠BOC = 60 °
Xem thêm: