• Định nghĩa
• Bằng chứng
• Thuộc tính phản xạ
• Thuộc tính đối xứng
• Thuộc tính bắc cầu
• Các ví dụ
• Vấn đề thực hành

Định nghĩa quan hệ tương đương

Quan hệ R trên tập A được cho là quan hệ tương đương nếu và chỉ khi quan hệ R là phản xạ, đối xứng và bắc cầu.

Phản xạ : Một quan hệ được cho là phản xạ, nếu (a, a) ∈ R, với mọi a ∈ A.

Đối xứng : Một quan hệ được cho là đối xứng, nếu (a, b) ∈ R, thì (b, a) ∈ R.

Transitive : Một quan hệ được cho là bắc cầu nếu (a, b) ∈ R và (b, c) ∈ R, thì (a, c) ∈ R.

Các quan hệ tương đương có thể được giải thích theo các ví dụ sau:

• Dấu của ‘bằng (=)’ trên một tập hợp các số; ví dụ, 1/3 = 3/9.
• Đối với một tập hợp các tam giác đã cho, quan hệ ‘tương tự với (~)’ và ‘đồng dư với (≅)’ cho thấy sự tương đương.
• Đối với một tập hợp các số nguyên đã cho, quan hệ ‘môđun đồng dư n (≡)’ cho thấy sự tương đương.
• Hình ảnh và miền giống nhau dưới một hàm, cho thấy mối quan hệ tương đương.
• Đối với tập hợp tất cả các góc, ‘có cùng cosin’.
• Đối với tập hợp tất cả các số thực, ‘có cùng giá trị tuyệt đối’.

Bằng chứng quan hệ tương đương

Đây là một ví dụ về quan hệ tương đương để chứng minh các thuộc tính.

Giả sử R là một quan hệ trên tập các cặp số nguyên dương có thứ tự sao cho ((a, b), (c, d)) ∈ R nếu và chỉ khi ad = bc. R có phải là quan hệ tương đương không?

Để chứng minh R là một quan hệ tương đương, chúng ta phải chứng minh rằng R là phản xạ, đối xứng và bắc cầu.

Bằng chứng cho điều kiện đã cho được đưa ra dưới đây:

Thuộc tính phản xạ

Theo tính chất phản xạ, nếu (a, a) ∈ R, với mọi a∈A

Đối với tất cả các cặp số nguyên dương,

((a, b), (a, b))) ∈ R.

Rõ ràng, chúng ta có thể nói

ab = ab với mọi số nguyên dương.

Do đó, tính chất phản xạ được chứng minh.

Thuộc tính đối xứng

Từ tính chất đối xứng,

nếu (a, b) ∈ R, thì chúng ta có thể nói (b, a) ∈ R

Đối với điều kiện đã cho,

nếu ((a, b), (c, d))) ∈ R, thì ((c, d), (a, b)) ∈ R.

Nếu ((a, b), (c, d)) ∈ R, thì ad = bc và cb = da

vì phép nhân có tính chất giao hoán.

Do đó ((c, d), (a, b)) ∈ R

Do đó tính chất đối xứng được chứng minh.

Thuộc tính bắc cầu

Từ thuộc tính bắc cầu,

nếu (a, b) ∈ R và (b, c) ∈ R, thì (a, c) cũng thuộc R

Đối với tập hợp các cặp số nguyên dương có thứ tự đã cho,

((a, b), (c, d)) ∈ R và ((c, d), (e, f)) ∈ R,

thì ((a, b), (e, f) ∈ R.

Bây giờ, giả sử rằng ((a, b), (c, d))) ∈ R và ((c, d), (e, f)) ∈ R.

Sau đó, chúng tôi nhận được, ad = cb và cf = de.

Quan hệ trên ngụ ý rằng a / b = c / d và c / d = e / f,

nên a / b = e / f ta được af = be.

Do đó ((a, b), (e, f))) ∈ R.

Do đó tính chất bắc cầu được chứng minh.

Ví dụ về quan hệ tương đương

Xem qua các ví dụ và giải pháp quan hệ tương đương được cung cấp tại đây

Câu hỏi 1:

Giả sử rằng F là một quan hệ trên tập R các số thực được xác định bởi xFy nếu và chỉ khi xy là một số nguyên. Chứng minh rằng F là một quan hệ tương đương trên R.

Giải pháp:

Suy ra: Xét x thuộc R thì x – x = 0 là số nguyên. Do đó xFx.

Tính đối xứng: Xét x và y thuộc R và xFy. Khi đó x – y là một số nguyên. Như vậy, y – x = – (x – y), y – x cũng là một số nguyên. Do đó yFx.

Phép bắc cầu : Xét x và y thuộc R , xFy và yFz. Do đó xy và yz là các số nguyên. Theo tính chất bắc cầu, (x – y) + (y – z) = x – z cũng là một số nguyên. Vì vậy, xFz đó.

Do đó, R là một quan hệ tương đương trên R .

Câu hỏi 2:

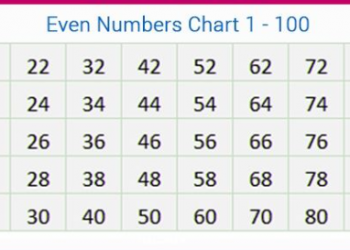
Chứng tỏ rằng quan hệ R là quan hệ tương đương trong tập A = {1, 2, 3, 4, 5} cho bởi quan hệ R = {(a, b): | ab | là thậm chí}.

Solutio:

R = {(a, b): | ab | là thậm chí}. Trong đó a, b thuộc A

Thuộc tính phản xạ:

Từ quan hệ đã cho,

| a – a | = | 0 | = 0

Và 0 luôn luôn là số chẵn.

Do đó, | aa | là thậm chí

Do đó, (a, a) thuộc R

Do đó R là phản xạ

Thuộc tính đối xứng:

Từ quan hệ đã cho,

| a – b | = | b – a |

Chúng ta biết rằng | a – b | = | – (b – a) | = | b – a |

Do đó | a – b | là thậm chí,

Khi đó | b – a | cũng là thậm chí.

Do đó, nếu (a, b) ∈ R thì (b, a) thuộc R

Do đó R là đối xứng.

Thuộc tính bắc cầu:

Nếu | ab | là chẵn, thì (ab) là chẵn.

Tương tự, nếu | bc | là chẵn, sau đó (bc) cũng là chẵn.

Tổng của số chẵn cũng là số chẵn

Vì vậy, chúng ta có thể viết nó là a-b + bc là số chẵn

Sau đó, a – c cũng chẵn

Vì thế,

| a – b | và | b – c | chẵn thì | ac | là thậm chí.

Do đó, nếu (a, b) ∈ R và (b, c) ∈ R, thì (a, c) cũng thuộc R

Do đó R có tính bắc cầu.

Thực hành các bài toán về quan hệ tương đương

Giải các bài tập về quan hệ tương đương dưới đây:

1. Chứng minh rằng quan hệ R là quan hệ tương đương, cho rằng tập hợp các số phức được xác định bởi z ₁ R z ₂ ⇔ [(z ₁ -z ₂ ) / (z ₁ + z ₂ )] là thực.
2. Chứng tỏ rằng quan hệ đã cho R là quan hệ tương đương, được xác định bởi (p, q) R (r, s) ⇒ (p + s) = (q + r)
3. Kiểm tra tính chất phản xạ, đối xứng và bắc cầu của quan hệ x R y, nếu và chỉ khi y chia hết cho x, trong đó x, y ∈ N.