Các công thức dạng phép biến hình

Dưới đây là một số công thực có dạng phép biến hình mà tintuctuyensinh đã tổng hợp trong bài viết

công thức dạng phép biến hình

1. Phép biến hình

– Điểm M′M′ gọi là ảnh của điểm MM qua phép biến hình FF , hay MM là điểm tạo ảnh của điểm M′M′, kí hiệu M′=f(M)M′=f(M)

– Nếu (H)(H) là một hình nào đó thì (H′)(H′) gồm các điểm M′M′ là ảnh của M∈HM∈H được gọi là ảnh của (H)(H) qua phép biến hình FF .

– Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép tương đồng.

2. Phép tịnh tiến

a. khái niệm

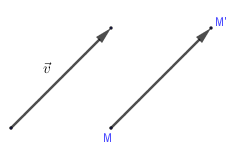
T→v(M)=M′⇔−−−→MM′=→vTv→(M)=M′⇔MM′→=v→

b. thuộc tính

– Nếu phép tịnh tiến biến nhị điểm M,NM,N thành nhị điểm M′,N′M′,N′ thì −−−−→M′N′=−−−→MNM′N′→=MN→ , từ đó suy ra M′N′=MNM′N′=MN

– Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm đổi mới thứ tự ba điểm đó.

– Phép tịnh tiến biến đường thẳng thành đường thẳng đồng thời hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến một tam giác thành một tam giác bằng nó, đường tròn thành đường tròn có cùng bán kính.

c. Biểu thức tọa độ

Trong mặt phẳng tọa độ (Oxy)(Oxy) cho vectơ →v=(a;b),M(x;y)v→=(a;b),M(x;y).

Khi đó phép tịnh tiến theo vectơ →v:T→v(M)=M′(x′;y′)v→:Tv→(M)=M′(x′;y′) có biểu thức tọa độ: {x′=x+ay′=y+b{x′=x+ay′=y+b

3. Phép đối xứng trục

a. Định nghĩa

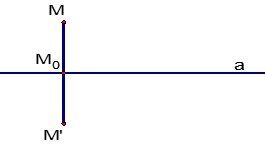
Phép đối xứng qua một đường thẳng aa là phép biến hình biến điểm MM thành điểm M′M′ đối xứng với MM qua đường thẳng aa. Kí hiệu : DaDa (aalà trục đối xứng)

b. tính chất

+) Da(M)=M′⇔−−−−→M0M′=−−−−→M0MDa(M)=M′⇔M0M′→=−M0M→ với M0M0 là hình chiếu của MM trên aa.

+) Da(M)=M⇔M∈aDa(M)=M⇔M∈a

+) Da(M)=M′⇔Da(M′)=MDa(M)=M′⇔Da(M′)=M, aa là trung trực của đoạn MM′MM′.

– Phép đối xứng trục bảo toàn khoảng cách giữa {hai|nhì|nhị} điểm {bất cứ|bất kỳ}.

– Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

– Phép đối xứng trục biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm {đổi mới|thay đổi} {thứ tự|trật tự} ba điểm đó.

c. Biểu thức tọa độ

Trong mặt phẳng tọa độ OxyOxy: Da:M(x;y)→M′(x′;y′)Da:M(x;y)→M′(x′;y′)

– Nếu a≡Ox⇒{x=x′y=−y′a≡Ox⇒{x=x′y=−y′

– Nếu a≡Oy⇒{x=−x′y=y′a≡Oy⇒{x=−x′y=y′

4. Phép đối xứng tâm

a. khái niệm

Cho điểm II. Phép biến hình biến điểm II thành chính nó, biến mỗi điểm MM khác II thành M′M′ sao cho II là trung điểm MM′MM′ được gọi là phép đối xứng tâm II. Kí hiệu: DIDI (II là tâm đối xứng)

DI(M)=M′⇔−−→IM′=−−−→IMDI(M)=M′⇔IM′→=−IM→

b. tính chất

– Nếu DI(M)=M′DI(M)=M′ và DI(N)=N′DI(N)=N′ thì −−−−→M′N′=−−−−→MNM′N′→=−MN→ , từ đó suy ra M′N′=MNM′N′=MN

– Phép đối xứng tâm biến đường thẳng thành đường thẳng {đồng thời|song song} hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nóm biến đường tròn thành đường tròn có cùng bán kính.

– Phép đối xứng tâm biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm {đổi mới|thay đổi} {thứ tự|trật tự} ba điểm đó.

– Phép đối xứng tâm bảo toàn khoảng cách giữa {hai|nhì|nhị} điểm bất kì.

c. Biểu thức tọa độ

Trong mặt phẳng tọa độ OxyOxy, cho I0(x0;y0)I0(x0;y0), gọi M(x;y)M(x;y) và M′(x′;y′)M′(x′;y′) với DI(M)=M′⇒{x′=2×0−xy′=2y0−yDI(M)=M′⇒{x′=2×0−xy′=2y0−y

5. Phép quay

a. Định nghĩa

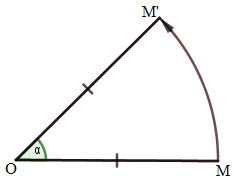
Trong mặt phẳng cho điểm OO {cố định|khăng khăng|một mực|nhất định|nhất mực|nhất quyết|nhất thiết} và góc lượng giác αα không đổi. Phép biến hình biến mỗi điểm MM

thành điểm M′M′ sao cho OM=OM′OM=OM′ và (OM,OM′)=α(OM,OM′)=α được gọi là phép quay tâm OO góc quay αα.

Kí hiệu: Q(O,α)Q(O,α)(OO là tâm phép quay, αα là góc quay lượng giác).

Q(O,α)(M)=M′⇔{OM=OM′(OM,OM′)=αQ(O,α)(M)=M′⇔{OM=OM′(OM,OM′)=α

b. tính chất

– Chiều dương của phép quay là chiều dương của đường tròn lượng giác (chiều kim đồng hồ).

– Với k∈Zk∈Z ta luôn có: Q(O,2kπ)Q(O,2kπ) là phép đồng nhất; Q(O,(2k+1)π)Q(O,(2k+1)π) là phép đối xứng tâm.

– Phép quay bảo toàn khoảng cách giữa {hai|nhì|nhị} điểm bất kì.

– Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

– Phép quay biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm {đổi mới|thay đổi} {thứ tự|trật tự}.

c. Biểu thức tọa độ

{x′−x0=(x−x0)cosφ−(y−y0)sinφy′−y0=(x−x0)sinφ+(y−y0)cosφ{x′−x0=(x−x0)cos⁡φ−(y−y0)sin⁡φy′−y0=(x−x0)sin⁡φ+(y−y0)cos⁡φ

Đặc biệt:

+) φ=90∘⇒{x′=−yy′=xφ=90∘⇒{x′=−yy′=x

+) Nếu φ=−90∘⇒{x′=yy′=−xφ=−90∘⇒{x′=yy′=−x

+) Nếu φ=180∘⇒{x′=−xy′=−yφ=180∘⇒{x′=−xy′=−y

6. Phép vị tự

a. Định nghĩa

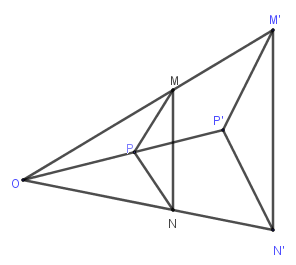
Cho điểm OO {cố định|khăng khăng|một mực|nhất định|nhất mực|nhất quyết|nhất thiết} và số k≠0k≠0 không đổi. Phép biến hình biến mỗi điểm MM thành điểm M′M′ sao cho −−−→OM′=k−−→OMOM′→=kOM→ được gọi là phép vị tự tâm O,O, tỉ số k.k.

Kí hiệu: V(O,k)V(O,k) (OO là tâm vị tự, kk là tỉ số vị tự)

V(o,k)(M)=M′⇔−−−→OM′=k−−→OMV(o,k)(M)=M′⇔OM′→=kOM→

b. tính chất

– Nếu phép vị tự tỉ số k biến {hai|nhì|nhị} điểm M,NM,N tùy ý theo {thứ tự|trật tự} thành M′,N′M′,N′ thì

−−−−→M′N′=k−−−→MNM′N′→=kMN→ và M′N′=|k|MNM′N′=|k|MN.

– Phép vị tự tỉ số k:k:

+ Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn {thứ tự|trật tự} giữa chúng.

+ Biến đường thẳng thành đường thẳng {đồng thời|song song} hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

+ Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

+ Biến đường tròn bán kính RR thành đường tròn có bán kính |k|.R|k|.R

c. Biểu thức tọa độ

Trong mặt phẳng tọa độ OxyOxy cho phép vị tự V(I,k)V(I,k) tâm I(x0;y0)I(x0;y0) biến điểm M(x;y)M(x;y) thành M′(x′;y′)M′(x′;y′).

Khi đó {x′=kx+(1−k)x0y′=ky+(1−k)y0{x′=kx+(1−k)x0y′=ky+(1−k)y0

7. Phép đồng dạng

a. Định nghĩa

Một phép biến hình FF được gọi là phép đồng dạng tỉ số k(k>0)k(k>0) nếu với {hai|nhì|nhị} điểm {bất cứ|bất kỳ} M,NM,N và ảnh M′,N′M′,N′ tương ứng của chúng ta luôn có M′N′=kMN.M′N′=kMN.

Nhận xét:

– Phép dời hình là phép đồng dạng tỉ số k=1k=1.

– Phép vị tự tỉ số kk là phép đồng dạng tỉ số |k||k|.

– Nếu {thực hành|thực hiện} {liên tiếp|liên tục} {hai|nhì|nhị} phép đồng dạng thì ta được một phép đồng dạng.

b. tính chất

– Phép đồng dạng tỉ số kk:

+ Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toán {thứ tự|trật tự} giữa chúng.

+ Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

+ Biến một tam giác thành tam giác đồng dạng với tam giác đã cho, biến góc thành góc bằng nó.

+ Biến một đường tròn bán kính RR thành đường tròn bán kính |k|.R|k|.R.

8. Phép dời hình và hai hình bằng nhau

– Phép dời hình là phép biến hình bảo toàn khoảng cách giữa {hai|nhì|nhị} điểm {bất cứ|bất kỳ}.

– {hai|nhì|nhị} hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.