Các góc của một tam giác và những giải thích chi tiết nhất

Chúng ta biết rằng mọi hình dạng trong vũ trụ đều dựa trên các góc độ. Hình vuông về cơ bản là bốn đường thẳng được nối với nhau theo cách mà mỗi đường tạo thành một góc 90 độ với đường kia. Theo cách này, một hình vuông có bốn góc 90 độ ở bốn cạnh của nó.

Tương tự, một đoạn thẳng kéo dài về hai phía một góc 180 độ, nếu nó quay tại một điểm bất kỳ thì nó sẽ trở thành hai đoạn thẳng cách nhau một góc nhất định. Theo cách tương tự, về cơ bản, tam giác là ba đường thẳng nối với nhau theo các giá trị nhất định của góc.

Các số đo góc này xác định loại tam giác. Do đó, các góc thực sự quan trọng trong việc nghiên cứu bất kỳ hình dạng hình học nào.

Trong bài này, bạn sẽ học các góc của một tam giác và cách tìm các góc chưa biết của một tam giác khi bạn chỉ biết một số góc. Để biết được các khái niệm quan trọng của tam giác, các bạn có thể tham khảo các bài viết trước.

Các góc của một tam giác là gì?

Góc của tam giác là không gian được tạo thành giữa độ dài hai cạnh của một tam giác. Một hình tam giác chứa các góc bên trong và góc bên ngoài. Góc trong là ba góc được tìm thấy bên trong một tam giác. Góc ngoại tiếp được hình thành khi các cạnh của tam giác được kéo dài đến vô cùng.

Do đó, các góc bên ngoài là các góc được tạo thành bên ngoài một tam giác nằm giữa, một cạnh của tam giác và cạnh kéo dài. Mỗi góc bên ngoài tiếp giáp với một góc bên trong. Góc kề là góc có đỉnh và cạnh chung.

Hình dưới đây cho thấy góc của một tam giác . Các góc bên trong là a, b và c, trong khi các góc bên ngoài là d, e và f.

Làm thế nào để tìm các góc của một tam giác?

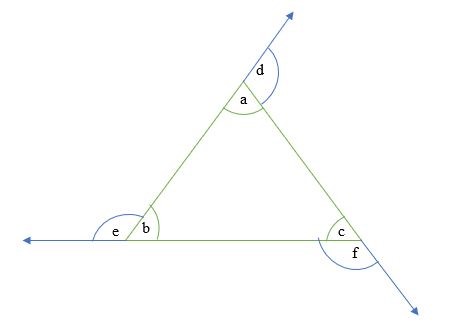
Để tìm các góc của hình tam giác, bạn cần nhớ lại ba tính chất sau đây về hình tam giác:

• Định lý tổng góc tam giác: Phát biểu rằng tổng ba góc trong của tam giác bằng 180 độ.

a + b + c = 180º

• Định lý góc ngoại tiếp tam giác: Phát biểu rằng góc bên ngoài bằng tổng hai góc đối diện và không kề.

f = b + a

e = c + b

d = b + c

• Các góc đường thẳng. Số đo các góc trên đường thẳng bằng 180º

c + f = 180º

a + d = 180º

e + b = 180º

Chúng ta hãy tìm ra một vài vấn đề ví dụ.

ví dụ 1

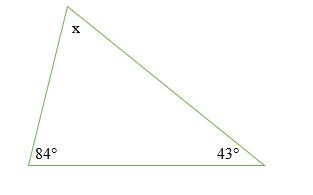
Tính độ lớn của góc khuyết x trong tam giác dưới đây.

Giải pháp

Theo định lý tổng góc tam giác, ta có,

x + 84º + 43º = 180º

Đơn giản hóa.

x + 127º = 180º

Trừ 127º cho cả hai bên.

x + 127º – 127º = 180º – 127º

x = 53 º

Do đó, kích thước của góc bị thiếu là 53º.

Ví dụ 2

Tìm kích thước của các góc trong của một tam giác tạo thành các số nguyên dương liên tiếp.

Giải pháp

Vì một tam giác có ba góc trong nên các góc liên tiếp là:

⇒1 góc ^ST = x

⇒ Góc 2 ^ND = x + 1

⇒3 Góc ^RD = x + 2

Nhưng chúng ta biết rằng, tổng của ba góc bằng 180 độ, do đó,

⇒ x + x + 1 + x + 2 = 180 °

⇒ 3x + 3 = 180 °

⇒ 3x = 177 °

x = 59 °

Bây giờ, thay giá trị của x vào ba phương trình ban đầu.

⇒ 1 góc ^ST = x = 59 °

⇒ Góc 2 ^ND = x + 1 = 59 ° + 1 = 60 °

⇒3 Góc ^RD = x + 2 = 59 ° + 2 = 61 °

Vậy, các góc nội tiếp liên tiếp của tam giác là; 59 °, 60 ° và 61 °.

Ví dụ 3

Tìm các góc trong của một tam giác có các góc đã cho là; 2y °, (3y + 15) ° và (2y + 25) °.

Giải pháp

Trong tam giác, um của các góc bên trong = 180 °

2y ° + (3y + 15) ° + (2y + 25) ° = 180 °

Đơn giản hóa.

2y + 3y + 2y + 15 ° + 25 ° = 180 °

7y + 40 ° = 180 °

Trừ 40 ° cho cả hai bên.

7y + 40 ° – 40 ° = 180 ° – 40 °

7y = 140 °

Chia cả hai bên cho 7.

y = 140/7

y = 20 °

Thay thế,

2y ° = 2 (20) ° = 40 °

(3y + 15) ° = (3 x 20 + 15) ° = 75 °

(2y + 25) ° = (2 x 20 + 25) ° = 65 °

Vì vậy, ba góc trong của một tam giác là 40 °, 75 ° và 65 °.

 Ví dụ 4

Tìm giá trị của các góc còn thiếu trong sơ đồ dưới đây.

Giải pháp

Theo định lý góc ngoại tiếp tam giác, ta có;

(2x + 10) ° = 63 ° + 87 °

Đơn giản hóa

2x + 10 ° = 150 °

Trừ 10 ° cho cả hai bên.

2x + 10 ° – 10 = 150 ° – 10

2x = 140 °

Chia cả hai vế cho 2 để được;

x = 70 °

Bây giờ, bằng cách thay thế;

(2x + 10) ° = 2 (70 °) + 10 ° = 140 ° + 10 ° = 150 °

Do đó, góc bên ngoài là 150 °

Tuy nhiên, góc của đường thẳng cộng lại lên đến 180 °. Vì vậy chúng tôi có;

y + 150 ° = 180 °

Trừ 150 ° cho cả hai bên.

y + 150 ° – 150 ° = 180 ° – 150 °

y = 30 °

Do đó, các góc bị thiếu là 30 ° và 150 °.

Ví dụ 5

Các góc trong của một tam giác theo tỷ lệ 4: 11: 15. Tìm các góc.

Giải pháp

Gọi x là tỉ số chung của ba góc. Vì vậy, các góc,

4x, 11x và 15x.

Trong một tam giác, tổng ba góc = 180 °

4x + 11x + 15x = 180 °

Đơn giản hóa.

30x = 180 °

Chia 30 cho cả hai bên.

x = 180 ° / 30

x = 6 °

Thay thế giá trị của x.

4x = 4 (6) ° = 24 °

11x = 11 (6) ° = 66 °

15x = 15 (6) ° = 90 °

Vì vậy, các góc của tam giác là 24 °, 66 ° và 90 °.

Ví dụ 6

Tìm kích thước của góc x và y trong sơ đồ dưới đây.

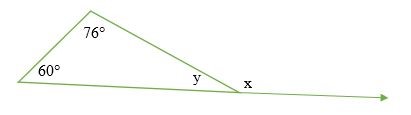
Giải pháp

Góc ngoại thất = tổng của hai góc nội thất không kề nhau.

60 ° + 76 ° = x

x = 136 °

Tương tự, tổng các góc bên trong = 180 °. Vì thế,

60 ° + 76 ° + y = 180 °

136 ° + y = 180 °

Trừ 136 ° cho cả hai bên.

136 ° – 136 ° + y = 180 ° – 136

y = 44 °

Do đó, kích thước của góc x và y lần lượt là 136 ° và 44 °.

Ví dụ 7

Ba góc của một tam giác nào đó sao cho góc thứ nhất nhỏ hơn góc thứ hai 20% và góc thứ ba hơn góc thứ hai 20%. Tìm kích thước của ba góc.

Giải pháp

Gọi góc thứ hai là x

Góc đầu tiên = x – 20x / 100 = x – 0,2x

Góc thứ ba = x + 20x / 100 = x + 0,2x

Tổng của ba góc = 180 độ.

x + x – 0. 2x + x + 0.2x = 180 °

Đơn giản hóa.

3x = 180 °

x = 60 °

Vì thế,

2 ^nd góc thứ hai = 60 °

1 ^st góc = 48 °

3 ^thứ góc = 72 °

Vì vậy, ba góc của một tam giác là 60 °, 48 ° và 72 °.

Ví dụ 8

Tính độ lớn của góc p, q, r và s trong sơ đồ dưới đây.

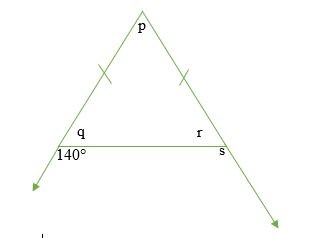
Giải pháp

góc bên ngoài = tổng của hai góc bên trong không kề nhau.

140 ° = p + r …………. (Tôi)

Đây là một tam giác cân, vì vậy,

q = r

Các góc trên một đường thẳng = 180 °

140 ° + q = 180 °

trừ 140 cho cả hai bên để có được.

q = 40 °

Nhưng q = r, do đó r cũng là 40 °

r + s = 180 ° (góc tuyến tính)

40 ° + s = 180 °

s = 140 °

Tổng các góc bên trong = 180 °

p + q + r = 180 °

p + 40 ° + 40 ° = 180 °

p = 180 ° – 80 °

p = 100 °

Xem thêm:

Bất đẳng thức tam giác là gì và những ví dụ điển hình nhất

Bộ ba Pitago và những thông tin liên quan mới nhất về nó