Quy tắc sin và những quy tắc tính toán vô cùng đơn giản

Bây giờ khi bạn đã xem qua các góc và các cạnh của hình tam giác và các tính chất của chúng, bây giờ chúng ta có thể chuyển sang quy tắc rất quan trọng. Chúng ta thấy rằng một góc khuyết của một tam giác có thể dễ dàng tính được khi chúng ta cho hai góc khác, vì chúng ta biết rằng tổng tất cả các góc của một tam giác bằng 180 độ.

Nhưng làm thế nào bạn sẽ tìm thấy một góc bị thiếu khi bạn chỉ được cung cấp một góc và hai cạnh hoặc làm thế nào bạn sẽ tìm thấy một cạnh bị thiếu khi bạn được cung cấp cho hai góc và một cạnh?

Đó là nơi mà sự nhầm lẫn bắt đầu!

Nhưng đừng lo lắng, các nhà toán học của 11 ^thứ thế kỷ, Ibn al-Muaadh Jayyani, tìm ra giải pháp trong cuốn sách của ông “Cuốn sách của vòng cung không rõ của một quả cầu”.

Ông đã trình bày một vị tướng Luật Sines , được lấy thêm bằng Nasir al-Din trong 13 ^thứ thế kỷ. Ông đã trình bày Định luật Sines cho các tam giác phẳng và hình cầu, rất quan trọng trong việc tính toán các thông số của tam giác. Cùng với đó, anh cũng đưa ra những dẫn chứng về điều luật này.

Trong bài viết này, bạn sẽ tìm hiểu về:

• Luật của sin,
• luật của công thức sin, và
• làm thế nào để làm luật của sines.

Luật Sines là gì?

Luật sin hay đôi khi được gọi là quy tắc sin là một quy tắc liên hệ các cạnh của một tam giác với sin của các góc đối diện của chúng.

Trước khi tiếp tục với luật sin, trước tiên chúng ta hãy hiểu ý nghĩa của thuật ngữ sin .

Xét tam giác vuông ABC dưới đây.

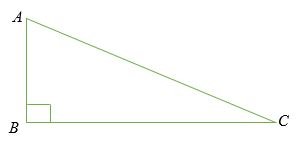
Cho biết AC là cạnh huyền của tam giác vuông ABC thì sin của góc BCA bằng tỉ số độ dài AB với độ dài AC.

Hình sin < BCA = AB / AC

Tương tự, sin của góc BAC bằng tỉ số độ dài BC và độ dài AC .

Hình sin < BAC = BC / AC

Do đó, sin của một góc là tỷ số giữa độ dài cạnh đối diện của góc với độ dài cạnh huyền.

Bây giờ, hãy xem xét một tam giác ABC xiên được hiển thị bên dưới. Một tam giác xiên là không có góc vuông (tam giác không có góc 90 độ). Ba góc của tam giác này được ký hiệu bằng chữ in hoa trong khi các cạnh đối diện được ký hiệu bằng chữ thường. Lưu ý rằng mỗi cạnh và góc đối diện của nó có cùng một chữ cái.

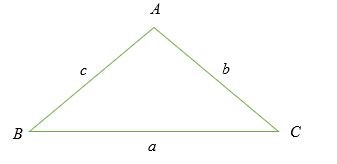
Theo luật ô sin.

a / Sin (A) = b / Sin (B) = c / Sin (C)

Một ứng dụng thực tế của quy tắc sin là thanh sin, được sử dụng để đo góc nghiêng trong kỹ thuật.

Các ví dụ phổ biến khác bao gồm đo khoảng cách trong điều hướng và đo khoảng cách giữa hai ngôi sao trong thiên văn học.

Công thức quy tắc sin?

Công thức luật sin được đưa ra bởi

a / Sine (A) = b / Sine (B) = c / Sine (C) hoặc Sine (A) / a = Sine (B) / b = Sine (C) / c

trong đó a, b, c lần lượt là độ dài các cạnh đối diện với các góc A, B và C.

Làm thế nào để Thực hiện Luật Sines?

Định luật sin có thể được sử dụng để tính cả các cạnh của một tam giác và các góc của một tam giác.

Nếu bạn muốn tính độ dài của một cạnh, bạn cần sử dụng phiên bản của quy tắc sin trong đó độ dài là tử số:

a / Sine (A) = b / Sine (B) = c / Sine (C)

Bạn sẽ chỉ cần hai phần của công thức quy tắc sin, không phải cả ba. Bạn sẽ cần biết ít nhất một cặp cạnh với góc đối diện của nó.

Nếu bạn muốn tính kích thước của một góc, bạn cần sử dụng phiên bản của quy tắc sin trong đó các góc là tử số.

Sine (A) / a = Sine (B) / b = Sine (C) / c

Như trước đây, bạn sẽ chỉ cần hai phần của quy tắc sin và bạn vẫn cần ít nhất một cạnh và góc đối diện của nó.

Hãy giải quyết một số vấn đề ví dụ dựa trên quy tắc sin.

ví dụ 1

Cho rằng sin (A) = 2/3, hãy tính góc ∠ B như hình bên dưới.

Giải pháp

Vì chúng ta được yêu cầu tính kích thước của một góc, nên chúng ta sẽ sử dụng quy tắc sin trong biểu mẫu;

Sine (A) / a = Sine (B) / b

Bằng cách thay thế,

(2/3) / 2 = sin (B) / 3

3 (2/3) = 2 sin B

2 = 2 sin B

Chia cả hai bên cho 2

1 = sin B

Tìm nghịch đảo sin của 1 bằng máy tính khoa học.

Sin ^-1 1 = B

Do đó, ∠B = 90˚

Ví dụ 2

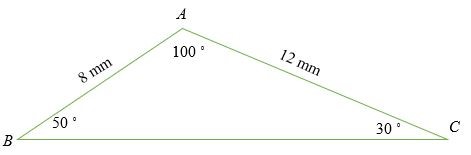
Tính độ dài cạnh BC của hình tam giác dưới đây.

Giải pháp

Bởi vì, chúng ta cần tính độ dài của cạnh, do đó chúng ta sử dụng quy tắc sin ở dạng

a / sin (A) = b / sin (B)

Bây giờ thay thế.

a / sin 100 ˚ = 12 / sin 50 ˚

Nhân chéo.

12 sin 100 ˚ = a sin 50 ˚

Chia cả hai bên cho sin 50 ˚

a = (12 sin 100 ˚) / sin 50 ˚

Bằng cách sử dụng một máy tính, chúng tôi nhận được;

a = 15,427

Như vậy, chiều dài cạnh BC là 15,427 mm.

Ví dụ 3

Tính độ dài còn thiếu của tam giác sau.

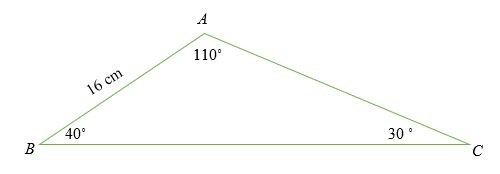
Giải pháp

a / sin (A) = b / sin (B) = c / sin (C)

Bằng cách thay thế, chúng tôi có,

a / sin 110 ˚ = 16 / sin 30 ˚

Nhân chéo

a = (16 sin 110 ˚) / sin 30 ˚

a = 30,1

Giải quyết cho b.

b / sin 40 ˚ = 16 / sin 30 ˚

b = (16 sin 40 ˚) / sin 30 ˚

= 20,6

Do đó, độ dài BC = 30. 1 cm và độ dài AC = 20,6 cm.

Xem thêm: 

Hình tam giác vuông đặc biệt – Giải thích & Ví dụ hay nhất

Quy tắc Cosine và những cách giải hay nhất hiện nay

Ví dụ 4

Tính các góc của tam giác dưới đây.

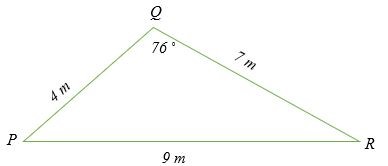
Giải pháp

Áp dụng quy tắc sin trong biểu mẫu;

sin (Q) / q = Sine (P) / p = sin R / r

(Sin 76 ˚) / 9 = sin (P) / 7

Giải cho góc P

Nhân chéo.

7 sin 76 ˚ = 9 sin P

Chia cả hai bên cho 9

Sin P = 7/9 sin 76 ˚

Sin P = 0,7547

Tìm nghịch đảo của sin của 0,7547.

Sin ^-1 0,7547 = P

P = 48,99 ˚

Giải cho góc R

Sine R / 4 = Sine 76 ˚ / 9

Nhân chéo.

9 sin R = 4 sin 76 ˚

Chia cả hai bên cho 9

Sin R = 4/9 sin 76 ˚

Sin R = 0,43124.

Sin ^-1 0,43124 = R

R = 25,54 ˚