Cách tính diện tích hình thang

Các bài toán liên quan đến hình thang thường rất phổ biến và học sinh cần phải làm quen với các kiến thức về hình thang từ rất sớm. Tuy nhiên, cách tính diện tích hình thang cũng gây không ít khó khăn cho các học sinh bởi sự phân hóa nhiều loại hình thang. 

Với bài viết này, tintuctuyensinh sẽ giúp bạn thống kê lại một cách đầy đủ nhất các công thức tính diện tích hình thang. Đây đều là những công thức thường gặp trong các bài tập sách giáo khoa từ cấp tiểu học đến trung học phổ thông. 

1.HÌNH THANG LÀ GÌ?

Theo hình học Euclide, hình thang là một tứ giác lồi có hai cạnh đối song song. Hai cạnh đáy chính là hai cạnh song song của hình thang trong khi hai cạnh còn lại là các cạnh bên của hình.

Công thức tính chu vi hình thang khá đơn giản, bạn chỉ cần cộng tất cả 4 cạnh của hình vào nhau. Tuy nhiên, công thức tính diện tích lại có phần phức tạp hơn do có tới 3 loại hình thang với các công thức tính diện tích khác nhau: 

• Hình thang vuông
• Hình thang thường
• Hình thang cân

1. Hình thang thường

định nghĩa: Hình thang là một tư giác lồi có hai cạnh đáy đồng thời, 2 cạnh còn lại được gọi là nhị cạnh bên.

– Công thức tính diện tích hình thang thường

Diện tích hình thang bằng nhàng nhàng cộng của 2 đáy nhân với chiều cao của nó.

S = h x ((a +b)/2)

Trong đó:

+ S: Diện tích.

+ a,b: tuần tự là độ dài 2 đáy.

+ h: Chiều cao hình thang.

thí dụ:

Một hình thang có chiều cao = 4cm, đáy nhỏ nhắn a = 5cm, đáy to b = 12cm. Diện tích hình thang trên?

vận dụng công thức S = h x ((a +b)/2) = 4 x ((5+12)/2)= 34 (cm).

Còn có bài thơ về tính diện tích hình thang khá dễ nhớ như sau:

Muốn tính diện tích hình thang

Đáy phệ đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra.

– Công thức tính chu vi hình thang

Chu vi hình thang bằng tổng các cạnh bên và cạnh đáy.

P= a + b + c + d.

Trong đó:

+ P: Chu vi hình thang.

+ a,b: lần lượt là độ dài 2 cạnh đáy.

+ c,d: lần lượt là đội dài 2 cạnh bên.

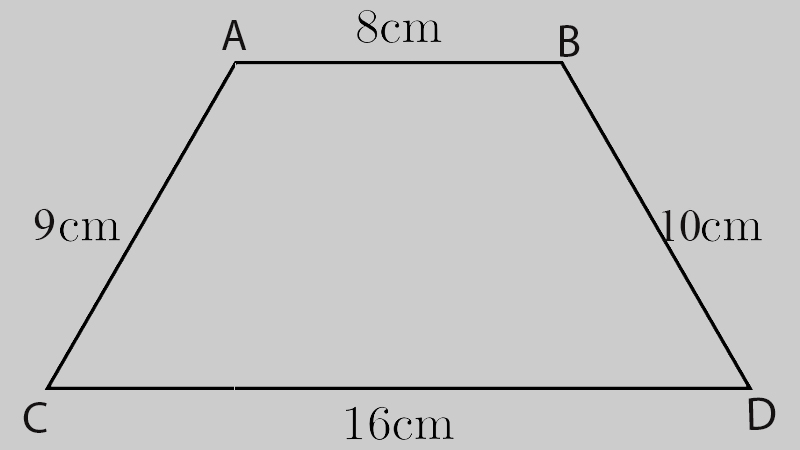
Một hình thang có độ dài các cạnh bên lần lượt là 8cm, độ dài đáy nhỏ nhắn, đáy to tuần tự là 8cm, 16cm. Hãy tính chu vi hình thang nói trên?

Ta có công thức: P = a + b + c + d = 8 + 8 + 8 +16 = 40cm.

– Công thức tính diện tích hình thang khi biết độ dài 4 cạnh

Ta có công thức như sau:

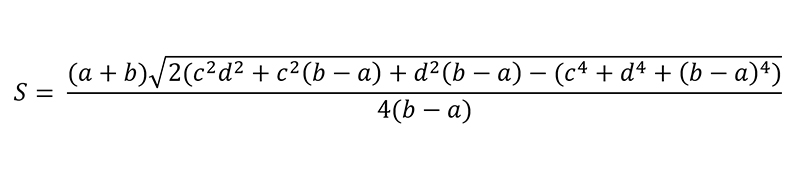
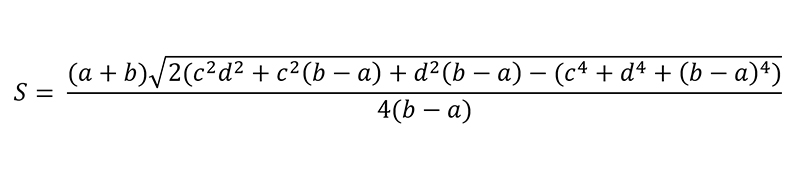
Trong đó:

+ a,b: lần lượt là độ dài 2 cạnh đáy.

+ c,d: lần lượt là đội dài 2 cạnh bên.

2. Hình thang vuông

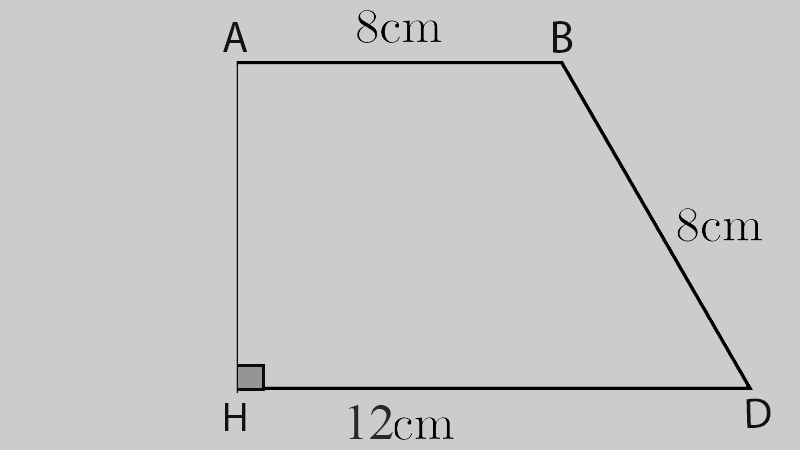
khái niệm: Hình thang vuông là một dạng đặc biệt của hình thang. Hình thang vuông có nhì góc vuông, có chiều cao đồng thời là cạnh bên vuông góc với hai cạnh đáy.

Công thức tính diện tích hình thang vuông

S = h x ((a + b)/2)

Trong đó:

+ S: Diện tích.

+ a,b: tuần tự là độ dài 2 đáy.

+ h: Chiều cao hình thang.

Một hình thang vuông ABHD có độ dài đáy bé bỏng đáy lớn tuần tự là 8cm, 12cm. Trong đó có cạnh AH = 8cm. Hãy tính diện tích hình thang vuông đó.

ứng dụng công thức: S = h x ((a + b)/2) = 8 x ((8 + 12)/ 2) = 80cm.

3. Hình thang cân

khái niệm: Hình thang cân là hình có nhị cạnh bên bằng nhau, nhì góc tạo bởi cạnh bên và cạnh đáy bằng nhau.

Công thức tính diện tích hình thang cân

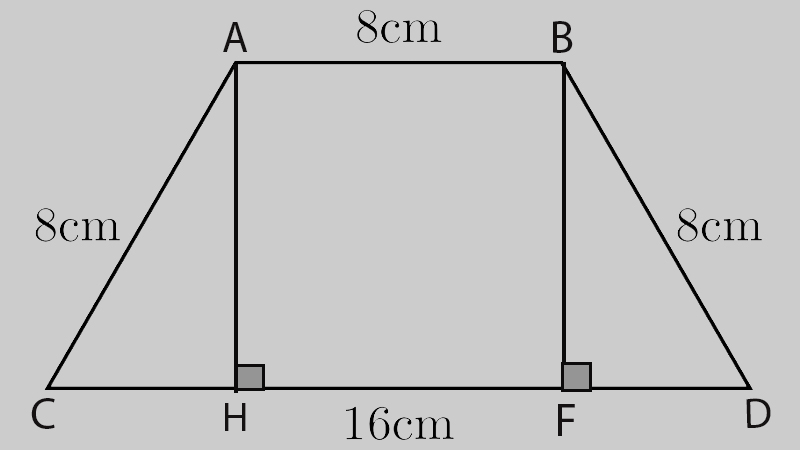
Để tính diện tích hình thang cân, chúng ta có thể tính theo công thức tổng quát ở trên hoặc chia hình thang cân thành 1 hình vuông và 2 tam giác vuông, tính diện tích từng hình rồi cộng chúng lại.

S = h x ((a + b)/2).

Trong đó:

+ S: diện tích.

+ a,b: tuần tự là độ dài 2 đáy.

+ h: chiều cao hình thang.

Ví dụ: S = h x ((a + b)/2) = 8 x ((8+16)/2) = 96cm.

S = 2 x S.ACH + S.ABHF = 2 x 1/2 x 8 x 4 + 8 x 8 = 96cm.

4. Những chú ý khi tính diện tích, chu vi hình thang

để ý đổi doanh nghiệp chiều dài các cạnh hình thang.

Trong quá trình giải toán, nhiều khi Anh chị sẽ thắc bận bịu hình thang có thể tích hay không? Thì câu giải đáp là không. vì căn bản hình thang là hình học nhị chiều, nên chẳng thể tính thể tích hình thang.

Phần dưới là các bạn xem thêm thôi

4. CÁCH TÍNH DIỆN TÍCH HÌNH THANG THƯỜNG

Hình thang thường là loại hình thang mang đúng những đặc điểm kể trên của hình thang và không có thêm các điểm đặc biệt nào khác. 

Cách tính diện tích hình thang thường: trung bình cộng 2 cạnh đáy nhân với chiều cao của hình thang. 

Giả sử, ta có hình thang ABCD với chiều dài hai đáy AB, CD lần lượt là a,b. Chiều cao giữa hai đáy AH = h. DIện tích hình thang ABCD có thể tính như sau:

Trong đó: 

• Diện tích hình thang là S
• Độ dài 2 đáy lần lượt là a, b
• Độ dài chiều cao hình thang là h

Cách tính diện tích hình thang còn được “tổng quát” bằng cả một bài thơ. Giúp bạn học thuộc công thức dễ dàng hơn rất nhiều: 

Để tính diện tích hình thang

Đáy lớn đáy nhỏ bạn đem cộng vào

Rồi nhân với cả đường cao

Chia đôi kết quả thế nào cũng ra

2. CÁCH TÍNH DIỆN TÍCH HÌNH THANG VUÔNG

Trong hình học Euclide, hình thang vuông là một trường hợp đặc biệt của hình thang và có 1 góc vuông. Cạnh bên vuông góc với đáy đóng luôn vai trò là chiều cao của hình thang. 

Từ công thức diện tích hình thang tường, ta có công thức diện tích hình thang vuông khá tương tự. Chỉ khác ở chỗ chiều cao hai đáy nay tương ứng với chính cạnh bên vuông góc với hai đáy.

Trong đó: 

• Diện tích hình thang là S
• Độ dài 2 cạnh đáy lần lượt là a,b
• Độ dài cạnh bên vuông góc 2 đáy là h (đóng vai trò như chiều cao) 

5.DIỆN TÍCH HÌNH THANG CÂN

Hình thang có 2 góc kề 1 đáy bằng nhau được gọi là hình thang cân. Cạnh bên trong hình thang cân cũng bằng nhau và 2 cạnh không song song với nhau.

Để tính diện tích hình thang cân, học sinh có thể áp dụng trực tiếp công thức tính hình thang như bình thường. Hoặc bạn có thể tham khảo cách chia nhỏ hình thang cân để tính diện tích từng phần, sau đó cộng lại với nhau..

Lấy ví dụ hình thang cân ABCD có AD và BC bằng nhau. Đường cao AH và BK của ABCD chia hình thang ra thành hình chữ nhật ABKH và 2 hình tam giác ADH và BCK. Từ đây ta dễ dàng áp dụng công thức tính diện tích hình chữ nhật để tính diện tích ABHK, diện tích tam giác cho ADH và BCK (có diện tích bằng nhau). Tổng các diện tích này chính là diện tích hình thang cân ABCD cần tìm.  

Mà SADH = SBCK , vì thế ta có:

6.CÁCH TÍNH DIỆN TÍCH HÌNH THANG KHI BIẾT ĐỘ DÀI 4 CẠNH

Ở các cấp học lớn hơn, cách tính diện tích hình thang cũng trở nên phức tạp hơn. Có một vài bài toán yêu cầu tính diện tích hình thang khi chỉ biết độ dài 4 cạnh, không cho biết chiều cao. 

Với các bài toán dạng này, khi bạn biết rõ độ dài 4 cạnh và đâu là cạnh đáy thì rất dễ dàng tính được diện tích hình thang. Giả sử hình thang có Q, P lần lượt là chiều dài cạnh đáy, R và S là chiều dài 2 cạnh bên. Trong đó P lớn hơn Q. 

Ta có công thức hình thang như sau:

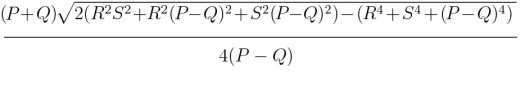
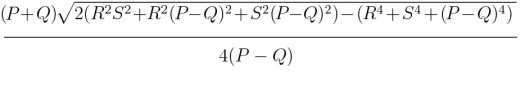
Bài toán tính diện tích hình thang khi biết chiều dài 4 cạnh cũng có thể làm bằng cách tách hình thang thành 2 tam giác và 1 hình chữ nhật. 

Một cách khác nữa là kẻ thêm chiều cao hình thang giữa 2 cạnh bên, từ đó áp dụng công thức Heron tính diện tích tam giác. Từ đó tính được diện tích hình thang cần tìm. Cụ thể công thức Heron như sau: Giả sử S là diện tích tam giác và độ dài 3 cạnh lần lượt là a, b, c. p được ký hiệu là nửa chu vi của tam giác. 

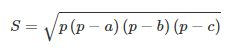
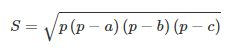
Các cách viết lại khác của công thức Heron có thể kể đến như:

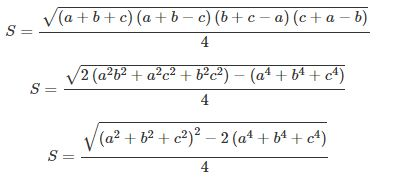
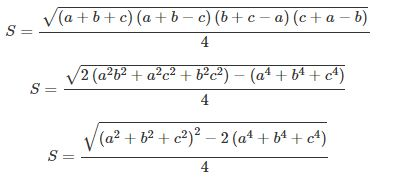
Trên đây là bài tổng hợp các cách tính diện tích hình thang từ cơ bản đến phức tạp.Nắm chắc công thức tính hình thang giúp ích rất nhiều trong việc học hình học nói riêng và toán học nói chung của các bạn học sinh. tintuctuyensinh hy vọng bạn đã nắm vững hết các cách tính diện tích hình thang qua bài viết này và có kết quả học tập tốt nhất trong thời gian ôn tập này nhé.