Phương trình Elip

Phương trình Elip

khái niệm

Cho 2 điểm nhất thiết F₁, F_2­ và một độ dài không đổi 2a lớn hơn F₁F₂. Elip là tụ hội các điểm M trong mặt phẳng sao cho F₁M + F₂M = 2a

Các điểm F₁ và F₂ gọi là tiêu điểm của Elip. Độ dài F­₁F₂ = 2c gọi là tiêu cự của Elip.

Phương trình chính tắc của Elip (E)

Cho Elip (E) có các tiêu điểm F₁(-c; 0) và F₂(c; 0). Điểm M thuộc Elip khi và chỉ khi MF₁ + MF₂ = 2a.

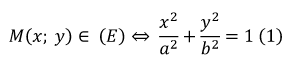
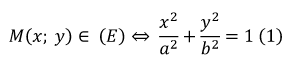
Trong đó: b² = a² – c²

Phương trình (1) được gọi là phương trình chính tắc của Elip (E)

Xét Elip (E) có phương trình (1):

Nếu điểm M(x; y) thuộc (E) thì các điểm M₁(-x; y), M₂(x; -y) và M₃(-x; -y) cũng thuộc (E).

do đó (E) có các trục đối xứng là Ox, Oy và có tâm đối xứng là gốc O

Thay y = 0 vào (1) ta có: x = ± a, suy ra (E) cắt Ox tại 2 điểm A₁(-a; 0) và A₂(a; 0)

Thay x = 0 vào (1) ta có: y = ± b, suy ra (E) cắt Oy tại 2 điểm B₁(0; -b) và A₂(0; b)

Các điểm A­₁, A₂, B₁, B₂ gọi là các đỉnh của elip

Đoạn thẳng A₁A₂ gọi là trục phệ, đoạn thẳng B₁B₂ gọi là trục nhỏ dại của elip

Xem thêm: Lý thuyết Vị trí tương đối của hai đường tròn

Các thành phần của phương trình Elip

– nhị tiêu điểm: F₁(-c; 0) và F₂(c; 0)

– bốn đỉnh: A₁(-a; 0), A₂(a; 0), B₁(-b; 0), B₂(b; 0)

– Độ dài trục lớn: A₁A₂ = 2a

– Độ dài trục nhỏ: B₁B₂ = 2b

– Tiêu cự: F­₁F₂ = 2c

Các dạng bài tập và lý lẽ giải

Dạng 1: Lập phương trình chính tắc của một elip khi biết các thành phần đủ để xác định elip đó

Phương pháp:

• Từ các thành phần đã biết, vận dụng công thức thúc đẩy, ta tìm được phương trình chính tắc của elip.
• Lập phương trình chính tắc của Elip theo công thức:

• Ta có các hệ thức:

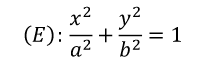
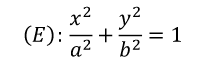
– 0 < b < a

– c² = a² – b²

– Độ dài trục lớn: A₁A₂ = 2a

– Độ dài trục nhỏ: B₁B₂ = 2b

– Tiêu cự: F­₁F₂ = 2c

– MF₁ + MF₂ = 2a

• Ta có tọa độ các điểm khác lạ của Elip (E)

– nhị tiêu điểm: F₁(-c; 0) và F₂(c; 0)

– tư đỉnh: A₁(-a; 0), A₂(a; 0), B₁(-b; 0), B₂(b; 0)

Dạng 2: Xác định các thành phần của một Elip khi biết phương trình chinh tắc của Elip đó

Phương pháp:

Từ đó tính cách thành phần theo các hệ thức của dạng 1.

Trên đây là những kiến thức về phương trình Elip. Nhìn bình thường các kiến thức này khá dễ nhớ, cho nên hãy nỗ lực nắm vững để giải các bài tập phần này nhé!