Contents
Cặp phương trình tuyến tính trong ghi chú hai biến
Trong các lớp trước, chúng ta đã nghiên cứu về phương trình tuyến tính trong một biến và chúng ta biết cách giải nó. Nếu có một biến và một phương trình, chúng ta thường giải nó một cách dễ dàng, nhưng trong trường hợp này, chúng ta có hai biến và hai phương trình. Một điều chắc chắn là chúng ta cần hai bộ phương trình tuyến tính khác nhau để tìm ra hai ẩn số khác nhau. Nếu một phương trình được đưa ra và hai biến được yêu cầu giải, chúng ta sẽ không nhận được nghiệm cụ thể.
Ví dụ,
3x + 2y = 9 và 5x + y = 10
Những phương trình đồng thời này có thể được giải quyết và chúng ta có thể đi đến một giải pháp cụ thể từ những phương trình này nhưng mặt khác,
6x + 7y = 9
Ở đây, chúng ta không thể có một giải pháp cụ thể cho điều này vì chỉ có một điều kiện được đưa ra và chúng ta có hai ẩn số. Chúng ta có thể viết lại phương trình trên thành:
y = (9-6x) / 7
Tùy thuộc vào các giá trị của x, các giá trị của y sẽ thay đổi tương ứng. Vì vậy, một giải pháp duy nhất là không thể.
Như vậy, có thể nói rõ ràng rằng để có được một nghiệm cụ thể của hệ, của phương trình tuyến tính hai biến, chúng ta cần hai tập điều kiện độc lập khác nhau.
Biểu diễn cặp phương trình tuyến tính trong hai biến
Cặp phương trình tuyến tính có thể được giải và biểu diễn bằng hai phương pháp:
- Phương pháp đồ họa
- Phương pháp đại số
Biểu diễn tổng quát của một cặp phương trình tuyến tính theo hai biến cho biết x và y được cho bởi:
a 1 x + b 1 y + c 1 = 0 …………… (1)
a 2 x + b 2 y + c 2 = 0 …………… (2)
trong đó a 1 , b 1 , c 1 , a 2 , b 2 , c 2 đều là các số thực và a 1 2 + b 1 2 ≠ 0, a 2 2 + b 2 2 ≠ 0.
Nếu cặp phương trình tuyến tính được cho dưới dạng a 1 x + b 1 y + c 1 = 0 và a 2 x + b 2 y + c 2 = 0, thì ở đây xuất hiện ba điều kiện:
- Nếu cặp phương trình tuyến tính là nhất quán thì: a 1 / a 2 ≠ b 1 / b 2
- Nếu cặp phương trình tuyến tính không đồng nhất thì: a 1 / a 2 = b 1 / b 2 ≠ c 1 / c 2
- Nếu cặp phương trình tuyến tính phụ thuộc và nhất quán thì: a 1 / a 2 = b 1 / b 2 = c 1 / c 2
Ví dụ, 2x-y = -1 và 3x + 2y = 9 là cặp phương trình tuyến tính với các biến x và y. Trong sơ đồ dưới đây, bạn có thể thấy chúng ta đã tìm ra nghiệm cho cả hai phương trình bằng cách đặt giá trị của x để nhận giá trị của y.
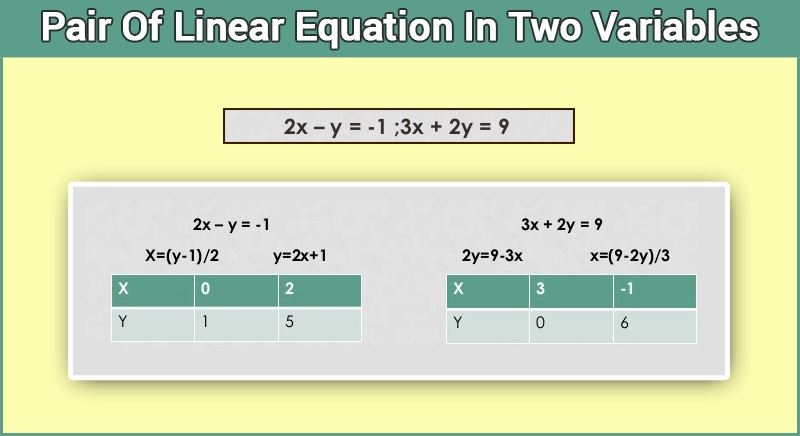

Theo cách tương tự, chúng ta có thể tìm giải pháp cho các ví dụ sau:
- 2x + 3y-4 = 0 và 3x + 2y + 4 = 0
- 6x = y và 4x-3y-5 = 0
Nhưng điều gì sẽ xảy ra nếu chúng ta phải biểu diễn các phương trình này trong đồ thị. Hãy cùng chúng tôi tìm hiểu trong phần tiếp theo.
Biểu diễn đồ họa
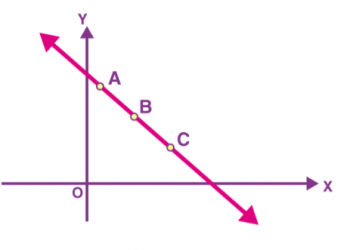
Bạn đã học ở Lớp 9, nếu có hai đường thẳng trong một mặt phẳng, thì có thể có ba khả năng xảy ra, chẳng hạn như;
- Hai đường thẳng cắt nhau
- Hoặc chúng song song với nhau
- Hoặc họ trùng hợp với nhau
Ba điều kiện trên có thể được biểu diễn bằng đồ thị như hình dưới đây:


Bây giờ chúng ta hãy xem xét một cặp phương trình tuyến tính, x + y = 5, 2x + 2y = 10. Để biểu diễn hai phương trình tuyến tính này trong một đồ thị bằng một đường thẳng, trước tiên, chúng ta cần tìm nghiệm. Sau khi tìm các nghiệm, chúng ta nhận được các giá trị phân biệt của x và y. Do đó, nó có thể được biểu diễn dưới dạng:


Phương pháp đại số giải một cặp phương trình tuyến tính
Chúng ta hãy bắt đầu với ứng dụng thực tế của phương trình tuyến tính đồng thời trong cuộc sống hàng ngày của chúng ta. Cặp phương trình tuyến tính có thể tìm thấy đường đi của nó trong mọi trường hợp có thể xảy ra. Nói rằng bạn đã đến chợ cá để mua cá. Có hai kích cỡ cá có sẵn. Người câu cá nói rằng tổng giá của con cá nhỏ gấp 3 lần tổng giá của con cá lớn hơn. Ngoài ra, tổng số tiền bạn đã mua từ ngôi nhà của mình là 100 Rs. Bạn có thể tìm hiểu xem bạn đã bỏ ra bao nhiêu để mua hai loại cá?
Hãy để chúng tôi hiểu điều này một cách toán học,
Đặt giá của con cá nhỏ hơn là Rs.x và giá của con cá lớn hơn là Rs.y.
Theo điều kiện đầu tiên, x = 3y ………… (1)
Và theo điều kiện thứ hai, x + y = 100 …………… (2)
Để tìm được nghiệm, chúng ta cần giải cả hai phương trình và tìm giá trị của cả x và y. Các tọa độ (x, y) có thể được đặt dễ dàng trong đồ thị. Nhưng phương pháp đồ thị không thuận tiện trong trường hợp điểm biểu diễn nghiệm của phương trình tuyến tính có tọa độ không tích phân như ( √ 3, 2 √ 7), (–1,75, 3,3), (4/13, 1/18) , vv Do đó, chúng tôi sử dụng phương pháp đại số để giải quyết các trường hợp như vậy.
Có các loại phương pháp đại số sau để giải một cặp phương trình tuyến tính:
- Phương pháp thay thế
- Phương pháp loại bỏ
- Phương pháp nhân chéo