Hướng dẫn cách chia phân số chuẩn không cần chỉnh

Một phân số thường được viết thành hai phần, trong đó tử số được hiển thị phía trên một dòng hoặc trước một dấu gạch chéo trong khi, mẫu số được hiển thị bên dưới hoặc trước dòng.

Làm thế nào để chia phân số?

Trong bài này, chúng ta sẽ tìm hiểu cách thực hiện phép chia các phân số. Có hai phương pháp chia phân số. Chúng ta hãy xem từng cái một bên dưới.

Nhân với đối ứng

Trong phương pháp này, phân số thứ hai được đảo ngược theo cách sao cho tử số trở thành mẫu số và mẫu số trở thành tử số của phân số.

Nhân phân số đầu tiên với phân số nghịch đảo và đơn giản hóa kết quả nếu có thể. Ví dụ,

1/ 2 ÷  1/ 6

• Turn ngược phân số thứ hai hoặc tìm nghịch đảo của nó:

1/6 = 6/1

• Nhân phân số thứ nhất với nghịch đảo của phân số thứ hai:

1/ 2  ×  6/ 1 = 6/2

• Đơn giản hóa phân số t thành các số hạng thấp nhất của nó:

6/2 = 3

ví dụ 1

3/8 ÷ 5/11
Viết lại phương trình và đơn giản hóa,

3/8 x 11/5 = 33/40

Ví dụ 2

2/9 ÷ 7/10

Viết lại phương trình và đơn giản hóa,

2/9 x 10/7 = 20/63

Ví dụ 3

6 ÷ 2/7

Viết lại phân số,

6/1 x 7/2 = 42/2

Đơn giản hóa phân số

42/2 = 21

Ví dụ 4

9/4 ÷ 5

Viết lại phân số và đơn giản hóa,

9/4 x 1/5 = 9/20

E xample 5

3/4 ÷ 2/5

Viết lại phân số bằng cách đổi dấu chia thành phép nhân.

3/4 ÷ 2/5 = 3/4 x 5/2 = 15/8

Ví dụ 6
2/9 ÷ 4/15

Viết lại phân số và đơn giản hóa,

2/9 ÷ 4/15 = 2/9 x 15/4 = 30/36

Đơn giản hóa phân số

30/36 = 5/6

Chia các phân số với các mẫu số khác nhau

Phương pháp này thực sự hiệu quả, nhưng nó yêu cầu bạn đổi các phân số thành các mẫu số chung trước khi bắt đầu giải.

Tuy nhiên, phương pháp chia phân số đầu tiên không yêu cầu mẫu số chung, bạn chỉ cần đảo hoặc lật phân số thứ hai và chuyển bài toán thành phép nhân.
Lấy mẫu số chung rồi chia tử số.

Xem thêm:

Công thức chuyển đổi phân số đơn giản nhất hiện nay

Người có đi có lại – Định nghĩa & Ví dụ đơn giản nhất 2021

Ví dụ 7

2/3 ÷ 1/2
Viết lại các với các mẫu số chung. Trong trường hợp này, 6 là mẫu số chung.
2/3 = 4/6
1/2 = 3/6
Chia các tử số để được kết quả cuối cùng

4/6 ÷ 3/6 = 4 ÷ 3 = 4/3

Ví dụ 8

3/8 ÷ 2/10

Viết lại các phân số có bội chung nhỏ nhất làm mẫu số của chúng.

LCM của 8 và 10 là 40

3/8 = 15/40

2/10 = 8/40
Chia tử số của các phân số

15/40 ÷ 8/40 = 15 ÷ 8 = 1 ⁷ / ₈

Thực hành câu hỏi với giải pháp

1. Chia 3/5 cho 12

Giải pháp

3/5 ÷ 12

Xác định nghịch đảo của số nguyên và nhân với phân số.

= 3/5 ÷ 12/1

= 3/5 × 1/12

= (3 × 1) / (5 × 12)

Thể hiện kết quả trong điều kiện thấp nhất của nó.

= 3/60

= 1/20

2. Tập luyện: 5/7 ÷ 10

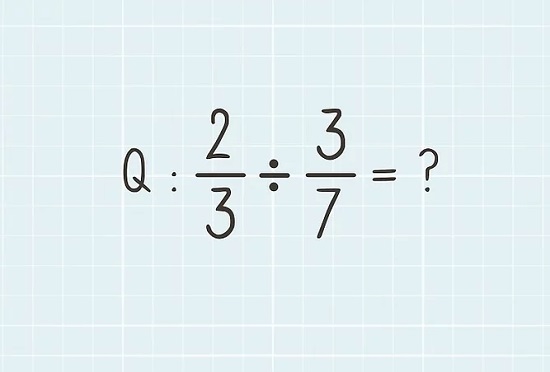
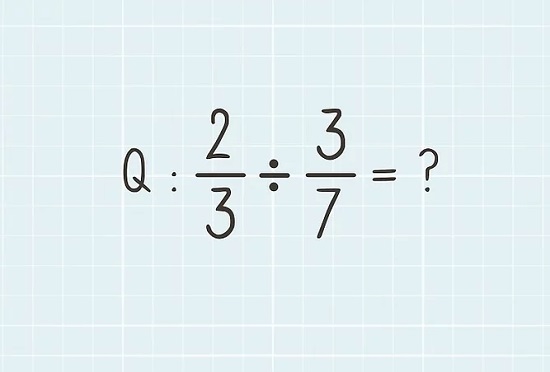
Giải pháp

Tìm nghịch đảo của số nguyên và nhân với phân số.

= 5/7 ÷ 10/1

= 5/7 × 1/10

= (5 × 1) / (7 × 10)

= 5/70

Giảm sản phẩm ở mức thấp nhất.

= 1/14

3. Chia hai phân số sau: 7/8 cho 1/5

Giải pháp

7/8 ÷ 1/5

Xác định nghịch đảo của 1/5 quảng cáo nhân nó với phân số đầu tiên

= 7/8 × 5/1

= (7 × 5) / (8 × 1)

= 35/8

Đơn giản hóa hoặc chuyển đổi sản phẩm thành một phần hỗn hợp

= 4 ³ / ₈

4. Chia: 5/9 ÷ 10/18

Giải pháp

= 5/9 × 18/10

= (5 × 18) / (9 × 10)

= 90/90

= 1

5. Giải quyết: 2 ¾ ÷ 1 ²/ ₃

Giải pháp

= 11/4 ÷ 5/3

= 11/4 × 3/5

= (11 × 3) / (4 × 5)

= 33/20

= 1 ¹³ / ₂₀

6. Divide: 2 ⁴/ ₁₇÷ 1 ⁴ / ₁₇

Giải pháp

= 38/17 ÷ 21/17

= 38/17 × 17/21

= (38 × 17) / (17 × 21)

= 646/357

= 38/21

= 1 ¹⁷ / ₂₁

7. Tập ra: 2/3 ÷ 1/3

Giải pháp

= 2/3 / 1/3

= 2/3 × 3/1

= 2/3 × 3

= 6/3

= 2

8. Chia: 1/3 ÷ 2/5

Giải pháp

Nhân phân số thứ nhất với nghịch đảo của phân số thứ hai
= 1/3 × 5/2
= (1 × 5) / (3 × 2)
= 5/6

9. Chia phần: 2 ¹/ ₇÷ 7/2

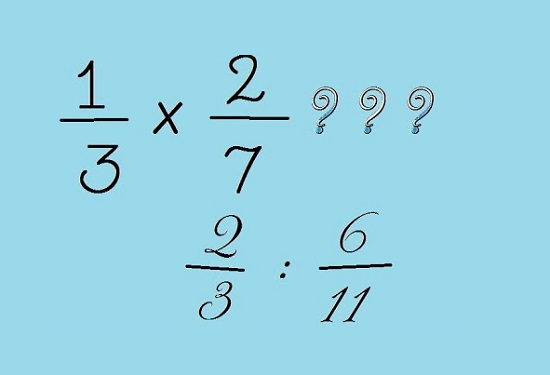
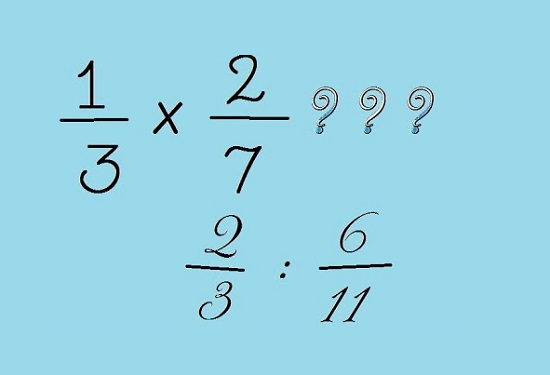
Giải pháp

= (2 × 7 + 1) / 7 ÷ 7/2
= 15/7 ÷ 7/2
= 15/7 × 2/7
= (15 × 2) / (7 × 7)
= 30/49

10. Workout: 6 ²/ ₃÷ 4 ¹ / ₅

Giải pháp

= (6 × 3 + 2) / 3 ÷ (4 × 5 + 1) / 5
= 20/3 ÷ 21/5
= 20/3 × 5/21
= (20 × 5) / (3 × 21)
= 100 / 63

11. Giải quyết: 5 ¹/ ₈÷ 8 ² / ₁₆

Giải pháp

= (5 × 8 + 1) / 8 ÷ (8 × 16 + 2) / 16
= 41/8 ÷ 130/16
= 41/8 × 16/130

= 41/65