ĐƯỜNG TRUNG TUYẾN LÀ GÌ? CÔNG THỨC ĐƯỜNG TRUNG TUYẾN

Bạn đang tìm hiểu những thông tin liên quan đến công thức đường trung tuyến những câu hỏi đặt ra đường trung tuyến là gì và cách tính đường trung tuyến như thế nào???

Để giải quyết thắc mắc trên hôm nay tintuctuyensinh của chúng tôi sẽ giúp bạn hiểu rõ khái niệm thế nào là đường trung tuyến và các dạng bài toán liên quan đến đường trung tuyến nói chung và đường trung tuyến của tam giác nói riêng.

Trên cơ sở tổng quát giúp bạn hệ thống lại lý thiết công thức đường trung tuyến và các cách tính độ dài đường trung tuyến để bạn giải quyết tốt các bài tập về đường trung và dành điểm o2r phần này.

1. NHẬN THỨC CHUNG VỀ ĐƯỜNG TRUNG TUYẾN

Trong chương trình môn Toán ở trung học cơ sở trong phần Hình học đã giới thiệu về khái niệm đường trung tuyến và các cách tính độ dài đường trung tuyến của tam giác.

Trên cơ sở đó khi nhắc đến khái niệm đường trung tuyến là gì thì chắc hẳn nhiều người biết đến nhưng để có thể giải quyết hiệu quả các bài tập liên quan đến đường trung tuyến thì lại không dễ dàng.

Chính vì vậy đầu tiên bạn cần phải nắm vững phần lý  thuyết thế nào là đường trung tuyến và các tính chất của nó.

Đường trung tuyến là gì ???

Khái niệm trong toán học đường trung tuyến của một đoạn thẳng được định nghĩa là một đường thẳng đi qua trung điểm của đoạn thẳng cho cho trước chia đoạn thẳng đó thành hai phần bằng nhau.

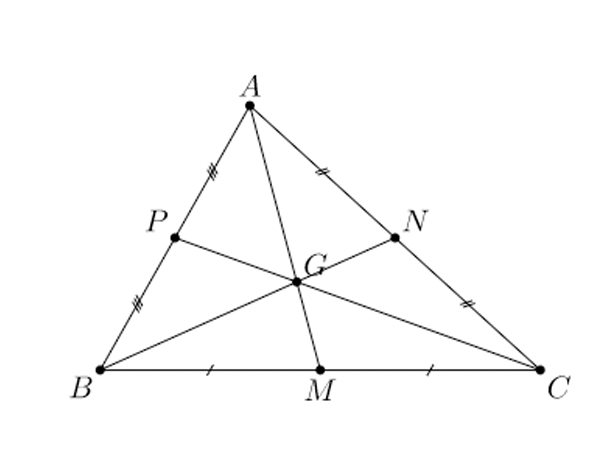
Định nghĩa đường trung tuyến của tam giác là gì???

Trong hình học phẳng khái niệm đường trung tuyến của một tam giác là đoạn thẳng hạ từ đỉnh tam giác tới cạnh đối diện và đi qua trung điểm của cạnh đó

Trong một tam giác có nhiều nhất 3 đường trung tuyến xuất phát từ ba đỉnh.

2. CÁC TÍNH CHẤT VÀ CÔNG THỨC ĐƯỜNG TRUNG TUYẾN LIÊN QUAN

Các công thức đường trung tuyến, tính chất của đường trung tuyến trong tam giác

• Trong một tam giác giao điểm của ba đường trung tuyến của tam giác gọi là trọng tâm của tam giác đó. 
• Trọng tâm của tam giác đó cách đỉnh một khoảng bằng hai phần ba độ dài đường trung tuyến đi qua đỉnh ấy.

Ví dụ:

Gọi H là trọng tâm của tam giác ABC, trong đó có các trung tuyến lần lượt là AI, BM, CN thì ta sẽ có biểu thức thể hiện tính chất của công thức đường trung tuyến đường trung tuyến là:

AH/AI = BH/BM = CH/CN = 2/3

Đường trung tuyến trong tam giác vuông

Như ta đã biết tam giác vuông là một trường hợp đặc biệt của tam giác, trong đó, có một góc có độ lớn là 90 độ do hai cạnh tạo nên và cạnh đối diện với góc vuông gọi là cạnh huyền của tam giác vuông. 

Do đó, đường trung tuyến trong tam giác vuông sẽ có đầy đủ các tính chất như một đường trung tuyến tam giác.

Các định lý về đường trung tuyến của tam giác vuông

Định lý 1: Trong một tam giác vuông, đường trung tuyến của cạnh huyền có độ dài bằng một nửa cạnh huyền.

Định lý 2: Trong một tam giác đường trung tuyến ứng với một cạnh có độ dài bằng một nửa cạnh đó thì tam giác ấy là tam giác vuông.

Ví dụ:

Trong tam giác ABC vuông ở A, ta có độ dài đường trung tuyến AI sẽ chia cạnh BC bằng hai đoạn bằng nhau IB, IC và độ dài bằng một nửa cạnh BC

Ngược lại nếu AI có độ dài bằng một nửa cạnh BC thì tam giác ABC vuông ở A.

3. CÁC BÀI TẬP LIÊN QUAN CÔNG THỨC ĐƯỜNG TRUNG TUYẾN

Bài tập công thức đường trung tuyến 1: Cho tam giác ABC cân ở A có AB = AC = 10cm, BC= 14cm. Kẻ trung tuyến AI.

a) Chứng minh: AI ⊥ BC;

b) Tính độ dài đường trung AI.

Giải

Ta có đường thẳng AI là đường trung tuyến của tam giác ABC nên IB = IC

Mặt khác tam giác ABC là tam giác cân tại A

Nên AI vừa là đường trung tuyến vừa là đường cao

Vậy AI vuông góc với BC (điều phải chứng minh)

Ta có

BC = 14cm nên BI= CI= 7cm

AB = AC = 10cm

Xét tam giác AIC vuông tại I

Áp dụng định lý Pitago ta có:

AI2 = AC2 + IC2 => AI = √149 cm

Bài tập công thức đường trung tuyến 2:  Cho tam giác đều ABC. Điểm I là trọng tâm của tam giác đều ABC. Chứng minh rằng IA = IB = IC.

Giải

Gọi AD, CE, BF là các đường trung tuyến tam giác ABC hay D, E, F lần lượt là trung điểm của các cạnh BC, AB, AC

Khi đó ta có AD là đường trung tuyến của cạnh BC 

CE là đường trung tuyến tam giác AB 

BF là đường trung tuyến tam giác AC 

Bên cạnh đó tam giác ABC đều nên suy ra AD = BF = CE 

Từ các giả thiết ở trên ta suy ra AI = BI = CI (điều phải chứng minh)

Như vậy qua các bài tập hướng dẫn ở trên chúng ta có thể thấy kiến thức và các dạng gián liên quan đến công thức đường trung tuyến không quá khó nhưng nếu bạn không nắm vững được lý thuyết về đường trung tuyến thì sẽ rất khó để giải quyết được.

Trên đây là toàn bộ những kiến thức liên quan đến đường trung tuyến mà tintuctuyensinh của chúng tôi cung cấp cho các bạn tham khảo.

Hy vọng công thức đường trung tuyến trên đây là tài liệu bổ ích giúp các bạn nâng cao hiểu biết về các tính chất của đường trung tuyến và cách giải quyết hiệu quả các bài tập liên quan đến công thức đường trung tuyến này.

Từ đó xây dựng và lựa chọn cho mình phương pháp học tập khoa học và tốt nhất để bạn dành được kết quả học tập cao nhất qua các kì thi. Chúc các bạn sức khỏe và thành công!!!

Xem thêm: 

Số phủ định – Một số kiến thức bổ ích liên quan đến nó

Kỳ thi tốt nghiệp THPT năm 2021: Từ khóa là “ổn định”

Hướng dẫn giải phân số phức tạp nhanh chóng nhất