CÔNG THỨC HERON VÀ CÁCH SỬ DỤNG ĐƠN GIẢN NHẤT

Công thức Heron là gì?

Dùng để làm gì?

Áp dụng như thế nào

      Bạn đang tìm kiếm các công thức có liên quan đến tính diện tích tam giác. Bạn không biết cách sử dụng và chưa rõ tại sao lại có công thức như vậy.

Hôm nay, kênh tintuctuyensinh sẽ gửi đến các bạn câu trả lời giải đáp hết các thắc mắc trên. 

1, Công thức Heron:

Heron là công thức gì?

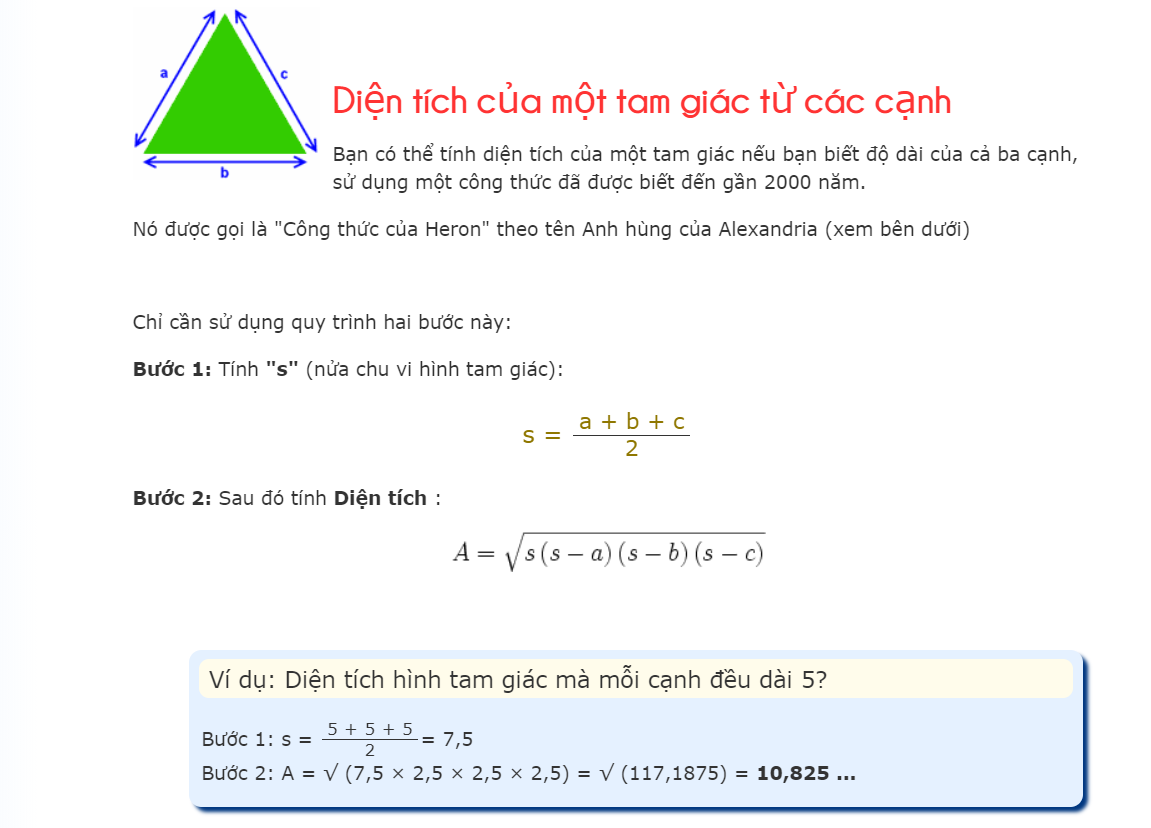
        Công thức Heron là công thức toán học được lấy tên theo nhà Toán học vĩ đại Heron. Trong hình học phẳng, công thức Heron là công thức dùng để tính diện tích của một tam giác có độ dài 3 cạnh đã biết. 

Ví dụ 1: Cho tam giác ABC, có độ dài cạnh AB =2, BC =3, AC =4. Tính diện tích tam giác ABC?

Ví dụ 2: Cho tam giác BCD, các cạnh BC,CD,BD có độ dài tương ứng lần lượt là 3,4,5. Tính diện tích tam giác BCD?

         Công thức Heron là một trong những công thức tính diện tích tam giác được sử dụng khá phổ biến ở các bạn học sinh cấp hai. Tuy nhiên, do mức độ áp dụng còn hạn chế nên công thức Heron chỉ áp dụng trong một số trường hợp khi và chỉ khi tìm kiếm được độ dài số đo của tất cả các cạnh của tam giác hay được áp dụng để tìm cạnh của một tam giác khi biết diện tích và 2 cạnh còn lại.  

Công thức Heron?

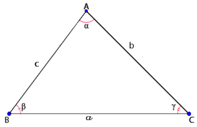
Đặt S là diện tích tam giác ABC như trong hình vẽ, có độ dài các cặp cạnh tương ứng là a,b,c.    

Ta có: Công thức heron:

Theo hình ta có:

          S = √p (p – a)(p – b)(p – c)

Trong đó: 

         p là nửa chu vi tam giác p= ( a + b + c)/2

Ngoài công thức Heron trên thì nó còn được biến đổi thành các dạng khác như:

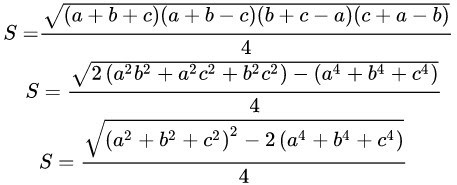
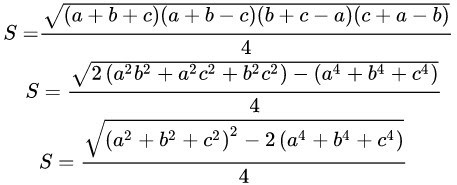
        Do có sự biến đổi về công thức, nên khi sử dụng công thức Heron, các bạn cần chú ý đến các dữ kiện mà mình đã có để xác định công thức cần thiết để áp dụng. Tùy vào khả năng của mỗi người, họ sẽ chọn một trong bốn công thức dễ dàng với mình hơn để thực hiện. Tuy nhiên, phần lớn các bạn lựa chọn công thức đầu không có sự biến đổi vì nó khá đơn giản hơn các công thức biến đổi sau này.

2, Vì sao có công thức Heron như thế này?

Chứng minh công thức Heron:

Ta có theo hệ quả Cosin:

(1)

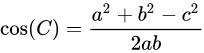
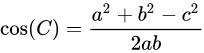
(2)

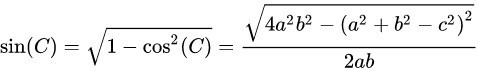
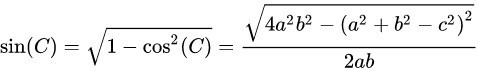
       Theo công thức diện tích tam giác, diện tích tam giác bằng một phần hai đường cao nhân cạnh đáy tương ứng, dựa theo (1) và (2) ta có:

3, Áp dụng vào bài tập:

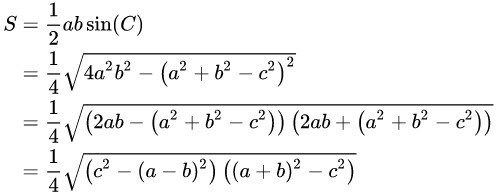
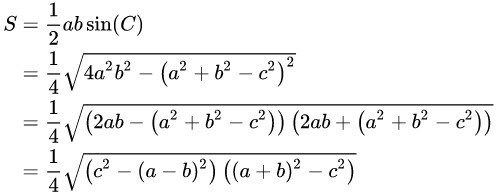
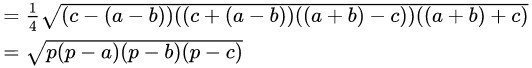
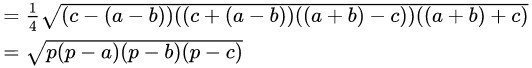
Bước 1: Tìm độ dài tất cả các cạnh của tam giác theo đề bài yêu cầu.

Bước 2: Tính nữa chu vi tam giác theo độ dài các cạnh đã tìm được.

Bước 3: Áp dụng công thức Heron vào giải bài toán.

        Rất đơn giản, chỉ với 3 bước mà các bạn đã thực hiện xong một bài toán tính diện tích tam giác. Tuy nhiên, vẫn luôn có sự biến đổi trong cách ra đề như lồng ghép thêm các dữ kiện gây khó khăn hơn trong việc tính các cạnh của tam giác. Khó khăn nhất trong bài toán tìm diện tích tam giác bằng công thức Heron là bước thứ nhất, tìm độ dài các cạnh tam giác. Vì đây là bước rất quan trọng và thiết yếu nhất. Quyết định áp dụng được hay không công thức Heron, nên khi ra đề độ khó thường tập trung vào bước này.

Bài tập:

Bài 1: Cho tam giác ABC có AB = 3, BC = 4, AC = 3. Tính diện tích tam giác ABC?

                                 Bài giải

Gọi S là diện tích tam giác ABC.

       p là nửa chu vi tam giác ABC.

Ta có: 

p= (3+4+3)/2 = 5.

Áp dụng công thức Heron ta có: 

S= √5(5-3)(5-4)(5-3) =√20 đvdt.

Vậy diện tích tam giác ABC là S= √20 đvdt.

Bài 2: Cho tam giác ABC có tọa độ 3 đỉnh A(1;-1), B(4;-3), C(0;0). Tính diện tích tam giác ABC.

                               Bài giải

Ta có:

AB =√(4-1)²+(-3+1)² = √13

BC= 5

AC =√2

Nửa chu vi p= (√13 + 5 + √2)/2 = 5,1

Ta có :

S= √ 5,1(5,1-√13)(5,1-5)(5,1-√2)= 1,68 đvdt.

Vậy diện tích tam giác ABC là S= 1,68 đvdt.

         Lời khuyên cho các bạn, do mức độ phức tạp của công thức, nên khi thực hiện thao tác tính toán. Các bạn có thể thực hiện nhanh bằng cách tính nhẩm đối với các bạn có khả năng tính nhanh. Ngược lại, các bạn nên sử dụng máy tính cầm tay hoặc ghi ra giấy để thực hiện phép tính cho chính xác. Sự phức tạp trong các phép tính dễ gây nhầm lẫn dẫn đến kết quả sai thì thật đáng tiếc cho các bạn.

Phía trên là những kiến thức mà kênh tintuctuyensinh gửi đến các bạn, những người đang tìm kiếm về công thức Heron. Hi vọng chúng giúp ích cho các bạn. Chúc các bạn thành công!

CÔNG THỨC HERON DƯỚI ĐÂY CÁC BẠN XEM THÊM NẾU KHÔNG HIỂU BÊN TRÊN

Xem thêm:

So sánh số thứ tự thường gặp nhất hiện nay

Quy tắc chia hết – Phương pháp & Ví dụ thường gặp

Ký hiệu mở rộng – Cách để mở rộng số dễ hiểu nhất