Góc nhìn tổng quan về công thức hình trụ

Bạn đang tìm hiểu những thông tin liên quan đến hình trụ và các công thức hình trụ như thế nào, công thức tính diện tích hình trụ như sao… Đây là hàng loạt các câu hỏi xoay quanh khái niệm hình và các công thức hình trụ.

Để giải đáp những thắc mắc trên hôm nay tintuctuyensinh của chúng tôi sẽ giúp bạn có một cái nhìn khái quát về khái niệm hình trụ và các công thức hình trụ. Từ đó giúp bạn hiểu rõ được hệ thống lý thuyết từ cơ bản đến nâng cao trong hình học không gian của phần kiến thức trung học phổ thông. Giúp bạn có thể dễ dàng nắm được những nội dung bài học quan trọng về hình trụ và các giải quyết các dạng, loại bài tập mà bạn thường gặp phải trong phần kiến thức mình theo học và đáp ứng cho kỳ thi trung học phổ thông quốc gia.

1. Nhận thức thức về hình trụ 

Trong toán học hình học là một trong những bộ phận không thể thiếu tạo nên sự đa dạng và hứng thú cho môn học này. Đây là môn khoa học về hình học không gian giúp cho con người có những cái nhìn đa chiều về không gian những hình dạng trong cuộc sống mà chúng ta thường bắt gặp cũng như nhận biết được các vật thể có các hình dạng khác nhau. 

Đồng thời toán học còn giúp chúng ta tính toán được các diện tích thể tích kích thước của các vật thể có hình dạng đặc biệt. Từ đó tạo điều kiện thuận lợi cho chúng ta sử dụng cũng như ứng dụng hiệu quả trong cuộc sống như xây dựng trang trí nghệ thuật, mỹ thuật …

Chúng ta có thể kể đến các dạng hình học đặc biệt mà chúng ta thường nhắc đến và đã được học như hình tròn, hình vuông, hình tam giác, hình lục giác, tứ giác…

Một trong số đó không thể không kể đến đó là hình trụ.

Trong đời sống hàng ngày chúng ta có thể dễ dàng bắt gặp vô số đồ vật, vật dụng có dạng hình trụ như: cột nhà, chai nước, ống nước, cây sáo…. 

Vậy câu hỏi đặt ra: Khái niệm hình trụ theo phương diện toán học là gì???

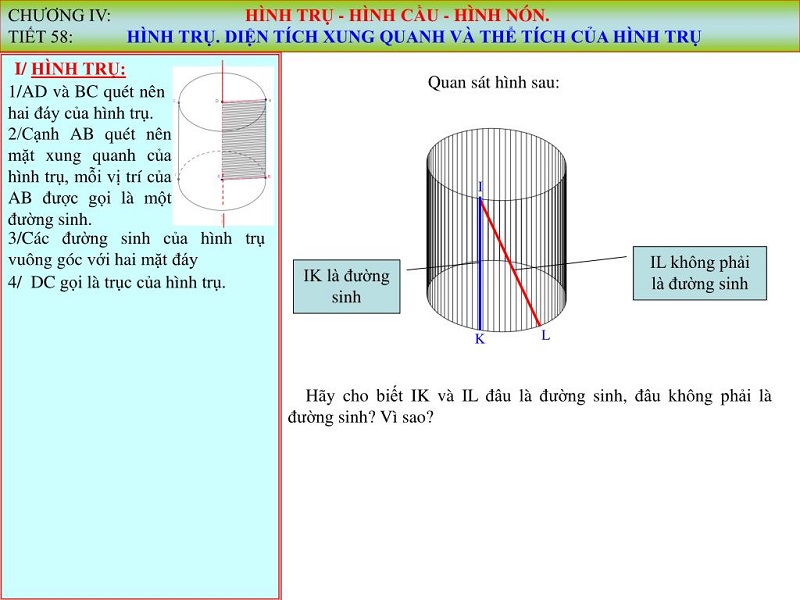
Theo những nghiên cứu và đánh giá đúc rút từ nhiều nhà khoa học về toán học từ xưa đến này đã đưa ra khái niệm về hình trụ như sau: Hình trụ là hình được giới hạn bởi hai đường tròn có đường kính bằng nhau và mặt trụ bao quanh hai đáy.

Hay khi quay hình chữ nhật quay một trục cố định theo một vòng tròn thì ta được hình trụ với hai đáy có bán kính là độ dài hai cạnh nhỏ của hình chữ nhật và chiều cao của hình trụ là độ dài đường sinh.         

Trong đó  h là chiều cao của hình trụ và r là bán kính của 2 dáy trên và dưới của hình trụ

2. Các công thức hình trụ

•  Công thức tính diện tích hình trụ

Hình trụ là hình có 2 đáy là 2 hình tròn bằng nhau và nằm song song với nhau. Từ những bài đơn giản đến phức tạp trong các bài toán liên quan đến Hình trụ được sử dụng khá phổ biến. Trong đó liên quan đến công thức hình trụ, thể tích hình trụ thường được sử dụng khá nhiều và chủ yếu trong các bài toán hình học không gian.

 Nếu bạn đã biết cách tính diện tích và chu vi thể tích của hình tròn thì đó là cơ sở quan trọng để bạn có thể dễ dàng suy luận ra các công thức tính thể tích, diện tích xung quanh cũng như diện tích toàn phần của hình trụ.               

Diện tích hình trụ bao gồm diện tích xung quanh và diện tích toàn phần.

Diện tích xung quanh của hình trụ là diện tích của bề mặt xung quanh của hình trụ mà không bao gồm diện tích của hai đáy.

Diện tích toàn phần của hình trụ là phần diện tích xung quanh không gian bao quanh bên trong và phần diện tích của hai đáy.

Công thức tính diện tích xung quanh của hình trụ bằng chu vi đường tròn đáy nhân với chiều cao của hình trụ

 Sxq = 2πrh

Trong đó r là bán kính của đáy

h là chiều cao của hình trụ nối từ đáy tới đỉnh hình trụ

Công thức tính diện tích toàn phần của hình trụ bằng diện tích xung quanh cộng với diện tích của hai đáy

S tp = 2πrh + 2πr 2

Trong đó r là bán kính của đáy

h là chiều cao của hình trụ nối từ tâm của hai đáy

• Công thức tính thể tích của hình trụ

Thể tích của hình trụ là phần không gian  bên trong mà hình trụ chiếm được. Hay là phần thể tích mà hình trụ chứa được ở bên trong.

Thể tích của hình trụ bằng diện tích của mặt đáy nhân với chiều cao.

Công thức tính thể tích như sau:

V = πr 2 giờ

Trong đó r là bán kính của đáy hình trụ

h là chiều cao của hình trụ nối từ tâm của hai đáy.

Như vậy các công thức liên quan đến hình trụ tuy rất ngắn và đơn giản nhưng chúng lại không dễ dàng để nhớ bởi vậy cách để nhớ lâu nhất đó là bạn phải thực hành làm các bài tập liên quan đến công thức này và nắm được bản chất của các công thức để cơ thể nhớ lâu hơn, từ đó giải quyết hiệu quả các bài toán liên quan đến hình trụ và các công thức liên quan.

Trên đây là toàn bộ những thông tin liên quan đến công thức hình trụ mà tintuctuyensinh của chúng tôi cung cấp cho các bạn tham khảo.

Xem thêm bài viết:

Hướng dẫn cách trừ các số hỗn hợp chưa đầy 1 phút

Phương pháp và ví dụ trừ các phân số nhanh chóng nhất

Phân số tương đương và những cách giải nhanh chóng nhất