Công thức lượng giác cơ bản mà bạn cần ghi nhớ

Lượng giác là một chủ đề toán học tương đối khó so với một số bạn học sinh. Bởi vì lượng giác là các công thức buộc chúng ta phải nhớ công thức lượng giác cơ bản, chúng rất có ích trong giải toán.

        Hiểu được sự khó khăn của các bạn, hôm nay kênh tintuctuyensinh sẽ gửi đến các bạn những công thức lượng giác cơ bản tạo tiền đề cho các công thức lượng giác nâng cao sau này.

Công thức lượng giác là gì?

        Công thức lượng giác là các công thức mà các bạn bắt buộc phải học thuộc lòng, bởi vì khi mà các bạn thuộc được công thức thì mới giải quyết đc bài toán.

        Muốn học được lượng giác, chúng ta cần phải biết đến giá trị lượng giác của các cung, góc đặc biệt.

Tương ứng với sinx, cosx, tanx, cotx thì các góc 0°,30°,45°,60°,90° có những giá trị lượng giác khác nhau. Nhưng chúng sẽ có sự phân bố có quy luật cân xứng nhau trong các giá trị trên.

        Vì sao có các giá trị trên, để giải thích chúng ta hãy nghiên cứu đường tròn lượng giác với các góc tương ứng.

1, Các công thức lượng giác cơ bản cần phải biết:

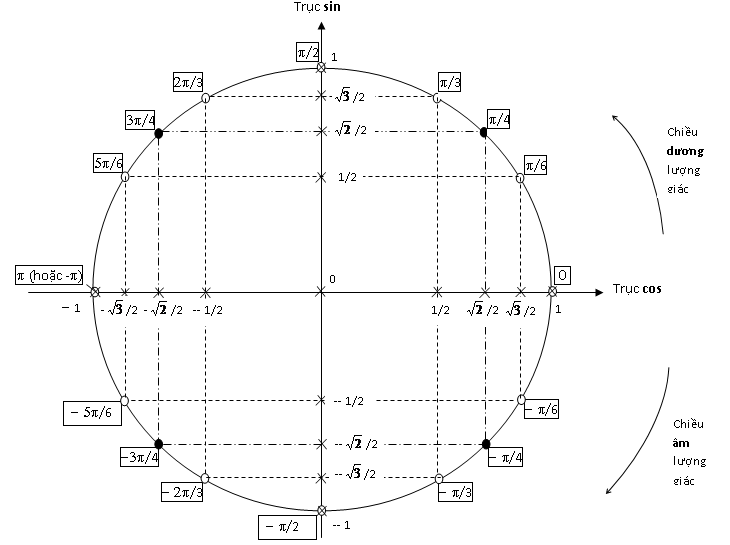
Ta có:

Sin²x + Cos²x = 1

Tanx.Cotx = 1, x khác k.π/2, k€ Z

1 + tan²x = 1/cos²x , x khác π/2 + kπ, k€ Z

1 + Cot²x = 1/sin²x, x khác k.π, k€ Z

Tanx = Sinx/ Cosx

Cotx = Cosx/Sinx

Mối liên hệ giữa các góc: cos đối, sin bù, phụ chéo, tan kém bi.

Có nghĩa là:

• Hai góc đối nhau

cos(–x) = cosx

sin(–x) = – sinx

tan(–x) = – tanx

cot(–x) = – cotx

• Hai góc bù nhau

sin (π – x) = sinx

cos (π – x) = -cosx

tan (π – x) =  -tanx

cot (π – x) = -cotx

• Hai góc hơn kém π

sin (π + x) = -sinx

cos (π + x) = -cosx

tan (π + x) = tanx

cot (π + x) = cotx

• Hai góc phụ nhau

Sin (π/2 – x) = cosx

Cos (π/2 – x) = sinx

Tan (π/2 – x) = cotx

Cot (π/2 – x) = tanx

• Hai góc hơn kém π/2

Sin (π/2 + x) = cosx

Cos (π/2 + x) = – Sinx

Tan (π/2 + x) = – cotx

Cot (π/2 + x) = – tanx.

2, Công thức lượng giác cơ bản nhân đôi trong lượng giác:

Cos2x = cos²x – sin²x

           = 2cos²x – 1

           = 1 – 2sin²x

Sin2x = 2sinx.cosx

Tan 2x = 2tanx/ ( 1- tan²x)

Cot2x = (1- cot²x)/ 2cotx

3, Công thức lượng giác cơ bản nhân 3:

cos3x = 4cos3x – 3cosx

sin3x = 3sinx – 4sin3x

4, Công thức lượng giác cơ bản cộng:

Sin (a + b) = sina.cosb + cosa.sinb

Sin (a – b) = sina.cosb – cosa.sinb

Cos (a+b) = cosa.cosb – sina.sinb

Cos (a-b) = cosa.cosb + sina.sinb

Tan (a+b) = (tana + tanb)/(1 – tana.tanb)

Tan (a-b) = (tana – tanb)/(1 + tana.tanb)

5, Công thức lượng giác cơ bản hạ bậc:

Sin²x= ½(1-cos2x)

Cos²x=½(1+cos2x)

Sin³x=¼(3sinx-sin3x)

Cos³x=¼(3cosx+cos3x)

Tan²x=(1-cos2x)/(1+cos2x)

6, Công thức lượng giác cơ bản tổng hiệu sin cos:

Sinx +cosx =√2.sin (x + π/4)= √2.cos (x – π/4)

Sinx -cosx =√2.sin (x – π/4)= √2.cos (x + π/4)

7, Công thức lượng giác cơ bản chia đôi:

         Đặt t= tan(x/2)

Sinx= 2t/(1+t²)

Cosx= (1+ t²)/(1 – t²)

Tanx= 2t/(1 – t²)

8, Công thức lượng giác cơ bản biến đổi tích thành tổng:

Cosx.cosy= ½[cos(x+y)+cos(x-y)]

Sinx.siny= – ½[cos(x+y) – cos(x-y)]

              = ½ [cos(x-y) – cos(x+y)]

Sinx.cosy= ½[sin(x+y)+ sin (x-y)]

        Công thức lượng giác rất phức tạp và tương đối khó nhớ trong quá trình làm bài. Nhưng mức độ quan trọng của chúng rất cao. Nếu không áp dụng được các công thức này thì một số bài toán các bạn không thể giải được.

Ví dụ: Tính các giá trị lượng giác của các góc số đo như sau:

a.15° 

1. 2π/5

c.75°

1. 3π/4

Cách làm:

Ta có: Phân tích 15o = 60° – 45° hoặc 45° – 30° rồi sử dụng các công thức cộng.

Tương tự, ta phân tách các góc trên thành các góc dưới dạng các góc đặc biệt tổng hoặc hiệu để tính.

Sự phát triển của máy tính cầm tay chính là sự giúp đỡ rất lớn cho các bạn trong việc thực hiện các phép tính về lượng giác. 

Có sự giúp đỡ của máy tính cầm tay, các công thức lượng giác được thực hiện một cách dễ dàng hơn. 

Các giá trị lượng giác sin hoặc cos sẽ được tính nhanh và có hiệu quả hơn việc thông qua đường tròn lượng giác. Việc đó tốn rất nhiều thời gian của các bạn.

Việc thực hiện phép tính lượng giác có sự biến đổi rất nhiều trong công thức. Từ tổng sang tích, từ tích sang tổng hay chuyển sang tổng hoặc hiệu các giá trị lượng giác rất dễ bị nhầm lẫn giữa các Công thức lượng giác cơ bản. 

Vì vậy, việc thực hiện phép tính lượng giác cần phải cẩn thận thực hiện. Tốt nhất các bạn nên thuộc lòng các công thức này vì việc học thuộc lòng giúp đảm bảo độ chính xác và tiết kiệm thời gian rất nhiều cho các bạn.

Cuối cùng, kênh tintuctuyensinh hy vọng những kiến thức công thức lượng giác cơ bản trên sẽ giúp ích cho các bạn trong việc giải toán về lượng giác. 

Những kiến thức kèm theo hướng dẫn về lượng giác sẽ giúp các bạn định hình được như thế nào về Công thức lượng giác cơ bản. Các bạn có thể tham khảo thêm các công thức lượng giác mở rộng và nâng cao để giúp khả năng giải toán của mình được tốt hơn. 

Xin chúc các bạn mai mắn!

Xem thêm:

So sánh số thứ tự thường gặp nhất hiện nay

Quy tắc chia hết – Phương pháp & Ví dụ thường gặp

Ký hiệu mở rộng – Cách để mở rộng số dễ hiểu nhất