Bổ sung – Những kiến thức cơ bản bạn cần biết
7 Tháng Ba, 2021Contents Bổ sung – Giải thích & Ví dụ Phép cộng là một trong những phép toán số học...
Phép chia là một trong bốn phép toán cơ bản phân phối một số thành các phần bằng nhau. Nó được định nghĩa là một kỹ thuật toán học trong đó một số được chia sẻ thành các nhóm nhỏ hơn hoặc kỹ thuật phân phối các đại lượng thành các phần bằng nhau. Nó được biểu thị bằng một số ký hiệu bao gồm, dấu gạch chéo, đường ngang và dấu phân chia.
Phép chia là một phép toán nghịch đảo của phép nhân. Ví dụ, phép nhân 5 với 2 cho 10. Một trong hai thừa số 2 và 5 có thể nhận được bằng cách chia 10 cho bất kỳ số nào.
Contents
Quy tắc chia hết đã được phát triển để làm cho quá trình phân chia dễ dàng và nhanh chóng hơn . Hiểu các quy tắc chia hết cho 1 đến 20 là một kỹ năng quan trọng trong toán học vì nó cho phép bạn giải quyết vấn đề theo cách tốt hơn.
Ví dụ, quy tắc chia hết cho số 9 chắc chắn sẽ cho chúng ta biết liệu số đó có chia hết cho 9 hay không, bất kể số đó có vẻ lớn như thế nào.
Các quy tắc chia hết cho các số như 2, 3, 4 và 5 có thể được ghi nhớ một cách dễ dàng. Nhưng các quy tắc chia hết cho 7, 11 và 13 hơi phức tạp và vì lý do này, cần phải hiểu chúng một cách công phu.

Quy tắc chia hết
Như tên cho thấy, các quy tắc chia hết hoặc kiểm tra là các thủ tục được sử dụng để kiểm tra xem một số có chia hết cho một số khác mà không nhất thiết phải thực hiện phép chia thực tế hay không. Một số chia hết cho một số khác nếu kết quả hoặc thương là một số nguyên và phần dư là số không.
Vì không phải tất cả các số đều chia hết hoàn toàn cho các số khác, do đó, các quy tắc chia hết thực sự là các phím tắt để xác định ước số thực của một số chỉ bằng cách kiểm tra các chữ số tạo thành số đó.
Bây giờ chúng ta hãy xem xét các quy tắc chia hết cho các số khác nhau.
Phép thử chia hết cho 1 không có bất kỳ điều kiện nào đối với các số. Tất cả các số đều chia hết cho 1 không phân biệt số lớn như thế nào. Khi bất kỳ số nào chia cho 1, kết quả là chính số đó. Ví dụ: 5/1 = 5 và 100000/1 = 100000.
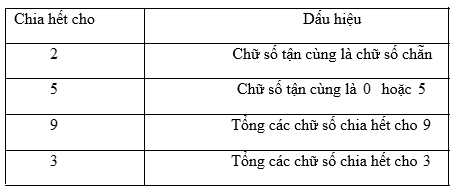
Một số chia hết cho 2 nếu chữ số tận cùng của số đó là 2, 4, 6, 8 hoặc 0.
Ví dụ: 102/2 = 51, 54/2 = 27, 66/2 = 33, 28/2 = 14 và 20/2 = 10
Phép thử tính chia hết cho 3 cho biết rằng một số hoàn toàn chia hết cho 3 nếu các chữ số của số đó chia hết cho 3 hoặc là bội của 3.
Ví dụ, hãy xem xét hai số 308 và 207:
Để kiểm tra xem 308 có chia hết cho 3 hay không, hãy tìm tổng các chữ số.
3 + 0 + 8 = 11. Vì tổng là 11 không chia hết cho 3 nên 308 cũng không chia hết cho 3.
Kiểm tra 207 bằng cách tính tổng các chữ số của nó: 2 + 0 + 7 = 9, vì 9 là bội của 3 nên 207 cũng chia hết cho 3.
Phép thử chia hết cho 4 cho biết rằng, một số chia hết cho 4 nếu hai chữ số cuối của số đó chia hết cho 4,
Ví dụ: Xét hai số, 2508 và 2506.
Các chữ số tận cùng của số 2508 là 08. Vì 08 chia hết cho 4 nên số 2508 cũng chia hết cho 4.
2506 không chia hết cho 4 vì hai chữ số tận cùng; 06 không chia hết cho 4.
Tất cả các số có chữ số tận cùng là 0 hoặc 5 đều chia hết cho 5. Ví dụ: 100/5 = 20, 205/5 = 41.


Một số chia hết cho 6 nếu chữ số tận cùng của nó là số chẵn hoặc số 0 và tổng các chữ số là bội của 3.
Ví dụ: 270 chia hết cho 2 vì chữ số tận cùng là 0.
Tổng các chữ số là: 2 + 7 + 0 = 9 cũng chia hết cho 3.
Do đó, 270 chia hết cho 6.
Kiểm tra tính chia hết của 7 được giải thích trong thuật toán sau
Xét một số 1073. Để kiểm tra số đó có chia hết cho 7 hay không?
Loại bỏ số 3 và nhân với 2, được 6. Lấy số còn lại trừ đi 6, do đó 107 – 6 = 101.
Lặp lại quá trình một lần nữa ta có 1 x 2 = 2 và số còn lại là 10 – 2 = 8. Vì 8 không chia hết cho 7 nên số 1073 cũng không chia hết cho 7.
Bài kiểm tra tính chia hết cho 8 nói rằng, một số chia hết cho 8 nếu ba chữ số cuối của nó chia hết cho 8.
Phép thử chia hết cho 9 cũng giống như phép thử chia hết cho 3. Nếu tổng các chữ số của một số chia hết cho 9 thì số đó cũng chia hết cho 9.
Ví dụ: Trong một số như 78532, tổng các chữ số của nó là: 7 + 8 + 5 + 3 + 2 = 25. Vì 25 không chia hết cho 9 nên 78532 cũng không chia hết cho 9. Xét một trường hợp khác của số: 686997, tổng các chữ số là: 6 + 8 + 6 + 9 + 9 + 7 = 45. Vì tổng chia hết cho 9 nên số 686997 chia hết cho 9.


Quy tắc chia hết cho 10 nói rằng, bất kỳ số nào có chữ số cuối cùng là 0, thì số I chia hết cho 10.
Ví dụ: Các số: 30, 50, 8000, 20 33000 chia hết cho 10.
Xem thêm:
Phép nhân là gì? Phương pháp học hiệu quả nhất
Hướng dẫn cách làm phép trừ chuẩn nhất năm 2021
Lập trình tuyến tính PDF là gì? Xem xong 5 phút hiểu luôn.
Lập trình tuyến tính cho lớp 12 là gì? Xem xong 5 phút hiểu luôn.
Sự khác biệt giữa tính chất chuyên sâu và mở rộng dễ hiểu
Quy tắc này nói rằng, một số chia hết cho 11 nếu hiệu của tổng các chữ số thay thế chia hết cho 11.
Ví dụ, để kiểm tra xem số 2143 có chia hết cho 11 hay không, quy trình là:
Tổng các chữ số thay thế của mỗi nhóm là: 2 + 4 = 6 và 1+ 3 = 4
Do đó, 6-4 = 2, và do đó số không chia hết cho 11. Do đó 2143 không chia hết cho 11.
Để kiểm tra xem một số có chia hết cho 13 hay không, thực hiện lặp lại phép cộng chữ số cuối cùng 4 lần với số còn lại cho đến khi có số có hai chữ số. Nếu số có hai chữ số chia hết cho 13 thì số nguyên đó cũng chia hết cho 13.
Ví dụ
2795 → 279 + (5 x 4) → 279 + (20) → 299 → 29 + (9 x 4) → 29 + 36 → 65.
Trong trường hợp này, số có hai chữ số là 65 chia hết cho 13, do đó, số 2795 cũng chia hết cho 13.