CÁC CÔNG THỨC NHÂN ĐÔI ĐƠN GIẢN TRONG LƯỢNG GIÁC

Công thức nhân đôi là một dạng của công thức lượng giác. Công thức nhân đôi giúp ích rất nhiều cho học sinh trong giải quyết các bài toán mà có sự thay đổi công thức so với các công thức cơ bản của lượng giác.

        Biết được các bạn đang tìm kiếm công thức nhân đôi trong lượng giác, hôm nay kênh tintuctuyensinh sẽ gửi đến các bạn những công thức về công thức nhân đôi tạo tiền đề cho các công thức lượng giác nâng cao sau này.

1, Công thức nhân đôi lượng giác là gì?

        Công thức lượng giác là các công thức mà các bạn bắt buộc phải học thuộc lòng, bởi vì khi mà các bạn thuộc được công thức thì mới giải quyết đc bài toán.

        Muốn học được lượng giác, chúng ta cần phải biết đến giá trị lượng giác của các cung, góc đặc biệt.

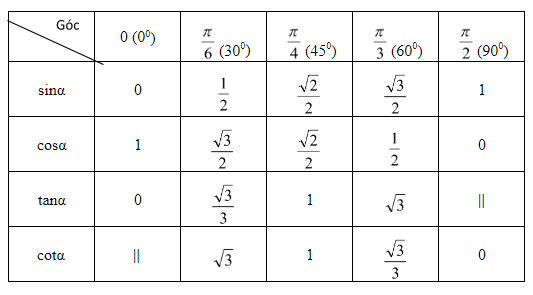
Tương ứng với sinx, cosx, tanx, cotx thì các góc 0°,30°,45°,60°,90° có những giá trị lượng giác khác nhau. Nhưng chúng sẽ có sự phân bố có quy luật cân xứng nhau trong các giá trị trên.

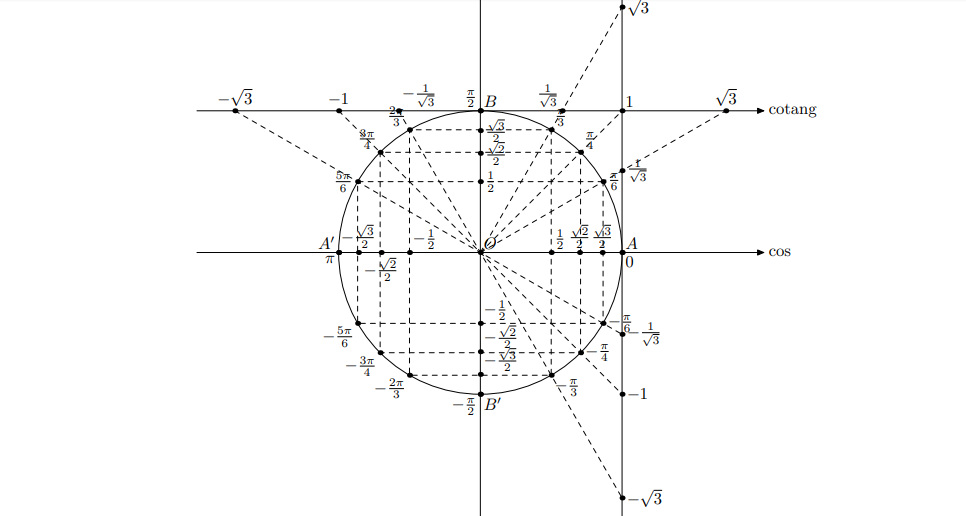
        Vì sao có các giá trị trên, để giải thích chúng ta hãy nghiên cứu đường tròn lượng giác với các góc tương ứng.

 2, Công thức nhân đôi trong lượng giác:

• Cos2x = cos²x – sin²x

           = 2cos²x – 1

           = 1 – 2sin²x

• Sin2x = 2sinx.cosx
• Tan 2x = 2tanx/ ( 1- tan²x)
• Cot2x = (1- cot²x)/ 2cotx

Để có được các công thức trên, ta cần phải dựa trên cơ sở các góc và công thức cơ bản trong lượng giác, như sau:

Công thức lượng giác cơ bản nhất:

Sin²x + Cos²x = 1

Tanx.Cotx = 1, x khác k.π/2, k€ Z

1 + tan²x = 1/cos²x , x khác π/2 + kπ, k€ Z

1 + Cot²x = 1/sin²x, x khác k.π, k€ Z

Tanx = Sinx/ Cosx

Cotx = Cosx/Sinx

Mối liên hệ giữa các góc: cos đối, sin bù, phụ chéo, tan kém bi.

Có nghĩa là:

• Hai góc đối nhau

cos(–x) = cosx

sin(–x) = – sinx

tan(–x) = – tanx

cot(–x) = – cotx

• Hai góc bù nhau

sin (π – x) = sinx

cos (π – x) = -cosx

tan (π – x) =  -tanx

cot (π – x) = -cotx

• Hai góc hơn kém π

sin (π + x) = -sinx

cos (π + x) = -cosx

tan (π + x) = tanx

cot (π + x) = cotx

• Hai góc phụ nhau

Sin (π/2 – x) = cosx

Cos (π/2 – x) = sinx

Tan (π/2 – x) = cotx

Cot (π/2 – x) = tanx

• Hai góc hơn kém π/2

Sin (π/2 + x) = cosx

Cos (π/2 + x) = – Sinx

Tan (π/2 + x) = – cotx

Cot (π/2 + x) = – tanx.

Dựa trên các công thức cơ bản, ta suy ra được công thức nhân đôi.

Chứng minh :

Vận dụng các công thức sin ( a + b ) , cos ( a +b) và tg ( a + b ) .

Cụ thể : 

sin 2a = sin ( a + a ) = sina.cosa + sina.cosa 

          = 2 sina. cosa 

cos 2a = cos ( a + a ) = cosa. cosa – sina. sina 

           = cos²a – sin²a 

tg2a = (tga + tga)/(1 – tga.tga) = 2tga/(1- tg²a)

Bài tập vận dụng:

Bài tập 1: Tính giá trị của biểu thức sau:

M = (5 – cos²x)/ (2+ 7sinx) 

Giải

M =[5-(1-sin²x)/(2+7sinx) 

    =(4 +sin²x)/(2+7sinx)

    Đặt tag ½x = ½

⇒ sinx = 2t/ (1+ t² ) = (2.½) / (1+ ¼) = ⅘

⇒ M = (4 +(⅘)²)/ (2+7.⅘)= 58/95.

Bài tập 2: Chứng minh các biểu thức sau là những hằng số không phụ thuộc vào a.

1. a) A = 2(sin²α + cos6²α) – 3(sin²α + cos⁴α)

Hướng dẫn: Sử dụng a³ + b³; A = -1

1. b) B = 4(sin⁴α + cos⁴α) – cos⁴α

Hướng dẫn: Sử dụng a² + b² = (a + b)² – 2ab và cos2α = 1 – 2sin²a; B = 3

Công thức lượng giác mà trong đó công thức nhân đôi đóng vai trò vô cùng quan trọng trong giải toán. Cần chú ý đến các hệ quả của các công thức trên để áp dụng vào bài tập như ví dụ trong bài tập vận dụng. Hệ quả của nó cũng vô cùng quan trọng. 

Đôi khi, chỉ áp dụng hệ quả mới đưa ra được đáp án.

        Những kiến thức về lượng giác ngày nay được dạy rộng rãi và bắt buộc nằm trong chương trình giáo khoa của giáo dục Việt Nam. Thường là một phần được dạy nằm trong phần đại số của chương trình học, đôi khi nó cũng được tách riêng ra dạy sâu hơn. 

Nói về hàm lượng giác, hàm số lượng giác được dùng rộng rãi trong nhánh toán học thuần túy và trong toán học ứng dụng vào thực tế.

         Ví dụ như là được dùng để phân tích Fourier và hàm số sóng. Đây là những phần quan trọng trong nghiên cứu của nền khoa học và công nghệ hiện đại. 

• Lượng giác hình cầu nghiên cứu hình tam giác trên hình cầu, bề mặt của hằng số độ cong dương, trong hình học elip. Là một trong những nguyên tắc cơ bản và vô cùng quan trong  ngành thiên văn học và ngành hàng hải.
• Lượng giác trên một bề mặt của độ cong âm thuộc hình học Hypebol.

Phía trên là tất cả những thông tin có liên quan đến công thức nhân đôi trong lượng giác, bao gồm khái quát lượng giác, công thức nhân đôi trong lượng giác, cách chứng minh các công thức ấy, bài tập vận dụng và ý nghĩa của việc nghiên cứu và học tập về lượng giác. 

Hy vọng những kiến thức trên mà kênh tintuctuyensinh gửi đến các bạn hữu ích. Chúc các bạn thành công và may mắn!

Xem thêm:

So sánh số thứ tự thường gặp nhất hiện nay

Phép nhân là gì? Phương pháp học hiệu quả nhất

Ký hiệu mở rộng – Cách để mở rộng số dễ hiểu nhất