Những cách tính diện tích bề mặt của vật rắn dễ dàng hiệu quả

Làm thế nào để tìm diện tích bề mặt của vật rắn?

Để xác định diện tích bề mặt của một vật rắn, chúng ta lấy tổng diện tích của tất cả các bề mặt của một vật rắn 3 chiều.

Trong bài này, chúng ta sẽ thảo luận về cách tìm diện tích bề mặt của chất rắn, diện tích bề mặt của chất rắn thông thường và diện tích bề mặt của chất rắn không đều.

Diện tích bề mặt của công thức chất rắn

Chất rắn thông thường có công thức xác định để tìm diện tích bề mặt của chúng.

Các ví dụ phổ biến về chất rắn thông thường bao gồm; hình lập phương, lăng trụ, hình lập phương, hình cầu, bán cầu, hình nón và hình trụ.

Diện tích bề mặt của chất rắn thông thường

• Diện tích bề mặt của một khối rắn:

Diện tích bề mặt của một khối lập phương = 4s ²

Trong đó, s = chiều dài của cạnh.

• Diện tích bề mặt hình khối

Diện tích bề mặt của hình khối = 2lw + 2lh + 2wh

SA = 2 (lw + lh + wh)

Trong đó, l = chiều dài, w = chiều rộng và h = chiều cao của vật rắn.

• Diện tích bề mặt của hình lăng trụ đặc:

Hình lăng trụ là một vật rắn ba chiều có hai đáy là đa giác song song và đồng dạng được nối với nhau bằng các mặt hình chữ nhật. Công thức cho diện tích bề mặt của một lăng trụ phụ thuộc vào hình dạng của đáy của nó.

Công thức tổng quát cho diện tích bề mặt của hình lăng trụ = 2 × diện tích đáy + chu vi đáy × chiều cao.

SA = 2B + ph

• Diện tích bề mặt của một hình trụ đặc:

Hình trụ đặc là vật thể có hai mặt tròn song song và đồng dạng được nối với nhau bằng một mặt cong.

Diện tích bề mặt của hình trụ = 2 × diện tích hình tròn + diện tích hình chữ nhật (mặt cong)

Diện tích bề mặt của hình trụ đặc = 2πr (r + h)

• Diện tích bề mặt của một hình nón đặc:

Hình nón là một vật rắn có đáy là hình tròn được nối với một mặt cong thuôn nhọn từ đáy đến đỉnh.

Diện tích bề mặt của một hình nón đặc = Diện tích cung + diện tích hình tròn

SA = πrs + πr ²  = πr (r + s)

Trong đó s là chiều cao nghiêng của hình nón và r là bán kính của đáy hình tròn.

• Diện tích bề mặt của một kim tự tháp đặc

Một kim tự tháp có thể được định nghĩa là một vật rắn có đáy là đa giác và các mặt bên là hình tam giác. Cũng giống như một hình lăng trụ, một kim tự tháp được đặt tên theo hình dạng của đáy của nó.

Công thức tổng quát cho diện tích bề mặt của một hình chóp đặc là:

SA = Diện tích cơ sở + ½ ps

Trong đó, p = chu vi của đáy và s = ​​chiều cao nghiêng của hình chóp.

Cho hình chóp vuông, diện tích thiết diện, SA = b ²  + 2bs

Trong đó, b = chiều dài cơ sở và s = ​​chiều cao nghiêng.

• Diện tích bề mặt của một hình cầu đặc:

Diện tích bề mặt của một hình cầu, SA = 4 πr ²

Đối với bán cầu đặc, diện tích bề mặt, SA = 3πr ²

Diện tích bề mặt của chất rắn không đều

Vật thể không đều là sự kết hợp của hai hoặc nhiều vật thể thông thường. Do đó, diện tích bề mặt của một vật rắn không đều có thể được tính bằng cách cộng các diện tích bề mặt của các vật thể thông thường tạo thành nó lại với nhau.

Chúng ta hãy xem xét.

Xem thêm:

Cách tính diện tích bề mặt của một khối lập phương đơn giản nhất

Chi tiết cách tính diện tích bề mặt của một kim tự tháp dễ nhất

ví dụ 1

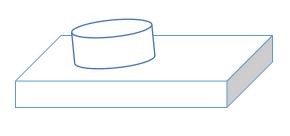
Trong sơ đồ dưới đây, bán kính và chiều cao của phần hình trụ lần lượt là 7 cm và 10 cm. Chiều dài, chiều rộng và chiều cao của phần hình chữ nhật lần lượt là 15 cm, 8 cm và 4 cm. Tính diện tích bề mặt vật rắn không đều.

Giải pháp

Diện tích bề mặt của phần hình chữ nhật = 2 (lw + lh + wh)

= 2 (15 x 8 + 15 x 4 +8 x 4)

= 2 (120 + 60 + 32)

= 2 x 212

= 424 cm ² .

Diện tích bề mặt của phần hình trụ = 2πr (r + h)

= 2 x 3,14 x 7 (7 + 10)

= 43,96 x 17

= 747,32 cm ²

Nhưng, một mặt tròn của hình trụ bị ẩn, do đó, trừ diện tích của nó cho diện tích bề mặt của hình trụ.

= 747,32 – 3,14 x 7 x 7

= 593,46 cm ²

Tổng diện tích bề mặt của vật rắn không đều = 747,32 cm ² + 593,46 cm ²

= 1.340,78 cm ² .

Ví dụ 2

Cho trước, bán kính và chiều cao của hình trụ nhỏ hơn lần lượt là 28 cm và 20 cm. Và bán kính và chiều cao của hình trụ lớn hơn lần lượt là 32 và 20 cm. Tính diện tích bề mặt của vật rắn.

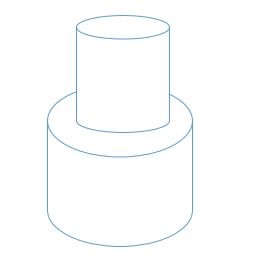
Giải pháp

Diện tích bề mặt của mặt tròn ở trên cùng = 3,14 x 28 x 28

= 2.461,76 cm ²

Diện tích bề mặt cong của hình trụ nhỏ hơn = 3,14 x 2 x 28 x 20

= 3.516,8 cm ² .

Diện tích bề mặt của đế hình tròn = 3,14 x 32 x 32

= 3.215,36 cm ²

Diện tích phần hình tròn ở đỉnh = 3.215,36 cm ² – 2.461,76 cm ²

= 753,6 cm ²

Diện tích bề mặt cong của hình trụ lớn hơn = 3,14 x 32 x 2 x 20

= 4.019,2 cm ² .

Tổng diện tích bề mặt của vật rắn = 2.461,76 + 3.516,8 + 3.215,36 + 753,6 + 4.019,2

= 13.966,72 cm ²