Diện tích tam giác – Giải thích và ví dụ chi tiết dễ hiểu nhất

Trong bài này, chúng ta sẽ cùng nhau tìm hiểu diện tích hình tam giác là gì và cách xác định diện tích các loại hình tam giác . Diện tích hình tam giác là khoảng không gian bên trong hình tam giác. Nó được đo bằng đơn vị bình phương.

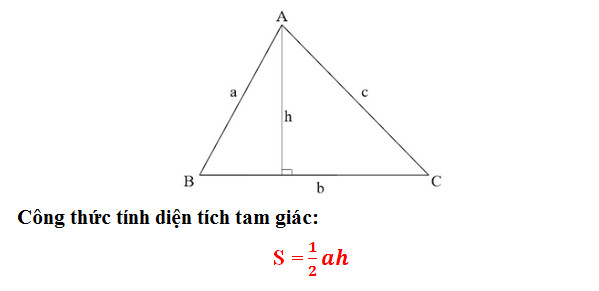
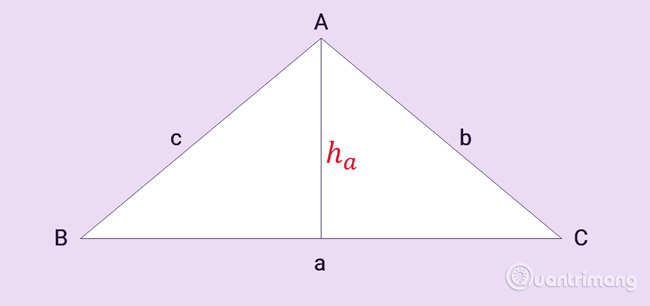
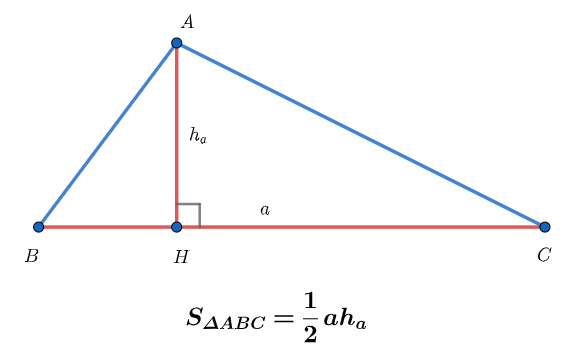
Trước khi đi vào chủ đề diện tích hình tam giác , chúng ta hãy làm quen với các thuật ngữ như cơ sở và chiều cao của hình tam giác.

Cơ sở là cạnh của một tam giác được coi là đáy. Mặt khác, đường cao của tam giác là đường vuông góc thả xuống đáy của nó từ đỉnh đối diện với đáy.

Trong hình minh họa ở trên, các đường chấm là chiều cao có thể có của △ ABC. Lưu ý rằng, mọi tam giác đều có, có thể là ba đường cao hoặc đường cao.

• Chiều cao của tam giác △ABC bằng h ₁ khi đáy là cạnh
• Chiều cao của tam giác △ABC bằng h2 khi đáy là AB
• Chiều cao của tam giác △ABC bằng h ₃ khi đáy là
• Chiều cao của tam giác △ABC có thể nằm ngoài một tam giác ( h ₄ ) bằng chiều cao h ₁ .

Từ các hình minh họa trên, có thể nhận ra các nhận xét sau:

• Chiều cao của một tam giác phụ thuộc vào đáy của nó.
• Đường vuông góc với đáy của một tam giác bằng chiều cao của tam giác đó.
• Chiều cao của một tam giác có thể nằm ngoài tam giác.

Đã thảo luận về khái niệm chiều cao và đáy của hình tam giác, bây giờ chúng ta hãy bắt tay vào cách tính diện tích hình tam giác.

Làm thế nào để tìm diện tích của một tam giác?

Diện tích của một hình chữ nhật được chúng ta biết rõ là chiều dài * chiều rộng . Điều gì sẽ xảy ra nếu chúng ta chia đôi hình chữ nhật theo đường chéo (cắt thành một nửa)? Khu vực tin tức của nó sẽ là gì? Ví dụ, một hình chữ nhật có đáy và chiều cao lần lượt là 6 đơn vị và 12 đơn vị, diện tích hình chữ nhật là 72 đơn vị hình vuông.

Bây giờ nếu bạn chia nó thành hai nửa bằng nhau (sau khi chia đôi hình chữ nhật theo đường chéo) thì diện tích của hai hình mới mỗi hình phải là 36 đơn vị hình vuông. Hai hình tin tức là hình tam giác. Điều đó có nghĩa là nếu hình chữ nhật bị cắt theo đường chéo thành hai nửa bằng nhau thì hai hình mới được tạo thành là hình tam giác, trong đó mỗi hình tam giác có diện tích bằng ½ diện tích hình chữ nhật.

Diện tích của một tam giác là tổng không gian hoặc vùng được bao bởi một tam giác cụ thể.
Diện tích của một tam giác là tích của cơ sở và chiều cao chia cho 2.

Đơn vị tiêu chuẩn để đo diện tích là mét vuông (m ² ).

Các đơn vị khác bao gồm:

• Milimét vuông (mm ²)
• Inch vuông (trong ²)
• Két vuông (km ²)
• Các thước vuông.

Diện tích của một công thức tam giác

Công thức tổng quát để tính diện tích tam giác là;

Diện tích (A) = ½ (b × h) đơn vị hình vuông, trong đó; A là diện tích, b là đáy và h là chiều cao của tam giác. Các hình tam giác có thể khác nhau về bản chất, nhưng điều quan trọng cần lưu ý là công thức này có thể áp dụng cho tất cả các hình tam giác. Các loại hình tam giác khác nhau có các công thức diện tích khác nhau.

Lưu ý: Cơ sở và chiều cao phải cùng đơn vị tức là mét, ki lô mét, cm, v.v.

Diện tích tam giác vuông

Diện tích hình tam giác = (½ × Cơ sở × Chiều cao) đơn vị hình vuông.

ví dụ 1

Tìm diện tích tam giác vuông có đáy là 9 m và chiều cao là 12m.

Giải pháp

A = ¹ / ₂ × cơ sở × chiều cao

= ¹ / ₂ × 12 × 9

= 54 cm²

Ví dụ 2

Cạnh đáy và chiều cao của tam giác vuông lần lượt là 70 cm và 8 m. Diện tích của tam giác là bao nhiêu?

Giải pháp

A = ½ × cơ sở × chiều cao

Ở đây, chúng tôi có 70 cm và 8 m. Bạn có thể chọn làm việc với cm hoặc m. Hãy tính theo đơn vị mét bằng cách đổi 70 cm sang mét.

Chia 70cm cho 100.

70/100 = 0,7m.

⇒ A = (½ × 0,7 × 8) m ²

⇒ A = (½ x 5,6) m ²

⇒ A = 2,8m ²

Diện tích tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc bằng nhau. Công thức tính diện tích tam giác cân là;

⇒A = ½ (cơ sở × chiều cao).

Khi không cho trước chiều cao của tam giác cân, thì công thức sau được sử dụng để tìm chiều cao:

Chiều cao = √ (a ²  – b ^2/4 )

Ở đâu;

b = cơ sở của tam giác

a = Độ dài cạnh hai cạnh bằng nhau.

Do đó, diện tích tam giác cân có thể là;

⇒A = ½ [√ (a ²  – b ^2/4  ) × b]

Ngoài ra, diện tích của một tam giác vuông cân được cho bởi:

A = ½ × a ² , trong đó a = Độ dài cạnh của hai cạnh bằng nhau

Ví dụ 3

Tính diện tích hình tam giác cân có đáy là 12 mm và chiều cao là 17 mm.

Giải pháp

⇒A = ½ × cơ sở × chiều cao

⇒ 1/2 × 12 × 17

⇒ 1/2 × 204

= 102 mm ²

Ví dụ 4

Tìm diện tích của một tam giác cân có độ dài các cạnh là 5m và 9m

Giải pháp

Cho cơ sở, b = 9 m và a = 5m.

⇒ A = ½ [√ (a ²  – b ^2/4  ) × b]

⇒ ½ [√ (5 ²  – 9 ^2/4  ) × 9]

= 9,81m ²

Diện tích tam giác đều

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc trong bằng nhau. Diện tích của tam giác đều là;

A = (a ² √3) / 4

Trong đó, a = độ dài của các cạnh.

Ví dụ 5

Tính diện tích của một tam giác đều có cạnh là 4 cm.

Giải pháp

⇒ A = (a ^2/4 ) √3

⇒ (4 ^2/4 ) √3

⇒ (16/4) √3

= 4√3 cm ²

Ví dụ 6

Tìm diện tích của một tam giác đều có chu vi là 84 mm.

Giải pháp

Chu vi hình tam giác đều = 3a.

⇒ 3a = 84 mm

⇒ a = 84/3

⇒ a = 28 mm

Diện tích = (a ^2/4 ) √3

⇒ (28 ^2/4 ) √3

= 196√3 mm ²

Diện tích tam giác vô hướng

Tam giác vô hướng là tam giác có 3 độ dài cạnh khác nhau và 3 góc khác nhau. Diện tích của một tam giác vô hướng có thể được tính bằng công thức Heron.
Công thức của Heron được đưa ra bởi;
⇒ Diện tích = √ {p (p – a) (p – b) (p – c)}

trong đó ‘p’ là nửa chu vi và a, b, c là độ dài các cạnh.

⇒ p = (a + b + c) / 2

Ví dụ 7
Tính diện tích hình tam giác có độ dài các cạnh là 18mm, 20mm và 12mm.

Giải pháp

⇒ p = (a + b + c) / 2
Thay các giá trị của a, b và c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Diện tích = √ {p (p – a) (p – b) (p – c)}
= √ {25 x ( 25 – 12) x (25 – 18) x (25 – 20)}
= √ (25 x 13 x 7 x 5)
= 5√455 mm ²

Xem thêm:

Các góc của một tam giác và những giải thích chi tiết nhất

Các loại hình tam giác và tất tần tật thông tin về nó