Chức năng khu vực

Hãy xem xét một hàm số f theo x xác định trong khoảng [a, b]. Tích phân của f (x) giữa điểm a và b tức là∫baf( x ) d( x ),  I là khu vực mà tôi s bao bọc bởi đường cong y = f (x) và các đường x = a, x = b và x – trục∫xaf( x ) dx. mô tả diện tích của vùng được tô màu nâu trong đó x là một điểm nằm trong khoảng [a, b]. Giả sử rằng các giá trị mà hàm này nhận được là không âm, đồ thị sau đây mô tả f theo x.

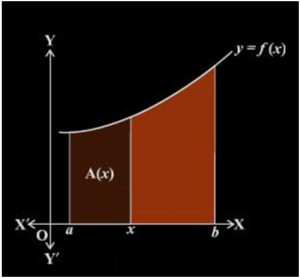
A (x) được gọi là hàm diện tích được cho là;

Tùy thuộc vào điều này, định lý cơ bản của Giải tích có thể được định nghĩa là hai định lý như được nêu dưới đây:

Định lý cơ bản đầu tiên của phép tính tích phân (Phần 1)

Phần đầu tiên của định lý giải tích đôi khi được gọi là định lý cơ bản đầu tiên của giải tích. Nó khẳng định rằng một trong các đạo hàm phản chứng (cũng có thể được gọi là tích phân bất định) nói rằng F, của một số hàm f, có thể nhận được dưới dạng tích phân của f với một giới hạn tích phân biến đổi. Từ điều này, chúng ta có thể nói rằng có thể có các chất chống nhiễm trùng cho một chức năng liên tục.

Phát biểu: Gọi f là hàm liên tục trên khoảng đóng [a, b] và gọi A (x) là hàm diện tích. Khi đó A ′ (x) = f (x), với mọi x ∈ [a, b].

Hoặc là

Gọi f là một hàm có giá trị thực liên tục xác định trên một khoảng đóng [a, b]. Gọi F là hàm được xác định, với mọi x trong [a, b], bởi:

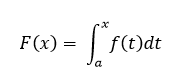
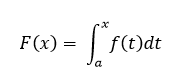
Khi đó F liên tục đồng nhất trên [a, b] và khả vi trên khoảng mở (a, b), và

F ‘(x) = f (x) ∀ x ∈ (a, b)

Ở đây, F ‘(x) là một hàm đạo hàm của F (x).

Định lý cơ bản thứ hai của phép tính tích phân (Phần 2)

Định lý cơ bản thứ hai của giải tích phát biểu rằng, nếu hàm “f” liên tục trên khoảng đóng [a, b] và F là một tích phân không xác định của hàm “f” trên [a, b], thì hàm cơ bản thứ hai định lý giải tích được định nghĩa là:

F (b) – F (a) = ∫ _a ^b f (x) dx

Ở đây RHS của phương trình chỉ ra tích phân của f (x) đối với x.

f (x) là tích phân.

dx là tác nhân tích hợp.

‘a’ chỉ giới hạn trên của tích phân và ‘b’ chỉ giới hạn dưới của tích phân.

Hàm của một tích phân xác định có một giá trị duy nhất. Tích phân xác định của một hàm có thể được mô tả như là một giới hạn của một tổng. Nếu tồn tại một đạo hàm F của hàm trong khoảng [a, b] thì tích phân xác định của hàm là hiệu giữa các giá trị của F, tức là F (b) – F (a).

Nhận xét về Định lý cơ bản thứ hai của Giải tích

• Phần thứ hai của định lý cơ bản của giải tích cho chúng ta biết rằng ∫ _a ^b f (x) dx = (giá trị của đạo hàm F của “f” ở giới hạn trên b) – (cùng giá trị đạo hàm ở giới hạn dưới a).
• Định lý này rất có lợi vì nó cung cấp cho chúng ta một phương pháp ước lượng tích phân xác định nhanh chóng hơn mà không cần xác định giới hạn của tổng.
• Khi ước lượng một tích phân xác định, phép toán cơ bản là tìm một hàm có đạo hàm bằng tích phân. Tuy nhiên, quá trình này sẽ củng cố mối quan hệ giữa phân hóa và tích hợp.
• Trong biểu thức ∫ _a ^b f (x) dx, hàm f (x) hay nói “f” phải xác định rõ và liên tục trong khoảng [a, b].

Hệ quả

Định lý cơ bản thường được áp dụng để tính tích phân xác định của hàm f mà một đạo hàm F đã biết. Đặc biệt, nếu f là một hàm liên tục có giá trị thực trên [a, b] và F là một đạo hàm của f trong [a, b] thì

∫baf( t ) dt = F( b ) – F( a )

Hệ quả cho phép liên tục trên khoảng hoàn chỉnh.

Làm thế nào để tính tích phân xác định?

Dưới đây là các bước để tính toán ∫baf( x ) dx

• Xác định tích phân bất định của f (x) là F (x). Cần lưu ý rằng hằng số tùy ý không được xem xét trong khi tính các tích phân xác định vì nó tự hủy, tức là

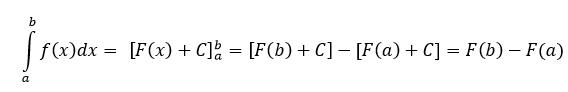
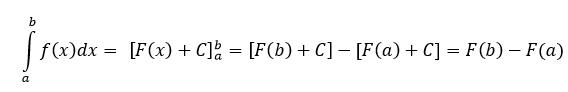
• Tính F (b) – F (a) cho ta giá trị của tích phân xác định của f theo x nằm giữa khoảng đóng [a, b].

Các ví dụ

Q.1: Đánh giá tích phân: ∫ ₂ ³  y ² dy
Giải pháp: Hãy I = ∫ ₂ ³  y ² dy
Như chúng ta đã biết,
∫y ² dy = y ³ /3 = F (y)
Vì vậy, bằng cách lý giải tích cơ bản thứ hai , chúng tôi biết;
I = F (3) – F (2) = 27/3 – 8/3 = 19/3

Q.2: Đánh giá tích phân: ∫ ₁ ² [ydy / (y + 1) (y + 2)] Lời
giải: Bằng phân số riêng, chúng ta có thể tính thừa số của số hạng dưới tích phân.
y / [(y + 1) (y + 2)] = [-1 / (y + 1)] + [2 / (y + 2)] Vì vậy,
∫y / [(y + 1) (y + 2 )] = -log | y + 1 | + 2log | x + 2 | = F (y)
Do đó, theo định lý cơ bản của giải tích phần 2, chúng ta nhận được;
I = F (2) -F (1) = [- log 3 + 2 log 4] – [- log 2 + 2 log 3] I = – 3 log 3 + log 2 + 2 log 4
I = log (32 / 27)

Vấn đề thực hành

Nhận thêm câu hỏi tại đây để thực hành để hiểu khái niệm một cách nhanh chóng.

Đánh giá bằng cách sử dụng định lý cơ bản của giải tích:

1. ∫Số Pi40s tôin32 t c o s 2 t d  t
2. ∫431xdx
3. ∫206 x + 3x2– 4dx