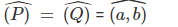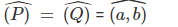Định nghĩa, cách xác định của Góc giữa hai mặt phẳng

Góc giữa hai mặt phẳng là gì? Cách xác định Góc giữa hai mặt phẳng ra sao? qui định tính góc như thế nào? Mời Anh chị em hãy cùng Tintuctuyensinh theo dõi bài viết dưới đây nhé.

Trong bài viết đưới đây tintuctuyensinh giới thiệu tới Anh chị em cục bộ tri thức về góc giữa 2 mặt phẳng như: khái niệm, cách xác định, nguyên tắc và một số bài tập ứng dụng. Qua tài liệu này giúp Anh chị lớp 11 hối hả nắm vững kiến thức để học tốt Hình học 11.

1. định nghĩa Góc giữa hai mặt phẳng

– Khái niệm: Góc giữa hai mặt phẳng là gì? Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với nhị mặt phẳng đó.

Trong không gian 3 chiều, góc giữa 2 mặt phẳng còn được gọi là ‘góc khối’, là phần không gian bị giới hạn vì 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng.

– Tính chất: Từ định nghĩa trên ta có:

• Góc giữa 2 mặt phẳng đồng thời bằng 0 độ,
• Góc giữa 2 mặt phẳng trùng nhau bằng 0 độ.

2. Cách xác định Góc giữa hai mặt phẳng

Để có thân xác định đúng mực góc giữa 2 mặt phẳng game thủ ứng dụng những cách sau:

Gọi P là mặt phẳng 1, Q là mặt phẳng 2

Trường hợp 1: nhì mặt phẳng (P), (Q) song song hoặc trùng nhau thì góc của 2 mặt phẳng bằng 0,

Trường hợp 2: nhì mặt phẳng (P), (Q) không đồng thời hoặc trùng nhau.

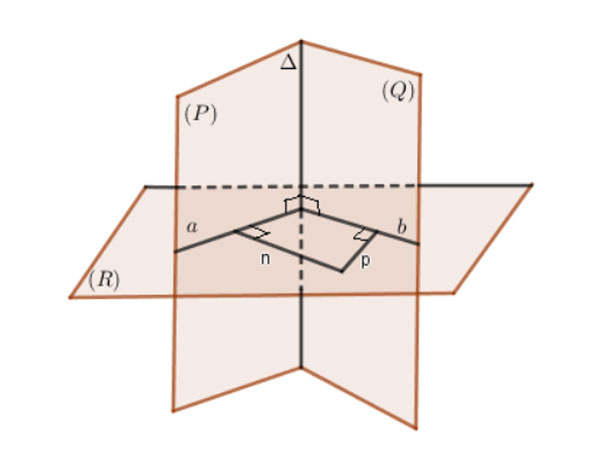
Cách 1: Dựng 2 đường thẳng n và p vuông góc tuần tự với 2 mặt phẳng (P), (Q). Khi đó góc giữa 2 mặt phẳng (P), (Q) là góc giữa 2 đường thẳng n và p.

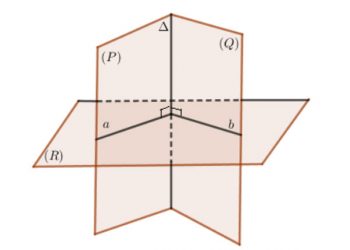
Cách 2: Để xác định góc giữa 2 mặt phẳng trước tiên bạn cần xác định giao tuyến Δ∆của 2 mặt phẳng (P) và (Q). Tiếp theo, game thủ tìm một mặt phẳng (R) vuông góc với giao tuyến Δ∆của 2 mặt phẳng (P), (Q) và cắt 2 mặt phẳng tại các giao tuyến a, b.

⇒Góc giữa 2 mặt phẳng (P), (Q) là góc giữa a và b.

3. phương pháp tính Góc giữa hai mặt phẳng

Có 2 nguyên lý bạn có thể vận dụng để tính góc giữa 2 mặt phẳng:

nguyên lý 1: sử dụng hệ thức lượng trong tam giác vuông, định lý hàm số sin, hàm số cos.

thí dụ 1: Cho hình chóp bốn giác đều S.ABCD có đáy là ABCD và độ dài các cạnh đáy bằng a, SA = SB = SC = SD = a. Tính cos góc giữa nhị mặt phẳng (SAB) và (SAD).

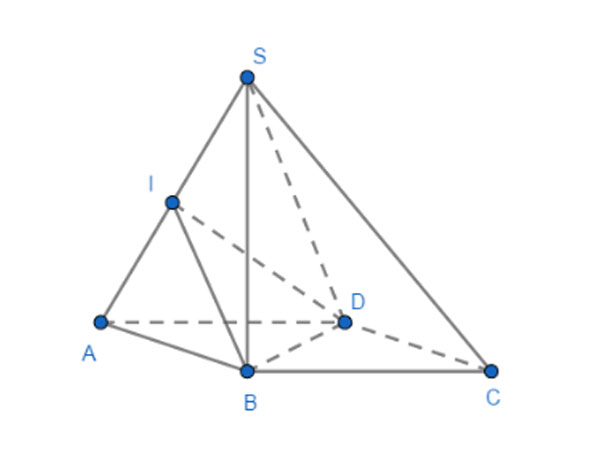
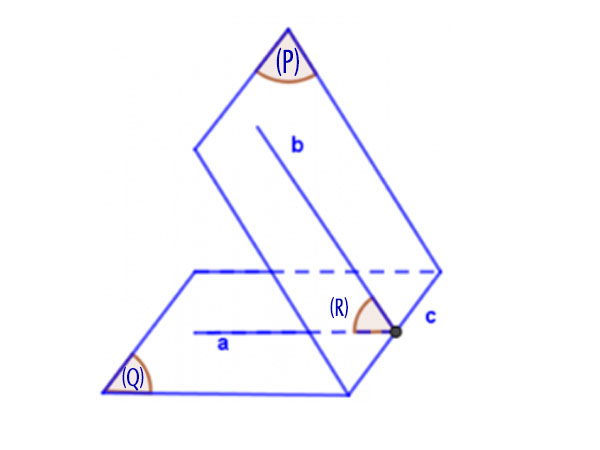
lý lẽ 2: Dựng mặt phẳng phụ (R) vuông góc với giao tuyến c nhưng mà (Q) giao với (R) = a, (P) giao với (R) = b.

Suy ra