• Tam giác Scalene
• Tam giác cân
• Tam giác đều
• Hình tam giác có góc nhọn
• Hình tam giác có góc xiên
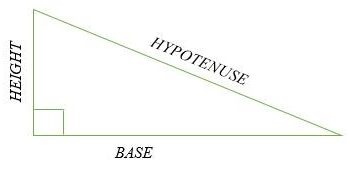
• Tam giác vuông góc

Trọng tâm là một tính chất quan trọng của một tam giác. Hãy để chúng tôi thảo luận về định nghĩa của centroid, công thức, thuộc tính và centroid cho các hình dạng hình học khác nhau một cách chi tiết.

Định nghĩa Tâm

Tâm là điểm chính giữa của vật thể. Điểm mà ba trung tuyến của tam giác cắt nhau được gọi là trọng tâm của tam giác . Nó cũng được xác định là giao điểm của cả ba trung tuyến. Đường trung tuyến là đoạn thẳng nối trung điểm của một cạnh và đỉnh đối diện của tam giác. Trọng tâm của tam giác chia cắt đường trung tuyến theo tỷ lệ 2: 1. Có thể tìm được bằng cách lấy trung bình cộng của các điểm tọa độ x và các điểm tọa độ y của tất cả các đỉnh của tam giác.

Định lý Tâm

Định lý Tâm phát biểu rằng trọng tâm của tam giác nằm bằng 2/3 khoảng cách từ đỉnh đến trung điểm của các cạnh.

Giả sử PQR là tam giác có trọng tâm là V. S, T và U lần lượt là trung điểm các cạnh của tam giác PQ, QR và PR. Do đó theo định lý;

QV = 2/3 QU, PV = 2/3 PT và RV = 2/3 RS

Tâm của một tam giác góc phải

Trọng tâm của một tam giác vuông là giao điểm của ba trung tuyến, được vẽ từ các đỉnh của tam giác đến trung điểm của các cạnh đối diện.

Centroid of a Square

Điểm mà các đường chéo của hình vuông cắt nhau là tâm của hình vuông. Như chúng ta đã biết, hình vuông có tất cả các cạnh của nó bằng nhau. Do đó, rất dễ dàng để xác định vị trí trung tâm trong đó. Xem hình bên dưới, trong đó O là tâm của hình vuông.

Ngoài ra, hãy đọc:

Thuộc tính của Tâm

Các thuộc tính của Tâm như sau:

• Centroid là tâm của vật thể.
• Nó là tâm của trọng lực.
• Nó phải luôn luôn nằm bên trong đối tượng.
• Nó là điểm đồng thời của các phương tiện truyền thông.

Công thức Tâm

Hãy xem xét một tam giác. Nếu ba đỉnh của tam giác là A (x ₁ , y ₁ ), B (x ₂ , y ₂ ), C (x ₃ , y ₃ ) thì trọng tâm của tam giác có thể được tính bằng cách lấy trung bình cộng của X. và Y tọa độ điểm của cả ba đỉnh. Do đó, trọng tâm của một tam giác có thể được viết là:

Tâm của tam giác = ((x ₁ + x ₂ + x ₃ ) / 3, (y ₁ + y ₂ + y ₃ ) / 3)

Công thức Tâm cho các hình dạng khác nhau

Ở đây, danh sách công thức centroid được đưa ra cho các hình dạng hình học khác nhau.

Hình dạng	Nhân vật	NS	ȳ	Khu vực
Khu tam giác		–	h / 3	bh / 2
Diện tích hình tròn		4r / 3π	4r / 3π	πr 2 /4
Vùng bán nguyệt		0	4r / 3π	πr 2 /2
Diện tích hình elip		4a / 3π	4b / 3π	πab / 4
Vùng bán elip		0	4b / 3π	πab / 2
Khu vực bán đồng hóa		3a / 8	3h / 5	2ah / 3
Khu vực hình parabol		0	3h / 5	4ah / 3
Spandrel parabol		3a / 4	3h / 10	à / 3

Ví dụ về tính toán Tâm

Tìm các ví dụ đã giải dưới đây, để tìm trọng tâm của tam giác với các giá trị đỉnh đã cho.

Câu 1: Tìm trọng tâm của tam giác có các đỉnh là A (2, 6), B (4, 9) và C (6,15).

Dung dịch:

Được cho:

A (x ₁ , y ₁ ) = A (2, 6)

B (x ₂ , y ₂ ) = B (4,9)

C (x ₃ , y ₃ ) = C (6,15)

Chúng ta biết rằng công thức tìm trọng tâm của tam giác là = ((x ₁ + x ₂ + x ₃ ) / 3, (y ₁ + y ₂ + y ₃ ) / 3)

Bây giờ, thay thế các giá trị đã cho trong công thức

Tâm của tam giác = ((2 + 4 + 6) / 3, (6 + 9 + 15) / 3)

= (12/3, 30/3)

= (4, 10)

Do đó, trọng tâm của tam giác đối với các đỉnh A (2, 6), B (4,9) và C (6,15) đã cho là (4, 10).

Câu 2: Tìm trọng tâm của tam giác có các đỉnh là A (1, 5), B (2, 6) và C (4, 10).

Giải: Cho, A (1, 5), B (2, 6) và C (4, 10) là các đỉnh của tam giác ABC.

Bằng công thức của centroid mà chúng ta biết;

Centroid = ((x ₁ + x ₂ + x ₃ ) / 3, (y ₁ + y ₂ + y ₃ ) / 3)

Đặt các giá trị, chúng tôi nhận được;

Centroid = (1 + 2 + 4) / 3, (5 + 6 + 10) / 3

= (7/3, 21/3)

= (7 / 3,7)

Do đó, trọng tâm của tam giác có các đỉnh A (1, 5), B (2, 6) và C (4, 10) là (7/3, 7).

Câu 3: Nêu các đỉnh của tam giác PQR là (2, 1), (3, 2) và (-2, 4). Sau đó, tìm trọng tâm của nó.

Giải: Cho (2, 1), (3, 2) và (-2, 4) là các đỉnh của tam giác pQR.

Bằng công thức của centroid mà chúng ta biết;

Centroid = ((x ₁ + x ₂ + x ₃ ) / 3, (y ₁ + y ₂ + y ₃ ) / 3)

Đặt các giá trị, chúng tôi nhận được;

Centroid, O = (2 + 3-2) / 3, (1 + 2 + 4) / 3

O = (3/3, 7/3)

O = (1, 7/3)

Do đó, trọng tâm của tam giác có các đỉnh (2, 1), (3, 2) và (-2, 4) là (1, 7/3).