Quy tắc Cosine và những cách giải hay nhất hiện nay

Chúng ta đã xem trong phần trước quy tắc sin giúp chúng ta tính góc thiếu hoặc thiếu cạnh khi biết hai cạnh và một góc như thế nào hoặc khi biết hai góc và một cạnh.

Nhưng bạn sẽ làm gì khi bạn chỉ có ba cạnh của một tam giác và bạn cần tìm tất cả các góc?

Vấn đề đó đã được giải quyết trong 15 ^ngày thế kỷ, khi một nhà toán học Ba Tư, Jamshid al-Kashi trình bày định lý cos trong một hình thức thích hợp cho tam giác. Ở Pháp, nó vẫn được gọi là Theoreme d’Al-Kashi .

Trong bài viết này, bạn sẽ tìm hiểu về:

• Định luật cosin,
• cách áp dụng định luật cosin để giải quyết vấn đề và,
• định luật công thức côsin.

Định luật Cosin là gì?

Định luật côsin , còn được gọi là quy tắc côsin là một công thức liên hệ độ dài ba cạnh của một tam giác với côsin.

Quy tắc cosine hữu ích theo hai cách:

• Quy tắc côsin có thể được sử dụng để tìm ba góc chưa biết của tam giác nếu biết độ dài ba cạnh của tam giác đã cho.
• Quy tắc cosin cũng có thể được sử dụng để tìm độ dài cạnh thứ ba của một tam giác nếu độ dài hai cạnh và góc giữa chúng đã biết.

Định luật công thức cosin

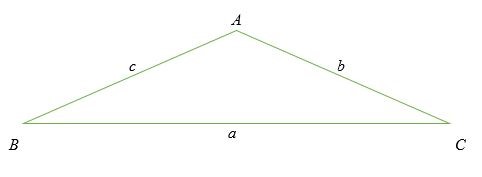
Xét một tam giác ABC xiên được hiển thị bên dưới. Một tam giác xiên là một tam giác không vuông. Hãy nhớ rằng độ dài các cạnh được dán nhãn bằng chữ thường trong khi các góc được dán nhãn bằng chữ in hoa.

Cũng lưu ý rằng, mỗi góc có độ dài cạnh đối diện được gắn nhãn bằng cùng một chữ cái.

Định luật cosin phát biểu rằng:

⇒ (a) ²  = [b ²  + c ² – 2bc] cos ( A )

⇒ (b) ²  = [a ²  + c ²  – 2ac] cos ( B )

⇒ (c) ²  = [a ²  + b ²  – 2bc] cos ( C )

Bạn nhận thấy rằng, phương trình c ²  = a ²  + b ²  – 2bc cos ( C ) giống với Định lý Pitago, ngoại trừ các số hạng cuối cùng, “- 2bc cos ( C ).” Vì lý do này, chúng ta có thể nói rằng Định lý Pitago là một đặc biệt của quy tắc sin.

Xem thêm:

Cách học định lý Tam giác Sum hiệu quả nhất hiện nay

Hình tam giác vuông đặc biệt – Giải thích & Ví dụ hay nhất

Chứng minh định luật côsin

Quy tắc côsin có thể được chứng minh bằng cách xem xét trường hợp của một tam giác vuông. Trong trường hợp này, hãy thả một đường vuông góc từ điểm A đến điểm O trên cạnh BC.

Cho cạnh AM là h.

Trong tam giác vuông ABM , cosin của góc B cho bởi;

Cos ( B ) = Liền kề / Hypotenuse = BM / BA

Cos ( B ) = BM / c

BM = c cos ( B )

Cho rằng BC = a, do đó, MC được tính là;

MC = a – BM

 = a – c cos ( B ) ……………………………………………… (i)

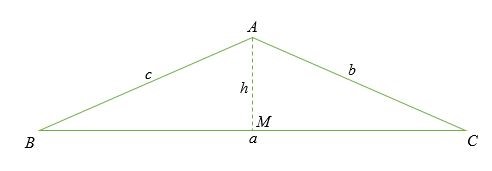
Trong tam giác ABM, sin của góc B được cho bởi;

Sine B = Đối diện / Hypotenuse = h / c

h = c sin B …………………………………………………… (ii)

Bằng cách áp dụng định lý Pitago trong tam giác vuông AMC , chúng ta có,

AC ² = AM ² + MC ² ……………………………………………… (iii)

Thay phương trình (i) và (ii) vào phương trình (iii).

b ² = (c sin B) ² + ( a – c Cos B ) ²

b ² = c ² sin ² B + a ² – 2ac Cos B + c ² Cos ² C

Sắp xếp lại phương trình trên:

b ² = c ² sin ² B + c ² Cos ² C + a ² – 2ac Cos B

Bao thanh toán.

b ² = c ² (sin ² B + Cos ² C ) + a ² – 2ac Cos B

Nhưng, từ nhận dạng lượng giác, chúng ta biết rằng,

sin ² θ + cos ² θ = 1

Do đó, b ² = c ² + a ² – 2ac Cos B

Do đó, định luật cosin được chứng minh.

Làm thế nào để sử dụng Quy tắc Cosine?

Nếu bạn cần tìm độ dài các cạnh của một tam giác, chúng ta sử dụng quy tắc côsin ở dạng;

⇒ (a) ²  = [b ²  + c ² – 2bc] cos ( A )

⇒ (b) ²  = [a ²  + c ²  – 2ac] cos ( B )

⇒ (c) ²  = [a ²  + b ²  – 2bc] cos ( C )

Và nếu chúng ta cần tìm kích thước của một góc, chúng ta sử dụng quy tắc cosin của dạng;

⇒ cos A = (b ²  + c ²  – a ² ) / 2bc

⇒ cos B = (a ²  + c ² – b ² ) / 2ac

⇒ cos C = (a ²  + b ² – c ² ) / 2ab

Bây giờ chúng ta hãy kiểm tra sự hiểu biết của chúng ta về quy tắc cosin bằng cách thử một vài bài toán ví dụ.

ví dụ 1

Tính độ dài cạnh AC của tam giác dưới đây.

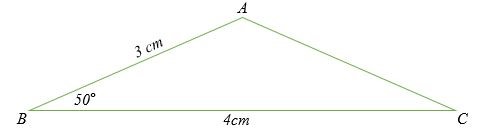
Giải pháp

Bởi vì chúng tôi muốn tính chiều dài, do đó chúng tôi sẽ sử dụng

quy tắc côsin ở dạng;

⇒ (b) ²  = [a ²  + c ²  – 2ac] cos ( B )

Bằng cách thay thế, chúng tôi có,

b ²  = 4 ²  + 3 ²  – 2 x 3 x 4 cos ( 50 )

b ² = 16 + 9 – 24cos50

= 25 – 24cos 50

b ² = 9,575

Xác định căn bậc hai của cả hai vế để nhận được,

b = √9.575 = 3.094.

Do đó, độ dài AC = 3,094 cm.

Ví dụ 2

Tính tổng ba góc của tam giác dưới đây.

Giải pháp

Vì độ dài ba cạnh của tam giác đã cho nên ta cần tìm số đo của ba góc A, B và C. Ở đây, ta sẽ sử dụng quy tắc côsin ở dạng;

⇒ Cos (A ) = [b ²  + c ²  – a ² ] / 2bc

⇒ Cos (B) = [a ²  + c ² – b ² ] / 2ac

⇒ Cos ( C) = [a ²  + b ² – c ² ] / 2ab

Giải cho góc A:

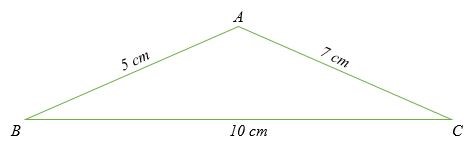
Cos A = (7 ²  + 5 ²  – 10 ² ) / 2 x 7 x 5

Cos A = (49 + 25 – 100) / 70

Cos A = -26/70

Cos A = – 0,3714.

Bây giờ, xác định nghịch đảo cos của – 0,3714.

A = Cos ^-1 – 0,3714.

A = 111,8 °

Giải cho góc B:

Bằng cách thay thế,

cos B = (10 ²  + 5 ² – 7 ² ) / 2 x 10 x 7

Đơn giản hóa.

Cos B = (100 + 25 – 49) / 140

Cos B = 76/140

Xác định nghịch đảo cos của 76/140

B = 57,12 °

Giải cho góc C:

Bằng cách thay thế,

cos C = (10 ²  + 7 ² – 5 ² ) / 2 x 10 x 7

Cos C = (100 + 49 – 25) / 140

Cos C = 124/140

Xác định cos nghịch đảo của 124/140.

C = 27,7 °

Do đó, ba góc của tam giác là; A = 111,8 °, B = 57,12 ° và C = 27,7 °.