Sử dụng công thức này, chúng ta có thể tìm thấy khoảng cách giữa hai điểm bất kỳ trong hình học và trong cuộc sống thực. Ví dụ: tìm khoảng cách giữa hai thành phố hoặc hai điểm bất kỳ trên trái đất trên bản đồ.

Tọa độ của một điểm là gì?

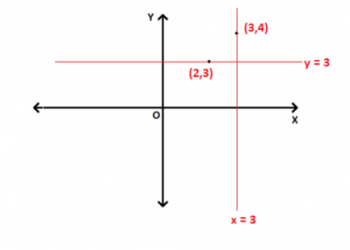
Trong hình học Euclide, chúng ta đã xem xét các điểm nằm trong mặt phẳng. Các điểm này được xác định bởi tọa độ của chúng dọc theo trục x và trục y. Do đó, tọa độ của một điểm là một cặp giá trị xác định chính xác vị trí của điểm đó trong mặt phẳng tọa độ.

Trong hình trên, tọa độ của điểm P trong mặt phẳng hai chiều là (x, y). Có nghĩa là điểm, P cách trục y đơn vị x và y cách trục x đơn vị.

Tọa độ của một điểm trên trục x có dạng (a, 0), trong đó a là khoảng cách của điểm đó từ gốc tọa độ và trên trục y có dạng (0, a), trong đó a là khoảng cách của điểm so với gốc tọa độ.

Khoảng cách giữa hai điểm – Sử dụng định lý Pythagoras

Hãy xem xét tình huống sau đây.

Một cậu bé đi về phía bắc 30 mét rồi rẽ sang phía đông và đi thêm 40 mét nữa. Làm thế nào để chúng ta tính khoảng cách ngắn nhất giữa địa điểm ban đầu và địa điểm cuối cùng?

Hình ảnh đại diện cho tình huống trên là:

Điểm ban đầu là A và điểm cuối cùng là C. Khoảng cách giữa các điểm A, B là 30 m và giữa các điểm B, C là 40 m.

Khoảng cách ngắn nhất giữa hai điểm A và C là AC. Khoảng cách này được tính bằng cách sử dụng định lý Pythagoras như sau.

AC ²  = AB ² + BC ²

A C = = 50 m302 + 402———√

Do đó, chúng tôi có khoảng cách giữa điểm đầu và điểm cuối. Tương tự, khoảng cách giữa hai điểm trong một mặt phẳng tọa độ cũng được tính bằng cách sử dụng định lý Pitago hoặc định lý tam giác vuông.

Trước khi đi vào công thức tính khoảng cách giữa hai điểm trong mặt phẳng tọa độ, chúng ta hãy hiểu thế nào là tọa độ điểm và cách xác định vị trí của chúng trong mặt phẳng Descartes.

Công thức khoảng cách cho hai điểm

Như chúng ta đã học, công thức khoảng cách của hai điểm trong mặt phẳng được cho bởi:

PQ =(x2–x1)2+ (y2–y1)2——————√

Trong đó P và Q là hai điểm riêng biệt

Hãy để chúng tôi xem, làm thế nào công thức này đến.

Bằng chứng:

Giả sử ta có hai điểm P (x ₁ , y ₁ ) và Q (x ₂ , y ₂ ) trong mặt phẳng tọa độ. Hãy để chúng tôi biểu diễn những điểm này trong hình.

Lưu ý rằng chúng ta đã lấy điểm P và Q trong chính góc phần tư đầu tiên. Điều gì sẽ xảy ra nếu các điểm nằm trong các góc phần tư khác? Như bạn sẽ thấy trong cuộc thảo luận sau đây, công thức cuối cùng vẫn giữ nguyên, bất kể P và Q nằm trong góc phần tư nào.

PS, QT vuông góc với trục x và PR song song với trục x.

Khoảng cách giữa hai điểm P và Q được tính như sau:

S và T là điểm trên trục x lần lượt là điểm cuối của hai đoạn thẳng song song PS và QT.

⇒ PR = ST

Tọa độ của S và T lần lượt là (x ₁ , 0) và   (x ₂ , 0).

OS  =  x ₁  và OT  = x ₂

ST  = OT – OS  = x ₂  – x ₁  = PR

Tương tự,

PS = RT

QR = QT – RT = QT – PS = y ₂  – y ₁

Theo định lý Pythagoras,

PQ ²  = PR ²  + QR ²

PQ = √ [ (x ₂ – x ₁ ) ² + (y ₂ – y ₁ ) ² ]

Vì thế,

Khoảng cách giữa hai điểm (x ₁ , y ₁ )  và (x ₂ , y ₂ )  là:

PQ =(x2–x1)2+ (y2–y1)2——————√

Nó được gọi là công thức khoảng cách.

Quan sát thấy (x ₂ – x ₁ ) ²   là bình phương của hiệu x – tọa độ của P và Q và luôn dương. Điều tương tự cũng có thể được nói về (y ₂ – y ₁ ) ²  . Sử dụng điểm này và cố gắng tự xem tại sao công thức vẫn giữ nguyên cho bất kỳ tọa độ nào của P và Q, trong bất kỳ góc phần tư nào.

Khoảng cách giữa một điểm từ điểm gốc

Khoảng cách từ điểm gốc đến một điểm trong mặt phẳng sẽ là bao nhiêu? Giả sử một điểm P (x, y) trong mặt phẳng xy như hình bên dưới:

Hãy tính khoảng cách giữa điểm P và gốc tọa độ. P cách trục y đơn vị x và cách trục x đơn vị.

Theo định lý Pythagoras,

OP ²  = x ²  + y ²

O P =x2 + y2——-√

Do đó khoảng cách giữa bất kỳ điểm nào (x, y) trong mặt phẳng xy và điểm gốc (0, 0) là  .x2 + y2——-√

Ngoài ra, hãy đọc:

Các ví dụ đã giải quyết

Ví dụ 1: Tìm giá trị của a, nếu khoảng cách giữa hai điểm P (3, -6) và Q (-3, a) là 10 đơn vị.

Giải pháp:

Cho các điểm đã cho là:

P (3, -6) = (x ₁ , y ₁ )

Q (-3, a) = (x ₂ , y ₂ )

Sử dụng công thức khoảng cách,

Khoảng cách giữa các điểm P (3, -6) và Q (-3, a) là:

[ (-3 – 3) ²  + (a + 6) ² ] = 10 đơn vị (đã cho)

Bình phương trên cả hai vế của phương trình,

(-6) ²  + (a + 6) ²  = 100

(a + 6) ²  = 100 – 36  = 64 

Bắt rễ cả hai bên, chúng tôi nhận được;

a + 6 = ± 8

Trường hợp I: Xét +8,

a + 6 = 8,

a = 8 – 6 = 2

Trường hợp II: Xét -8

a + 6  = -8

a = -8 – 6

a = -14

Do đó, tọa độ hoặc là P (3, -6) và Q (-3, 2) hoặc P (3, -6) và Q (-3, -14).

Ví dụ 2: Tìm quan hệ giữa x và y sao cho điểm (x, y) cách đều các điểm (7, 1) và (3, 5).

Giải: Gọi P (x, y) là điểm cách đều các điểm A (7, 1) và B (3, 5).

Được,

AP = BP

⇒ AP ²  = BP ²
(x – 7) ²  + (y – 1) ²  = (x – 3) ²  + (y – 5) ²  (theo công thức khoảng cách)
x ²  – 14x + 49 + y ²  – 2y + 1 = x ²  – 6x + 9 + y ²  – 10y + 25

-14x + 50 – 2y + 6x + 10y – 34 = 0

-8x + 8y = -16
x – y = 2
Đây là quan hệ bắt buộc giữa x và y.

Ví dụ 3: Tìm một điểm trên trục y cách đều các điểm A (6, 5) và B (- 4, 3).

Giải: Ta biết rằng một điểm trên trục y có dạng (0, y). Vì vậy, để điểm P (0, y) cách đều A và B. Khi đó:

AP = BP

⇒ AP ²  = BP ²

(6 – 0) ²  + (5 – y) ²  = (- 4 – 0) ²  + (3 – y) ²
36 + 25 + y ² – 10y = 16 + 9 + y ²  – 6y

61 – 10y = 25 – 6y

⇒ 10y – 6y = 61 – 25
⇒ 4y = 36
⇒ y = 9

Vì vậy, điểm yêu cầu là (0, 9).

Xác minh:

AP =  √ [(6 – 0) ²  + (5 – 9) ² ]

= √ (36 + 16)

= √52

BP =   √ [(- 4-0) ² + (3-9) ² ]

= √ (16 + 36)

= √52

Do đó, chúng tôi kết luận rằng, điểm (0, 9) cách đều hai điểm cho trước.

Khoảng cách giữa hai điểm trong 3D

Khoảng cách giữa hai điểm A (x ₁ , y ₁ , z ₁ ) và B (x ₂ , y ₂ , z ₂ ) trong một mặt phẳng ba chiều được cho bởi công thức:

A B =(x2–x1)2+ (y2–y1)2+ (z2–z1)2—————————-√

Đây,

(x ₂ – x ₁ ) ²   là bình phương của hiệu x – tọa độ của A và B và luôn dương.

Tương tự, (y ₂ – y ₁ ) ²  và  (z ₂ – z ₁ ) ²  bằng bình phương hiệu giữa các tọa độ y và z– tương ứng của A và B.

Để tìm hiểu thêm về hình học tọa độ và các chủ đề liên quan cũng như xem các video tương tác, hãy tải xuống BYJU’S – Ứng dụng Học tập.