Ở đây, tất cả các khái niệm liên quan đến nó như định nghĩa, ví dụ, thuộc tính, loại, v.v. đều được đề cập. Các khái niệm chính được đề cập ở đây bao gồm những điều sau đây.
Contents
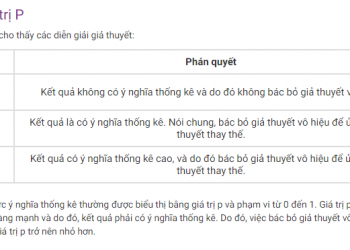
Số Lẻ là gì?
Số lẻ được định nghĩa là bất kỳ số nào không thể chia hết cho hai. Nói cách khác, một số ở dạng 2k + 1, trong đó k ∈ Z (tức là số nguyên) được gọi là số lẻ . Cần lưu ý rằng các số hoặc tập hợp các số nguyên trên một trục số có thể là số lẻ hoặc số chẵn. Một vài điểm chính khác:
- Một số lẻ là một số nguyên không phải là bội số của 2
- Nếu các số này chia hết cho 2 thì sẽ còn dư
- Trong dãy số, 1 là số lẻ dương đầu tiên
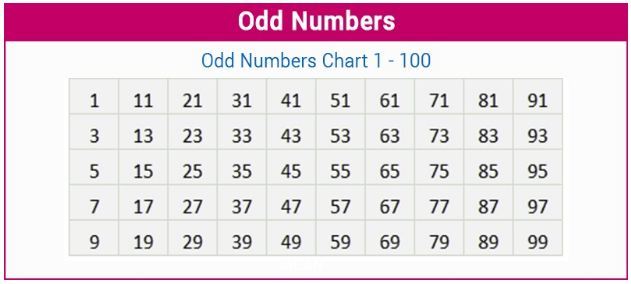
Biểu đồ số lẻ (1 đến 100)
Biểu đồ này bao gồm các số lẻ từ 1 đến 100. Bạn cũng có thể luyện viết các số lẻ từ 1 đến 1000 vào vở của mình.

Danh sách số lẻ
Có 25 số lẻ từ 1 đến 50 trong khi có 50 số từ 1 đến 100. Trong trường hợp các số từ 1 đến 1000, có 500 số lẻ và 500 số chẵn. Danh sách một số số lẻ bao gồm các số như:
- -5, -3, -1, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, v.v.
| Dãy số | Số Lẻ |
| 1 đến 50 | 25 |
| 1 đến 100 | 50 |
| 1 đến 200 | 100 |
| 1 đến 300 | 150 |
| 1 đến 500 | 250 |
| 1 đến 1000 | 500 |
| 1 đến 10000 | 5000 |
Số lẻ từ 101 đến 200
| 101 103 105 107 109 111 113 115 117 119 121 123 125 127 129 131 133 135 137 139 141 143 145 147 149 151 153 155 157 159 161 163 165 167 169 171 173 175 177 179 181 183 185 187 189 191 193 195 197 199 |
Số lẻ từ 201 đến 300
| 201 203 205 207 209 211 213 215 217 219 221 223 225 227 229 231 233 235 237 239 241 243 245 247 249 251 253 255 257 259 261 263 265 267 269 271 273 275 277 279 281 283 285 287 289 291 293 295 297 299 |
Số lẻ từ 301 đến 400
| 301 303 305 307 309 311 313 315 317 319 321 323 325 327 329 331 333 335 337 339 341 343 345 347 349 351 353 355 357 359 361 363 365 367 369 371 373 375 377 379 381 383 385 387 389 391 393 395 397 399 |
Số lẻ từ 401 đến 500
| 401 403 405 407 409 411 413 415 417 419 421 423 425 427 429 431 433 435 437 439 441 443 445 447 449 451 453 455 457 459 461 463 465 467 469 471 473 475 477 479 481 483 485 487 489 491 493 493 493 |
Tính chất
Có bốn tính chất chính của số lẻ liên quan đến phép cộng, phép trừ, phép nhân và phép chia. Mỗi thuộc tính này được thảo luận chi tiết ở các điểm sau.
Thêm hai số lẻ
Bất kỳ số lẻ nào được thêm vào một số lẻ khác luôn luôn cho một số chẵn. Tuyên bố này cũng được chứng minh dưới đây.
| Lẻ + Lẻ = Chẵn |
Bằng chứng:
Cho hai số lẻ là a và b.
Những con số này có thể được viết dưới dạng
a = 2k 1 + 1
và b = 2k 2 + 1 trong đó k 1 , k 2 ∈ Z
Thêm a + b, chúng ta có
(2k 1 + 1) + (2k 2 + 1) = 2k 1 + 2k 2 + 2 = 2 (k 1 + k 2 + 1) mà chắc chắn chia hết cho 2.
Trừ hai số lẻ
Khi một số lẻ bị trừ đi một số lẻ, kết quả sẽ luôn là một số chẵn. Điều này tương tự với việc cộng hai số lẻ, nơi người ta chứng minh rằng kết quả luôn là một số chẵn.
| Lẻ – Lẻ = Chẵn |
Phép nhân hai số lẻ
Nếu một số lẻ được nhân với một số lẻ khác, số kết quả sẽ luôn là một số lẻ. Một bằng chứng về điều này cũng được đưa ra dưới đây.
| Odd × Odd = Lẻ |
Cho hai số lẻ là a và b. Những con số này có thể được viết dưới dạng
a = 2k 1 + 1 và b = 2k 2 + 1 trong đó k 1 , k 2 ∈ Z
Bây giờ, a × b = (2k 1 + 1) (2k 2 + 1)
Vì vậy, a × b = 4k 1 k 2 + 2k 1 + 2k 2 + 1
Phương trình trên có thể được viết lại thành:
a × b = 2 (2k 1 k 2 + k 1 + k 2 ) + 1 = 2 (x) + 1
Như vậy, phép nhân hai số lẻ cho kết quả là một số lẻ.
Phân chia hai số lẻ
Phép chia hai số lẻ luôn cho kết quả là Số lẻ nếu và chỉ khi mẫu số là một thừa số của tử số, hoặc nếu không thì kết quả là số thập phân.
| Odd ⁄ Odd = Lẻ |
Nói ngắn gọn:
| Hoạt động | Kết quả |
|---|---|
| ODD + ODD | CŨNG |
| ODD – ODD | CŨNG |
| ODD x ODD | ODD |
| ODD / ODD
* mẫu số là một thừa số của tử số |
ODD |
Các loại số lẻ
Có 2 loại số lẻ chính là số lẻ liên tiếp và số lẻ ghép .
Số lẻ liên tiếp
Nếu ‘a’ là một số lẻ, thì ‘a’ và ‘a + 2’ được gọi là các số lẻ liên tiếp. Một vài ví dụ về các số lẻ liên tiếp có thể là
- 15 và 17
- 29 và 31
- 3 và 5
- 19 và 21 v.v.
Chẵn đối với các số lẻ âm, các số liên tiếp sẽ là:
- -5 và -3
- -13 và -11, v.v.
Số lẻ tổng hợp
Một số lẻ kết hợp là một số nguyên dương lẻ được tạo thành bằng cách nhân hai số nguyên dương nhỏ hơn hoặc nhân số đó với một. Các số lẻ tổng hợp có đến 100 là: 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87 , 91, 93, 95, 99.
Câu hỏi và giải pháp
Ví dụ 1: Tìm tổng của số lẻ nhỏ nhất và lớn nhất có 3 chữ số đồng thời chứng minh rằng số đó chia hết cho 2.
Giải pháp :
Số lẻ nhỏ nhất có 3 chữ số = 101
Số lẻ lớn nhất có 3 chữ số = 999
Tổng của cả hai số = 101 + 999 = 1100
Số 1100 chia hết cho 2 (theo quy tắc chia hết cho 2).
Điều này chứng tỏ rằng số lượng là số chẵn.
Ví dụ 2 : Các số sau có phải là số lẻ không?
- 25
- 15 + 13
- 32 – 37
Giải pháp :
- 25 không chia hết cho 2 nên số lẻ.
- 15 + 13 = 28, chia hết cho 2, không phải là số lẻ
- 32 – 37 = -5, là một số lẻ
Ví dụ 3: Điền vào chỗ trống:
__, 2, __, 4, __, 6, __, 8, __, 10, __, 12
22, __, 24, __, 26, __, 28, __, 30
100, __, 102, __, 104, __, 106, __, 108
Bài giải:
1,2,3,4,5,6,7,8,9,10,11,12
22,23,24,25,26,27,28,29,30
100,101,102,103,104,105,106,107,108
Ví dụ 4: Từ 1 đến 100 có bao nhiêu số lẻ?
Bài giải: Có 50 số lẻ và 50 số chẵn từ 1 đến 100.
Số các số lẻ = 100/2 = 50
Bảng tính
- 7 chẵn hay lẻ?
- Làm thế nào để bạn xác định xem một số là lẻ hay chẵn?
- Đề cập đến tất cả các số lẻ lớn hơn 60 và nhỏ hơn 120.
- Liệt kê tất cả các số lẻ lớn hơn -4 và nhỏ hơn 20.
- Số 0 có phải là số lẻ không? Tại sao?
Câu hỏi thường gặp về số lẻ
Tất cả các số lẻ là gì?
Các số không chia hết cho 2 được gọi là số lẻ. Ví dụ: 3, 5, 17, 19, 21, v.v.
Làm thế nào để bạn xác định xem một số là lẻ hay chẵn?
Nếu một số chia hết cho 2 thì đó là số chẵn, ngược lại, đó là số lẻ. Ta cũng có thể nói khi chia một số cho 2 và còn dư một số không chia hết cho 2 thì đó là một số lẻ.
Đối với một số lớn hơn là mười nghìn hoặc hàng triệu, hãy kiểm tra số ở vị trí hàng đơn vị. Nếu vị trí đơn vị mang một số chẵn, điều đó có nghĩa là toàn bộ số chẵn khác nó là một số lẻ.
Số 0 có phải là số lẻ không? Tại sao?
Không, số 0 không phải là số lẻ mà là số chẵn, bởi vì, khi chúng ta chia 0 cho 2, nó cho chúng ta một thương bằng 0 và cũng không có phần dư còn lại sau khi chia. Vì vậy, 0 chia đều cho 2.
0 ÷ 2 = 0
37 là số lẻ hay số chẵn?
Như chúng ta có thể thấy, hàng đơn vị của 37 bao gồm một số lẻ tức là 7, không chia hết cho 2, do đó, nó là một số lẻ.