Số nguyên tố & tổng hợp – Giải thích với các ví dụ

Một số nguyên tố là gì?

Số nguyên tố là số nguyên dương lớn hơn 1 và chỉ chia hết cho 1 hoặc chính nó, không có dư. Nói cách khác, một số nguyên tố là một số nguyên dương có hai thừa số dương, bao gồm 1 và chính nó. Ví dụ, 5 chỉ có thể chia cho 1 và 5.

Sự thật 

• 2 là số nguyên tố chẵn duy nhất. Tất cả các số chẵn khác đều chia hết cho 2.
• Tất cả các số nguyên tố, ngoại trừ 2, đều là số lẻ và được gọi là số nguyên tố lẻ.
• Không có số nguyên tố nào vượt quá 5 có chữ số tận cùng là 5. Tất cả các số lớn hơn 5 mà kết thúc bằng 5 đều chia hết cho 5.
• 0 và 1 không phải là số nguyên tố.

Danh sách các số nguyên tố

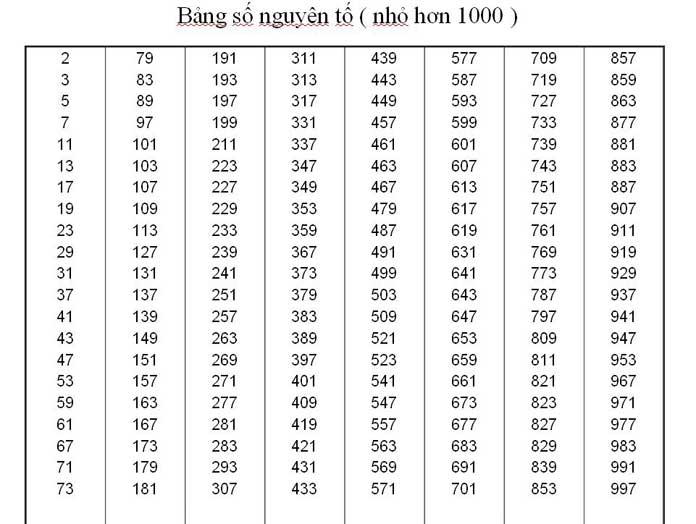
Bảng sau đây cho thấy tất cả các số nguyên tố từ 0 đến 1000:

Số tổng hợp là gì?

Trong khi số nguyên tố là số có hai thừa số, số tổng hợp là số nguyên dương hoặc số nguyên có nhiều hơn hai ước. Ví dụ, 23 chỉ có hai thừa số, 1 và 23 (1 × 23), và do đó là một số nguyên tố. Tuy nhiên, số 4 có ba ước: 1,2 và 4 (1 × 4 và 2 × 2).

Xem thêm:

Danh sách các số tổng hợp

Dưới đây là danh sách tất cả các số tổng hợp có đến 300.

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140, 141, 142, 143, 144, 145, 146, 147, 148, 150, 152, 153, 154, 155, 156, 158, 159, 160, 161, 162, 164, 165, 166, 168, 169, 170, 171, 172, 174, 175, 176, 177, 178, 180, 182, 183, 184, 185, 186, 187, 188, 189, 190, 192, 194, 195, 196, 198, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 224, 225, 226, 228, 230, 231, 232, 234, 235, 236, 237, 238, 240,242, 243, 244, 245, 246, 247, 248, 249, 250, 252, 253, 254, 255, 256, 258, 259, 260, 261, 262, 264, 265, 266, 267, 268, 270, 272, 273, 274, 275, 276, 278, 279, 280, 282, 284, 285, 286, 287, 288, 289, 290, 291, 292, 294, 295, 296, 297, 298, 299, 300.

Làm thế nào để xác định các số nguyên tố và hỗn hợp?

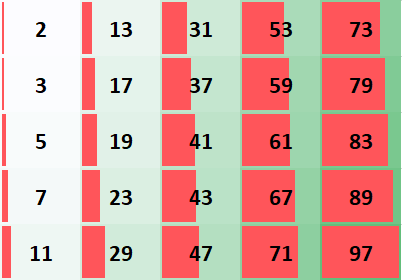
Để kiểm tra xem một số là số nguyên tố hay hợp số, phép thử chia hết của thứ tự 2, 5, 3, 11, 7 và 13 được thực hiện. Một hợp số chia hết cho bất kỳ thừa số nào ở trên. Số nhỏ hơn số 121 không chia hết cho 2, 3, 5 hoặc 7 là số nguyên tố. Nếu không, số là hỗn hợp. Một số nhỏ hơn 289, không chia hết cho 2, 3, 5, 7, 11 hoặc 13, cũng là số nguyên tố. Nếu không, số là hỗn hợp.

ví dụ 1

Xác định các số nguyên tố và hợp số từ danh sách sau.

185, 253, 253 và 263.

Giải pháp

Thực hiện phép thử chia hết để xác định hợp số và số nguyên tố.

263 là một số nguyên tố. 263 kết thúc bằng số lẻ 3 và do đó, nó không chia hết cho 2. Vì, chữ số tận cùng của nó không phải là 0 hoặc 5, số đó cũng không chia hết cho 5. Cuối cùng, căn số của 263 là 2, tức là

(2 + 6 + 3) = 11 và (1 + 1) = 2 nên không chia hết cho 3.

Số 185 có chữ số tận cùng là 5 nên 185 chia hết cho 5. Trong trường hợp này, số là hợp số.

Số 253 có chữ số tận cùng là 3 là số lẻ. Tương tự, nó không kết thúc bằng 0 hoặc 5, và do đó 253 không chia hết cho 5. Căn số của 253 được tính là (2 + 5 + 3) = 10. (1 + 0) = 1, isn ‘ t chia hết cho 3. Do đó, 253 là hợp số.

Số 243 có chữ số tận cùng là 3, vì vậy nó không chia hết cho 2. Số không có chữ số cuối cùng là 0 hoặc 5 và do đó, không chia hết cho 5. Căn số của nó nhận được là (2 + 4 + 3) = 9 chia hết cho 3. Do đó 243 là hợp số.

Xem thêm:

Sieve of Eratosthenes là gì và các thuật toán thường gặp

Số lẻ và số chẵn – Tổng quan về số chẵn và số lẻ

Ví dụ 2

Số nào sau đây là hợp số hay số nguyên tố?

3, 9, 11 và 14

Giải pháp

Số 3 là số nguyên tố vì thừa số của nó chỉ là 1 và 3. Số 9 là hợp số vì thừa số của nó là 1, 3 và 9. Số 14 là hợp số vì nó chia hết cho 1, 2, 7 và 14. Số 11 cũng là số nguyên tố vì nó chỉ có hai thừa số: 1 và 11

Ví dụ 3

Xác định các số nguyên tố và hợp số từ danh sách sau:

73, 65, 172 và 111

Giải pháp

Số 73 là một số nguyên tố. Chữ số cuối cùng không phải là 0 hoặc 5, và nó không phải là bội số của 7. Số 65 là một số hợp bởi vì chữ số cuối cùng tận cùng bằng 5 và chia hết cho 5. Căn số của số 111 là 3, và như vậy chia hết cho 3. Số 111 là hợp số. Số 172 cũng là một hợp số vì nó là số chẵn và do đó chia hết cho 2.

Ví dụ 4

Số nào sau đây là số nguyên tố hoặc hợp số?

23, 91, 51 và 113

Giải pháp

Số 23 là số nguyên tố vì các trường hợp sau: 23 không phải là số chẵn, căn số của nó là 5 và bản thân số đó không phải là bội số của 7. Căn số của 51 là 6 là bội số của 3. Số 51 như vậy là tổng hợp.

Số 91 là hợp số vì căn số là bội số của 7. Số 113 là số lẻ và không kết thúc bằng 0 hoặc 5. Căn số của 113 không chia hết cho 3 hoặc 2. Vì vậy, số 113 là số nguyên tố.

Ví dụ 5

Phân biệt số nguyên tố và hợp số trong danh sách dưới đây.

169, 143, 283 và 187

Giải pháp

Số 143 chia hết cho 11 và do đó, nó là hợp số. Số 169 cũng là hợp số vì nó chia hết cho 13. Số 187 chia hết cho 11. Trong trường hợp này, số là hợp số. Số 283 là số nguyên tố vì chữ số cuối cùng không phải là 5 hoặc 0, và căn số là 4, không chia hết cho 2, 3 hoặc 5. Nó cũng không phải là bội số của mười một, tức là (+2 – 8 + 3 ) = 3.