Diện tích tam giác – Giải thích và ví dụ chi tiết dễ hiểu nhất
3 Tháng Ba, 2021Trong bài này, chúng ta sẽ cùng nhau tìm hiểu diện tích hình tam giác là gì và cách xác định diện...
Bây giờ khi chúng ta hoàn thành với các tam giác đồng dư, chúng ta có thể chuyển sang một loại khái niệm tương tự khác , được gọi là tam giác đồng dạng.
Trong bài này, chúng ta sẽ cùng nhau tìm hiểu về tam giác đồng dạng, các đặc điểm của tam giác đồng dạng, cách sử dụng các định đề và định lý để nhận biết tam giác đồng dạng và cuối cùng là cách giải các bài toán về tam giác đồng dạng.
Contents
Khái niệm tam giác đồng dạng và tam giác đồng dạng là hai thuật ngữ khác nhau nhưng có quan hệ mật thiết với nhau. Tam giác đồng dạng là hai hay nhiều tam giác có cùng hình dạng, cặp góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau.
Hình minh họa các tam giác đồng dạng:
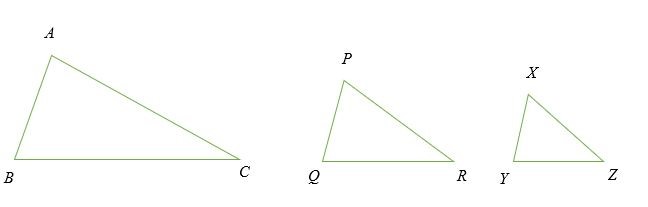

Hãy xem xét ba hình tam giác dưới đây. nếu:
AB / PQ = AC / PR = BC = QR, AB / XY = AC / XZ = BC / YZ
Do đó, ΔABC ~ ΔPQR ~ ΔXYZ
| Đặc trưng | Tam giác đồng dư | Tam giác tương tự |
| Hình dáng và kích thước | cùng kích thước và hình dạng | Hình dạng giống nhau nhưng kích thước khác nhau |
| Biểu tượng | ≅ | ~ |
| Độ dài cạnh tương ứng | Tỉ số các cạnh tương ứng trong tam giác đồng dư luôn bằng một số 1 không đổi. | Tỷ lệ của tất cả các cạnh tương ứng trong các tam giác đồng dạng là nhất quán. |
| Góc tương ứng | Tất cả các góc tương ứng đều bằng nhau | Mỗi cặp góc tương ứng bằng nhau. |
Chúng ta có thể chứng minh sự đồng dạng trong các tam giác bằng cách áp dụng các định lý tam giác đồng dạng. Đây là các định đề hoặc các quy tắc được sử dụng để kiểm tra các tam giác đồng dạng.
Có ba quy tắc để kiểm tra các tam giác đồng dạng và chúng bao gồm: quy tắc AA, quy tắc SAS hoặc quy tắc SSS.
Quy tắc Angle-Angle (AA):
Với quy tắc AA, hai tam giác được cho là đồng dạng nếu hai góc trong một tam giác cụ thể bằng hai góc của tam giác khác.
Quy tắc cạnh góc (SAS): Quy tắc
SAS cho biết rằng, hai tam giác đồng dạng nếu tỉ số hai cạnh tương ứng của chúng bằng nhau và đồng thời, góc tạo bởi hai cạnh đó cũng bằng nhau.
Quy tắc cạnh bên (SSS):
Hai tam giác đồng dạng nếu tất cả ba cạnh tương ứng của các tam giác đã cho theo cùng một tỷ lệ.
Có hai dạng bài toán tam giác đồng dạng ; đây là những bài toán yêu cầu bạn chứng minh xem một bộ tam giác đã cho có đồng dạng hay không và những bài toán yêu cầu bạn tính các góc còn thiếu và độ dài các cạnh của các tam giác đồng dạng.
Hãy xem các ví dụ sau:
ví dụ 1
Kiểm tra xem các tam giác sau có đồng dạng không
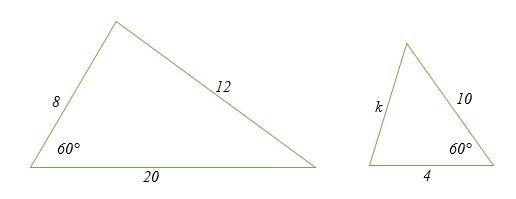

Giải pháp
Tổng các góc trong trong một tam giác = 180 °
Do đó, bằng cách xem xét Δ PQR
∠P + ∠Q + ∠R = 180 °
60 ° + 70 ° + ∠R = 180 °
130 ° + ∠R = 180 °
Trừ cả hai bên đi 130 °.
∠ R = 50 °
Xem xét Δ XYZ
∠X + ∠Y + ∠Z = 180 °
∠60 ° + ∠Y + ∠50 ° = 180 °
∠ 110 ° + ∠Y = 180 °
Trừ cả hai bên đi 110 °
∠ Y = 70 °
Vì thế;
Ví dụ 2
Tìm giá trị của x trong các tam giác sau nếu ΔWXY ~ ΔPOR.
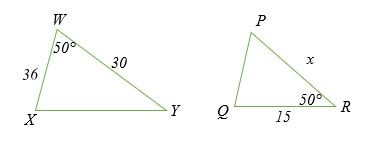

Giải pháp
Cho rằng hai tam giác đồng dạng, thì;
WY / QR = WX / PR
30/15 = 36 / x
Nhân chéo
30x = 15 * 36
Chia cả hai bên cho 30.
x = (15 * 36) / 30
x = 18
Do đó, PR = 18
Hãy kiểm tra xem tỉ lệ hai cạnh tương ứng của các tam giác có bằng nhau không.
WY / QR = WX / PR
30/15 = 36/18
2 = 2 (RHS = LHS)
Ví dụ 3
Kiểm tra xem hai tam giác dưới đây có đồng dạng không và tính giá trị k.
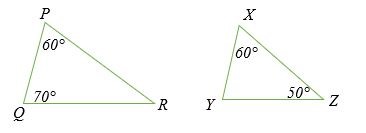

Giải pháp
Theo quy tắc Cạnh bên (SAS), hai tam giác đồng dạng.
Chứng minh:
8/4 = 20/10 (LHS = RHS)
2 = 2
Bây giờ hãy tính giá trị của k
12 / k = 8/4
12 / k = 2
Nhân cả hai vế với k.
12 = 2 nghìn
Chia cả hai bên cho 2
12/2 = 2k / 2
k = 6.
Ví dụ 4
Xem thêm:
Quy tắc sin và những quy tắc tính toán vô cùng đơn giản
Tam giác đồng dư và những ví dụ đơn giản nhất
Xác định giá trị của x trong sơ đồ sau.
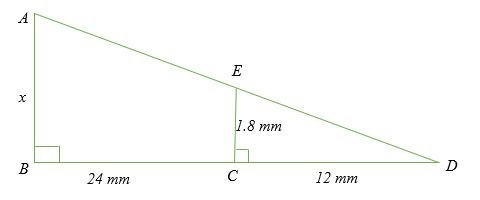

Giải pháp
Cho tam giác ABD và ECD là các tam giác đồng dạng.
Áp dụng quy tắc Side-Angle-Side (SAS), trong đó A = 90 độ.
AE / EC = BD / CD
x / 1,8 = (24 + 12) / 12
x / 1,8 = 36/12
Nhân chéo
12x = 36 * 1.8
Chia cả hai bên cho 12.
x = (36 * 1,8) / 12
= 5,4
Do đó, giá trị của x là 5,4 mm.