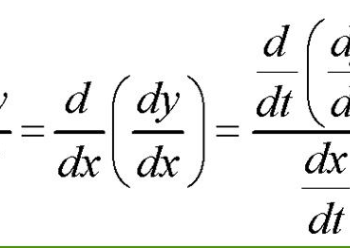Như chúng ta đã biết, vectơ là một vật thể có cả độ lớn và hướng. Để tìm độ lớn của một vectơ, chúng ta cần tính độ dài của vectơ. Các đại lượng như vận tốc, độ dời, lực, động lượng, … là các đại lượng vectơ. Nhưng tốc độ, khối lượng, quãng đường, thể tích, nhiệt độ,… là những đại lượng vô hướng. Vô hướng có độ lớn duy nhất, trong khi các vectơ có cả độ lớn và hướng.
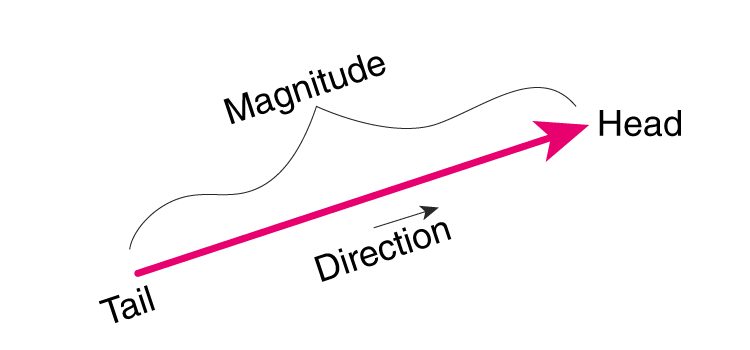

Độ lớn của công thức vectơ được sử dụng để tính độ dài của một vectơ đã cho (ví dụ v ) và được ký hiệu là | v | Vì vậy, về cơ bản, đại lượng này là độ dài giữa điểm đầu và điểm cuối của vectơ. Để tính độ lớn của vectơ, chúng ta sử dụng công thức khoảng cách , mà chúng ta sẽ thảo luận ở đây.
Tầm quan trọng của một công thức vectơ
Giả sử, AB là đại lượng vectơ vừa có độ lớn vừa có hướng. Để tính độ lớn của vectơA B→, ta phải tính khoảng cách giữa điểm đầu A và điểm cuối B. Trong mặt phẳng XY, cho A có tọa độ (x 0 , y 0 ) và B có tọa độ (x 1 , y 1 ). Do đó, theo công thức khoảng cách, độ lớn của vectơA B→, có thể được viết như;
|A B→| =(x1–x0)2+ (Y1–Y0)2––––––––––––––––√
Bây giờ nếu điểm đầu là (x, y) và điểm cuối ở gốc, thì độ lớn của công thức vectơ trở thành;
|A B→| =x2+Y2––––––√
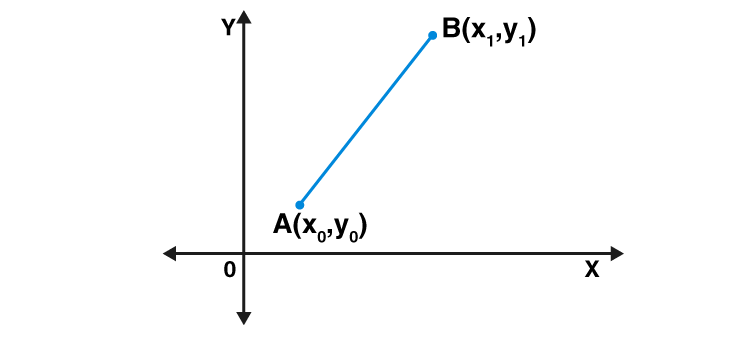
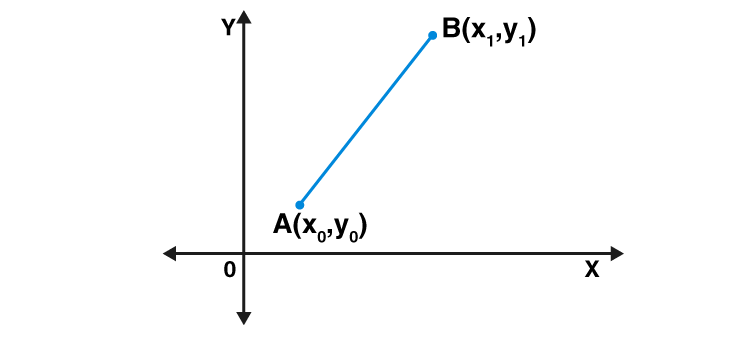
Hướng của một vectơ
Hướng của một vectơ không là gì khác ngoài số đo góc tạo với đường nằm ngang. Một trong những phương pháp để tìm hướng của vectơA B→ Là;
tan α = y / x; điểm cuối tại 0.
Trong đó x là sự thay đổi trên đường nằm ngang và y là sự thay đổi trên đường thẳng đứng.
Hoặc tan α = Y1–Y0x1–x0; trong đó (x 0, y 0 ) là điểm đầu và (x 1 , y 1 ) là điểm cuối.
Các vấn đề về tầm quan trọng của một vectơ
Bài toán 1: Tìm độ lớn của vectơA B→ có điểm đầu, A là (1, 2) và điểm cuối, B là (4, 3).
Bài giải: Cho A là (1, 2) và B là (4, 3) lần lượt là điểm đầu và điểm cuối.
Do đó, x 0 = 1 & y 0 = 2 và x 1 = 4 & y 1 = 3
Sử dụng công thức khoảng cách,
|A B→| =(x1–x0)2+ (Y1–Y0)2––––––––––––––––√
|A B→| =( 4 – 1)2+ ( 3 – 2)2–––––––––––––√
|A B→| =32+12––––––√
|A B→| =9 + 1––––√
|A B→| =10––√
|A B→| ≈ 3,2
Độ lớn của A B→ ≈ 3,2
Nếu chúng ta phải tính độ lớn của một vectơ 3d , thì sẽ có ba điểm tọa độ và chúng ta có thể biểu diễn độ lớn của vectơv⃗ như;
v⃗ = x i + y j + z k
|v⃗ | =x2+Y2+với2––––––––––√
Chúng ta hãy xem xét một đối tượng 3d.


Trong hình, bạn có thể thấy độ lớn của vectơ được biểu diễn bằng vectơ V⃗ (đường màu xanh lam), là độ dài của mũi tên biểu thị V⃗ . Vì vậy, độ dài của OP là độ lớn củaV⃗ . Để tính độ lớn, chúng ta phải sử dụng định lý Pythagoras ở đây, cho các tam giác, OBP và OAB.
Trong tam giác OBP (1)
OP 2 = OB 2 + BP 2
Và trong tam giác OAB (2)
OB 2 = OA 2 + AB 2
Từ phương trình 1 và 2, chúng ta nhận được,
OP 2 = OA 2 + AB 2 + BP 2
O P→=OA2+ AB2+ BP2–––––––––––––––√Do đó, độ lớn của vectơ 3d xi + yj + zk = x2+Y2+với2––––––––––√
Bài toán 2 Tìm độ lớn của vectơ 3d 2 i + 3 j + 4 k .
Giải: Chúng ta biết, độ lớn của vectơ 3d x i + y j + z k =x2+Y2+với2––––––––––√
Do đó, độ lớn của vectơ 3d 2 i + 3 j + 4 k =22+32+42––––––––––√
= 4 + 9 + 16––––––––√
= 29––√
Do đó, độ lớn của vectơ 3d 2 i + 3 j + 4 k ≈ 5,38