Khám phá các thành phần Vector quan trọng nhất hiện nay

Thành phần Vector – Giải thích và Ví dụ

Trong hình học vectơ, các thành phần vectơ là một trong những khái niệm quan trọng và quan trọng nhất. Toàn bộ nền tảng của hình học vectơ được thiết lập trên các thành phần vectơ.

Các thành phần vectơ được định nghĩa là:

“Việc tách một vectơ có góc thành hai vectơ hướng về các trục tọa độ trong một hệ tọa độ hai chiều được định nghĩa là các thành phần vectơ.”

Chúng tôi sẽ đề cập đến các khái niệm sau trong Thành phần Vector:

• Các thành phần của một vectơ là gì?
• Làm thế nào để tìm các thành phần của một vectơ?
• Công thức cho các thành phần vectơ là gì?
• Các ví dụ
• Câu hỏi thực hành

Các thành phần của một vectơ là gì?

Việc tách một vectơ thành 2 thành phần tương ứng của nó được định hướng dọc theo các trục tương ứng được gọi là các thành phần vectơ. Quá trình này được gọi là ‘độ phân giải của một vectơ hoặc vectơ trong một mặt phẳng.’ 

Giả sử một vectơ AB tồn tại trong hệ tọa độ hai chiều với các trục x và y. Nếu vectơ này không thẳng hàng hoàn toàn với các trục tọa độ thì vectơ AB phải ở một góc nào đó so với các trục tọa độ.

Để tìm hướng và độ lớn của một vectơ vuông góc trong một mặt phẳng hai chiều, vectơ AB được tách thành 2 thành phần tương ứng. Hai thành phần kết quả được căn chỉnh theo trục x và y.

Hai thành phần mà véc tơ (giả sử AB ) được phân giải là hướng theo phương ngang và phương thẳng đứng. Sau khi chia vectơ AB thành các thành phần của nó, có thể kết luận rằng vectơ AB là kết quả của 2 thành phần của nó, mỗi thành phần hướng theo một trục.

Lý thuyết này có thể được chứng minh bằng cách áp dụng quy tắc đầu-đuôi . Xét một vectơ AB trong không gian hai chiều. Ta có thể phân tích hai thành phần là AC và BC như hình bên:

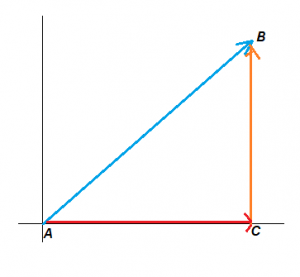
Bằng cách áp dụng quy tắc đầu-đuôi, chúng ta có thể quan sát rằng phần đuôi của AC trùng với phần đuôi của véctơ AB, và phần đầu của véctơ BC trùng với phần đầu của véctơ AB , do đó kết luận véctơ AB là kết quả của nó hai thành phần vectơ.

Về mặt toán học, nó có thể được biểu thị như sau:

AB = AC + BC

Hoặc là

| AB | = | AC | + | BC | 

Hãy xem xét một ví dụ thực tế.

Giả sử một máy bay đang bay từ Ba Lan đến Đức theo hướng tây nam. Vectơ biểu diễn mặt phẳng này có thể được chia thành hai thành phần vectơ; một hướng về phía nam, và hướng kia về phía tây. Do đó, vectơ góc hướng về phía tây nam là kết quả của hai thành phần vectơ của nó.

Một điều cần lưu ý là các thành phần của vectơ không phải là vectơ thực tồn tại trong không gian hai chiều. Chúng hầu như chỉ hiện diện với mục đích duy nhất là đơn giản hóa việc phân tích vectơ.

Việc phân giải một vectơ thành các thành phần vectơ tương ứng của nó giúp đơn giản hóa việc tính toán hình học vectơ và có thể được thực hiện trên các bài toán thực tế.

Khi chúng ta coi vectơ nằm trong một mặt phẳng hai chiều, nó chỉ có thể được phân giải thành hai thành phần, tức là X và Y, nhưng khi một vectơ là ba chiều, nó có ba thành phần có tên là X, Y và Z tương ứng. sang trục x, y và z.

Làm thế nào để tìm các thành phần của một vectơ?

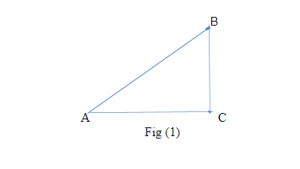
Hai thành phần của bất kỳ vectơ nào có thể được tìm thấy thông qua phương pháp phân giải vectơ. Xét vectơ như hình dưới đây, tồn tại trong một mặt phẳng hai chiều.

Vectơ AB này hợp với trục x một góc 𝛳 . Để tìm các thành phần của vectơ AB , hãy làm theo quy trình sau:

1. Thả vuông góc với trục x sao cho nó trùng với đầu của vectơ AB. 
2. Ghi nhãn nó là BC. 
3. Tương tự, kẻ một đường thẳng song song từ đuôi của vectơ AB sao cho đầu của nó trùng với đuôi của vectơ thành phần BC .
4. Gắn nhãn nó là AC.
5. Các đường thẳng BC và AC sẽ là véctơ thành phần của véctơ AB.

Hai thành phần này tạo thành một tam giác vuông cân. Các thành phần này sau đó được sử dụng để tìm độ lớn và hướng của vectơ kết quả, là AB.

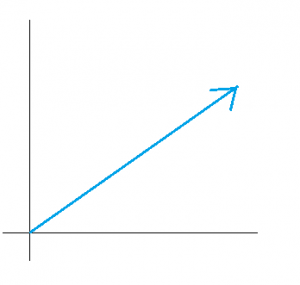
Hãy xem xét một vector v. Hai thành phần của nó trực tiếp dọc theo x và trục y sẽ là v x và vy , tương ứng. Để tìm độ lớn và hướng của vectơ v, trước tiên chúng ta cần tìm độ lớn và hướng của các thành phần vectơ của nó.

Đối với điều này, chúng tôi làm theo công thức thành phần vectơ.

Công thức thành phần vectơ là gì?

Công thức tìm thành phần của véc tơ khá đơn giản và được sử dụng rộng rãi để giải các bài toán Toán và Vật lý.

Như chúng ta đã đề cập trước đó, hai thành phần vectơ của vectơ v là v x và v y. Để  giải quyết hoàn toàn vectơ v về độ lớn và hướng, trước tiên chúng ta cần tính toán các thành phần này.

Tìm tầm quan trọng của các thành phần vectơ

Sau đây là công thức tính độ lớn của hai véc tơ thành phần:

Đối với v x :

v x = v.cos θ

Đối với v y :

v y = v.sin θ

Bằng cách làm theo các công thức này, chúng ta sẽ nhận được độ lớn của hai thành phần vectơ.

ví dụ 1

Tính và giải vectơ lực thành thành phần của nó tại đó Lực có độ lớn 10N và nghiêng một góc 30º  trong mặt phẳng đã cho như hình dưới đây:

Giải pháp

Cho rằng độ lớn của lực là 10N trong đó θ là 30º

Phân giải vectơ thành các thành phần của nó, thành phần x dọc theo trục x và thành phần y dọc theo trục y sao cho phần đầu của thành phần x trùng với phần đuôi của thành phần thứ hai theo quy tắc head-to-tail như trong hình bên dưới:

Để tìm ra độ lớn của các thành phần, chúng tôi sẽ sử dụng các công thức được nêu dưới đây:

F X = F.cos θ   eq (1)

F y = F.sin θ       eq (2)

trong đó, F = 10N, θ = 30º

đặt các giá trị trong eq (1) và eq (2),

F X = 1,545N

F y = -9.881N

Vì vậy, vectơ đã cho được phân giải thành các thành phần x và y của nó

Tìm tầm quan trọng của vectơ thông qua các thành phần

Bây giờ chúng ta đã tính được độ lớn của các thành phần vectơ, bước tiếp theo là tính độ lớn của vectơ v.

Về cơ bản, độ lớn của vectơ v là khoảng cách giữa điểm ban đầu và điểm cuối cùng. Ký hiệu độ lớn của vectơ v được định nghĩa là | v |.

Có hai cách để tính độ lớn của vectơ:

• Tính độ lớn của vectơ bằng công thức khoảng cách.
• Tính độ lớn của vectơ bằng cách sử dụng độ phân giải của các thành phần vectơ.

Sử dụng công thức khoảng cách

Nếu cho biết tọa độ của hai điểm, điểm ban đầu và điểm cuối cùng, thì công thức khoảng cách có thể tính độ lớn của vectơ v .

Gọi tọa độ điểm ban đầu A là (x 1 , y 1 ) và điểm cuối cùng B là (x 2 , y 2 ). Sau đó, công thức được định nghĩa là:

| v | = √ ((x 2 – x 1 ) 2 + (y 2 -y 1 ) 2 )

Sử dụng các thành phần vectơ

Kể từ khi vector cho v được giải quyết vào x và thành phần y v x và v y, tương ứng.

Công thức sau được áp dụng để tính độ lớn của vectơ v:

| v | = √ ((v x ) ^ 2 + (v y ) ^ 2 )

Trong đó v x = vcos θ và v y = vsin θ.

Độ lớn của vectơ v được biểu thị bằng | v |, và nó sẽ là độ lớn của kết quả của hai thành phần vectơ.

Chú ý: Độ lớn của vectơ có thể được biểu diễn theo hai cách; hoặc in nghiêng v hoặc ở dạng tuyệt đối | v |.

Ví dụ 2

Tính độ lớn của vectơ v = (3,8).

Giải pháp

Như chúng ta biết rằng,

| v | = √ ((v x ) ^ 2 + (v y ) ^ 2 )

Trong đó v x = 3, v y = 8

Đưa vào công thức cho

| v | = √ ((3) ^ 2 + (8) ^ 2 )

| v | = 8.544

Ví dụ 3

Một lực lượng 12N là hành động trên một chiếc thuyền ở một góc 51 o với ngang. Giải thành các thành phần của nó và chứng minh bằng công thức rằng độ lớn của lực là 12N.

Giải pháp

Như chúng ta biết rằng,

F x = F.cos θ

F x = 12.cos51

F x = 8,91N

F y = F.sin θ

F y = 12.sin51

F y = 8,04N

Bây giờ, hãy chứng minh bằng công thức độ lớn rằng độ lớn của lực cho trong câu hỏi là 12N.

Sử dụng công thức,

| F | = √ ((F x ) ^ 2 + (F y ) ^ 2 )

| F | = √ ((8,91) ^ 2 + (8,04) ^ 2 )

| F | = 12,00N

Do đó, nó được chứng minh bằng cách sử dụng công thức rằng độ lớn của lực là 12N

Tìm hướng của vectơ thông qua các thành phần

Hướng của vectơ v là số đo góc mà nó tạo với phương nằm ngang trong mặt phẳng

Sau đây là công thức được sử dụng để tính toán hướng của vectơ kết quả.

θ = tan -1 (v y / v x )

θ = tan -1 (vsinθ / vcosθ)

Đây là góc mà vectơ kết quả tạo với hướng + x theo cách ngược chiều kim đồng hồ. Dấu hiệu của v x và v y sẽ xác định góc phần tư mà nó nằm trong đó.

Để xác định θ, chúng tôi sẽ sử dụng các quy ước sau:

1. Không phân biệt dấu hiệu, hãy tìm giá trị của tan -1 (v y / v x ) và đặt tên cho góc này là φ .
2. Nếu cả v x và v y đều dương φ = θ
3. Nếu cả hai đều âm θ = 180 º + φ
4. Nếu v x dương và v y âm θ = 360 º – φ
5. Nếu v x âm và v y dương θ = 180 º – φ

Ví dụ 4

Tìm giá trị của θ nếu v x = 15 và v y = 8,66.

Giải pháp

Như chúng ta đã biết công thức.

θ = tan -1 (v y / v x )

θ  = tan -1 (8,66 / 15)

θ = 30 º

Ví dụ 5

Tìm độ lớn và hướng của vectơ OP = (-4,6).

Giải pháp

Độ lớn của vectơ được xác định là,

| OP | = √ ((-4) ^ 2 + (6) ^ 2 )

| OP | = √ (16 + 36)

| OP | = 7.21

Hướng của vectơ đã cho là,

φ = tan -1 (6/4)

φ = 56,3 º

Vì thành phần x là âm và thành phần y là dương nên nó nằm trong góc phần tư thứ hai, và theo quy ước đã giải thích ở trên, θ được cho là,

θ = 180º  – φ

θ = 180º – 56,3º

θ = 123,7º

Xem thêm:

Hướng dẫn thực hiện phép trừ vectơ chi tiết nhất

Cách giải phương trình vectơ chuẩn theo quy định

Vấn đề thực hành:

1. Một lực 20N nghiêng một góc 67º trên bề mặt. Giải vectơ thành thành phần của nó và tính độ lớn của lực đã cho.
2. Phân giải vectơ được hiển thị trong hình bên dưới theo quy tắc từ đầu đến đuôi và gắn nhãn chúng cho phù hợp:
3. Hai lực A = (4,5) N và B = (3,7) N tác dụng tại một điểm P. Tính độ lớn của hợp lực.
4. Tìm độ lớn và hướng của các vectơ đã cho: u = (-7,6) và v = (5,9)
5. Tìm độ lớn và hướng của vectơ điểm đầu P (-3,1) và điểm cuối Q (-2, -5).

 Câu trả lời:

1. F X = -10,4N, F Y = -17,1N, R = 20N
2. Tham khảo ví dụ 1 và rút ra cho phù hợp.
3. R = 13,9N
4. | u | = 9,2, θ = 150,25 0          | v | = 10,3, θ = 60,90
5. | PQ | = 6,08, θ = 279.