Kiến thức mới nhất về Vectơ kết quả

Trong hình học vectơ, vectơ kết quả được định nghĩa là:

“Vectơ kết quả là một tổ hợp hay nói cách đơn giản hơn, có thể được định nghĩa là tổng của hai hoặc nhiều vectơ có độ lớn và hướng riêng của nó.”

Trong chủ đề này, chúng tôi sẽ đề cập đến các khái niệm sau:

• Vectơ kết quả là gì?
• Làm thế nào để tìm vectơ kết quả?
• Làm thế nào để tìm kết quả của nhiều hơn ba vectơ?
• Làm thế nào để vẽ vector kết quả?
• Công thức và phương pháp tính véc tơ kết quả là gì?
• Các ví dụ
• Câu hỏi luyện tập.

Vectơ kết quả là gì?

Một vectơ kết quả là một vectơ cho hiệu ứng tổng hợp của tất cả các vectơ. Khi chúng ta thêm hai hoặc nhiều vectơ, kết quả là vectơ kết quả.

Hãy cùng khám phá khái niệm này bằng một ví dụ đơn giản, thực tế. Giả sử có một chùm sáng với hai hộp nằm trên nó, như trong hình dưới đây:

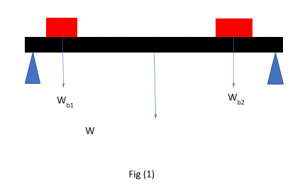
Bạn sẽ tính được trọng lượng của thanh xà và trọng lượng của hai hộp? Đúng! Bạn có thể làm quen với khái niệm vectơ kết quả.

Trong trường hợp này, vectơ kết quả sẽ là tổng các lực tác dụng lên hai hộp, tức là trọng lượng của các hộp, sẽ bằng và ngược chiều với trọng lượng của chùm. Trong trường hợp này, vectơ kết quả sẽ là tổng của hai lực vì cả hai lực đều song song và hướng theo cùng một hướng.

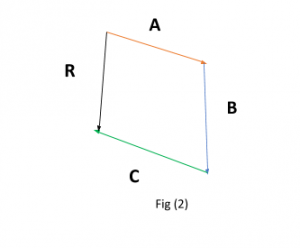
Giả sử có ba vectơ trong một mặt phẳng, vectơ A, B và C. Kết quả là R có thể được tính bằng cách cộng cả ba vectơ. Kết quả R có thể được xác định chính xác bằng cách vẽ sơ đồ cộng véc tơ được chia tỷ lệ thích hợp và chính xác được thể hiện trong hình bên dưới:

A + B + C = R

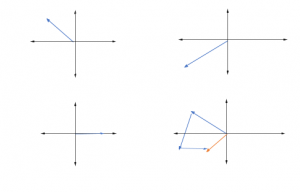
Hãy để chúng tôi hiểu rõ hơn về khái niệm này với sự trợ giúp của một ví dụ.

ví dụ 1

Tính vectơ hợp thành của ba lực song song hướng lên trên. OA = 5N, OB = 10N và OC = 15N.

Giải pháp

Như chúng ta biết rằng vectơ kết quả được cho là:

R = OA + OB + OC

 R = 5 + 10 + 15

 R = 30N

Ví dụ 2

Tìm vectơ kết quả của các vectơ đã cho OA = (3,4) và OB = (5,7).

Giải pháp

Thêm x-linh kiện để tìm R x và y thành phần để tính toán R Y .

R X = 3 + 5

R X   = 8

R y = 4 + 7

R y   = 11

Vì vậy, vectơ kết quả là R = (8,11)

Cách Tìm Vectơ Kết quả

Các vectơ có thể được thêm về mặt hình học bằng cách vẽ chúng bằng cách sử dụng một tỷ lệ chung theo quy ước đầu-đuôi , được định nghĩa là

“ Nối phần đuôi của vectơ đầu tiên với phần đầu của vectơ thứ hai, điều này sẽ tạo ra một vectơ khác có phần đầu được nối với phần đầu của vectơ thứ hai và phần đuôi của vectơ thứ nhất…”

… Đây được gọi là vectơ kết quả .

Các bước để tìm ra vectơ kết quả bằng quy tắc đầu-đuôi

Sau đây là các bước cần thực hiện để thêm hai vectơ và tìm ra vectơ kết quả:

1. Vẽ vectơ đầu tiên theo tỷ lệ đã chọn theo hướng đã cho.
2. Bây giờ nối đuôi của vectơ thứ hai với đầu của vectơ thứ nhất được vẽ theo tỷ lệ đã cho và theo hướng xác định.
3. Để vẽ vectơ kết quả, hãy nối đuôi của vectơ đầu tiên với đầu của vectơ thứ hai và đặt đầu mũi tên.
4. Để xác định độ lớn, hãy đo độ dài của kết quả R và để tìm ra hướng, hãy đo góc của kết quả với trục x.

Ví dụ 3

Hãy xem xét một thuyền buồm tàu tại 45 o về phía đông bắc. Sau đó, nó thay đổi hướng đi của nó theo hướng 165 o về phía bắc. Vẽ vectơ kết quả.

Giải pháp

Vectơ kết quả của nhiều hơn hai vectơ

Các quy tắc để tìm kết quả của một vectơ hoặc thêm nhiều hơn hai vectơ có thể được rút ngắn lại thành bất kỳ số lượng vectơ nào.

R = A + B + C + ………………………….

Giả sử có ba vectơ A, B và C , như thể hiện trong các hình dưới đây. Để thêm các vectơ này, hãy vẽ chúng theo quy tắc đầu-đuôi sao cho phần đầu của một vectơ trùng với vectơ kia. Vì vậy, vectơ kết quả được đưa ra như sau:

R = A + B + C

Lưu ý: Phép cộng vectơ có tính chất giao hoán; tổng không phụ thuộc vào thứ tự của phép cộng.

R = A + B + C = C + B + C

Tính toán vectơ kết quả bằng cách sử dụng các thành phần hình chữ nhật

Tìm một vectơ kết quả bằng cách sử dụng các thành phần của một vectơ được gọi là một phương pháp phân tích; phương pháp này mang tính toán học hơn là hình học và có thể được coi là chính xác hơn và chính xác hơn phương pháp hình học, tức là, cấu hình bằng cách sử dụng quy tắc đầu-đuôi.

Giả sử có hai vectơ A và B tạo góc θ A và θ B tương ứng với trục x dương. Các vectơ này sẽ được phân giải thành các thành phần của chúng. Chúng sẽ được sử dụng để tính toán các thành phần x và y kết quả của vectơ kết quả R, sẽ là tổng của các thành phần x và y của hai vectơ riêng biệt.

R = A + B

R X = A X + B X                       eq 1 

R Y = A Y + B Y                         phương trình 2

Kể từ, bởi các thành phần hình chữ nhật

 R = R X + R X                           eq 3

Bây giờ, đặt các giá trị của eq 1 và eq 2 trong eq 3

R = (A X + B X ) + (A Y + B Y )

Theo thành phần hình chữ nhật, độ lớn của vectơ kết quả được cho là

| R | = √ ((Rx) 2 + (Ry) 2 )

| R | = √ ((Ax + B X ) 2 + (Ay + B Y ) 2 )

Theo các thành phần hình chữ nhật, hướng của vectơ kết quả được xác định là:

θ = tan -1 (R Y / R x )

Phương pháp tương tự sẽ được áp dụng cho bất kỳ số lượng vectơ A, B, C, D …… để tìm ra vectơ kết quả R.

R = A + B + C + ……

R X = A X + B X + C X + … ..

R Y = A Y + B Y + C Y + ……

                                  R = R X + R X                                         

θ = tan -1 (R Y / R x )

Tìm vectơ kết quả bằng phương pháp hình bình hành

Theo định luật cộng vectơ hình bình hành:

 “Nếu hai vectơ tác động cùng một lúc, tại một điểm có thể được biểu diễn bằng các cạnh bên của hình bình hành được vẽ từ một điểm, thì vectơ kết quả được biểu diễn bằng đường chéo của hình bình hành đi qua điểm đó.”

Xét hai vectơ A , B tác dụng tại một điểm và được biểu diễn bởi hai cạnh của một hình bình hành như hình vẽ bên.

θ là góc giữa vectơ  A  và  B, và  R được cho là vectơ kết quả. Sau đó, theo quy định của pháp luật hình bình hành bổ sung vector, các đường chéo của hình bình hành đại diện cho kết quả của vectơ  A  và B .

Toán học Derivati trên

Dưới đây là dẫn xuất toán học:

R = A + B

Bây giờ, khai triển S thành T và vẽ QT vuông góc với OT.

Từ tam giác OTQ,

SQ 2 = OT 2 + TQ 2              eq 1,4

SQ 2 = (OS + ST) 2 + TQ 2

Trong tam giác STQ,

cosθ = ST / SQ

SQcosθ = ST

Cũng thế,

sinθ = TQ / SQ

TQ = SQsinθ

Đặt trong eq 1,4 cho,

| SQ | = √ ((A + SQsinθ) 2 + (SQcosθ) 2 )

Cho, SQ = OP = D

| SQ || = √ ((A + Dsinθ) 2 + (Dcosθ) 2 )

Giải phương trình trên cho ta,

| SQ | = √ (A 2 + 2ADcosθ + D 2 )

Vì vậy, | SQ | cho biết độ lớn của vectơ kết quả.

Bây giờ tìm ra hướng của vectơ kết quả,

tan φ = TQ / SQ

φ = tan -1 (TQ / OT)

tan φ = TQ / (OS + ST)

tan φ = Dsinθ / A + Dcosθ

φ = tan – 1 (Dsinθ / A + Dcosθ)

Chúng ta hãy hiểu rõ hơn với sự trợ giúp của một ví dụ.

Ví dụ 4

Một lực lượng 12N đang thực hiện một góc 45 o với dương trục x, và lực lượng thứ hai của 24N đang thực hiện một góc 120 o với dương trục x. Tính độ lớn của hợp lực.

Giải pháp

Bằng cách phân giải vectơ thành các thành phần hình chữ nhật của nó, chúng tôi biết rằng

R X = F 1X + F 2X

R Y = F 1Y + F 2Y

| R | = √ ((Rx) 2 + (Ry) 2 ) phương trình 1,1

Tính các giá trị của | R X | và | R Y |,

| R x | = | F 1X | + | F 2X | eq 1,2

| F 1X | = F 1 cosθ 1

| F 1X | = 12cos45

| F 1X | = 8,48N

| F 2X | = F 2 cosθ 2

| F 2X | = 24cos120

| F 2x | = -12N

Đặt các giá trị trong eq 1.2 cho,

| R x | = 8,48 + (- 12)

| R x | = -3,52N

Bây giờ, tìm thành phần y của vectơ kết quả

| R Y | = | F 1Y | + | F 2Y | eq 1.3

| F 1Y | = F 1 sinθ 1

| F 1Y | = 12sin45

| F 1Y | = 8,48N

| F 2Y | = F 2 sinθ 2

| F 2Y | = 24sin120

| F 2Y | = 20,78N

Đặt các giá trị trong eq 1.2 cho,

| R y | = 8,48 + 20,78

| R y | = 29,26N

Bây giờ, đặt các giá trị trong eq 1.1 để tính toán độ lớn của vectơ kết quả R ,

| R | = √ ((-3,52) 2 + (29,26) 2 )

| R | = √ (12,4 + 856,14)

| R | = 29,5 N

Vì vậy, độ lớn của vectơ kết quả R là 29,5N.

Ví dụ 5

Hai lực có độ lớn 5N và 10N nghiêng với nhau một góc 30 o . Tính độ lớn và hướng của vectơ kết quả bằng cách sử dụng luật hình bình hành.

Giải pháp

Cho rằng có hai lực F 1 = 5N và F 2 = 10N và một lực θ = 30 o .

Sử dụng công thức,

| R | = √ (F 1 2 + 2F 1 F 2 cosθ + F 2 2 )

| R | = √ ((5) 2 +2 (5) (10) cos30 + (10) 2 )

| R | = 14,54N

φ = tan – 1 (F 2 sinθ / F 1 + F 2 cosθ)

φ = tan -1 (10sin30 / (5 + 10cos30))

φ = 20,1 o

Vì vậy, độ lớn của vectơ kết quả R là 14,54N và hướng là 20,1 o .

Xem thêm:

Vectơ 3D và những ví dụ cụ thể nhất

Vectơ bằng nhau là như thế nào? Những nội dung cơ bản

Vấn đề thực hành

1. Tìm vectơ kết quả của các vectơ sau song song với nhau, cùng phương

1. OA = 12N, OB = 24N ( Trả lời: 36N)
2. OA = 7N, OB = 10N ( Trả lời: 17N)
3.  PQ = (3,8) RQ = (2,4) ( Trả lời: (5, 12)
4. Một lực lượng 15N đang thực hiện một góc 70 o với dương trục x, và lực lượng thứ hai của 25N đang thực hiện một góc 220 o với dương trục x. Tính độ lớn của hợp lực. ( Trả lời: 37N)
5. Tính hướng của vectơ kết quả được xác định trong bài toán số 3. ( Ans: 21,8 0 )
6. Một lực 30N tác dụng với vận tốc 25 o theo hướng đông bắc. Một lực khác 45N tác dụng ở 60 o . Tính toán và vẽ véc tơ kết quả. ( Trả lời:  22N)
7. Hai lực có độ lớn 12,7N và 35N nghiêng với nhau một góc 345 o . Tính độ lớn và hướng của vectơ kết quả bằng cách sử dụng luật hình bình hành. ( Ans: 38.3N)