Trực tâm là gì? Lý thuyết trực tâm của tam giác đầy đủ chi tiết nhất

Bài hôm nay tintuctuyensinh sẽ giới thiệu đến các bạn khái niệm trực tâm và các tính chất quan trọng trong tam giác. Để hiểu rõ hơn về chủ đề hôm nay mời các bạn cùng tham khảo bài học Trực tâm là gì? Lý thuyết trực tâm của tam giác.

1. Trực tâm là gì?

Trực tâm là giao điểm của 3 đường cao trong một tam giác.

thí dụ: Trong ảnh bên dưới, H là trực tâm của tam giác ABC.

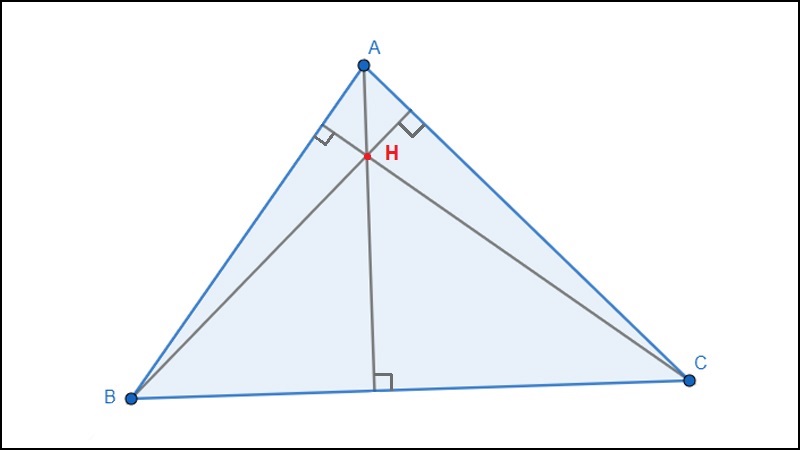
H là trực tâm của tam giác ABC

2. Cách xác định trực tâm của 1 số hình trạng học

Đối với mỗi loại tam giác sẽ có địa điểm và cách xác định trực tâm khác nhau:

– Tam giác nhọn

Trực tâm nằm ở miền trong tam giác đó.

tỉ dụ: Tam giác nhọn ABC có trực tâm H nằm ở miền trong tam giác.

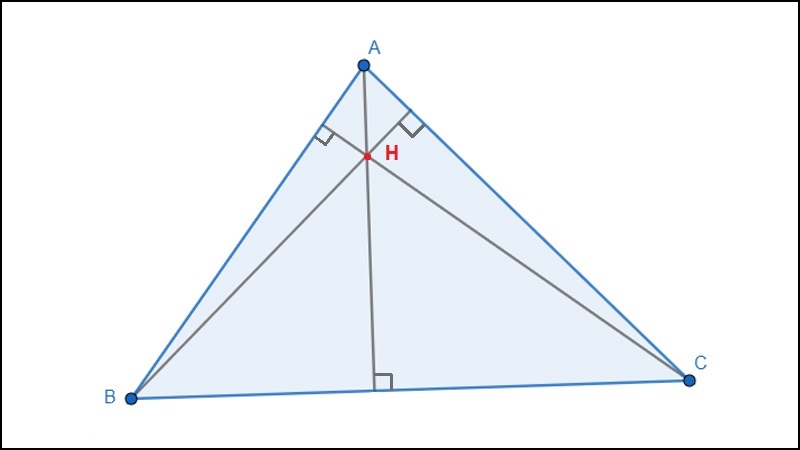
Trực tâm tam giác nhọn nằm ở miền trong tam giác

– Tam giác vuông

Trực tâm chình là đỉnh góc vuông.

tỉ dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông E.

​​

Trực tâm tam giác vuông trùng với góc vuông

– Tam giác phạm nhân

Trực tâm nằm ở miền ngoài tam giác đó.

ví dụ: Tam giác tội nhân BCD có trực tâm H nằm ở miền ngoài tam giác.

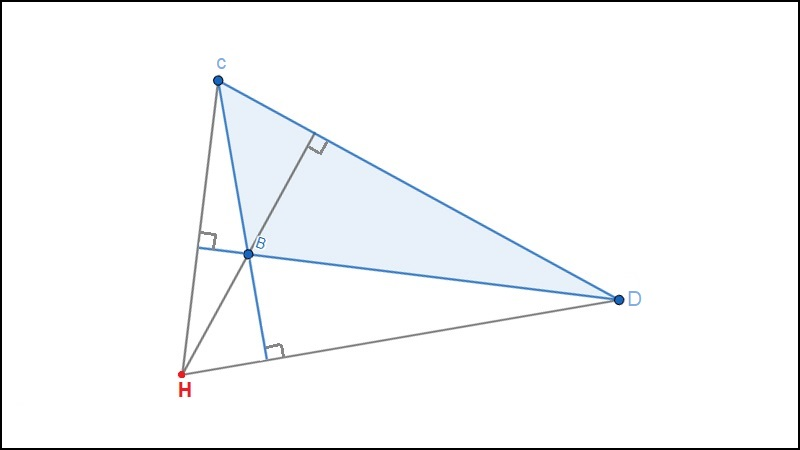
Trực tâm tam giác tầy nằm ở miền ngoài tam giác đó

1. Lý thuyết trực tâm của tam giác

Trực tâm là gì?

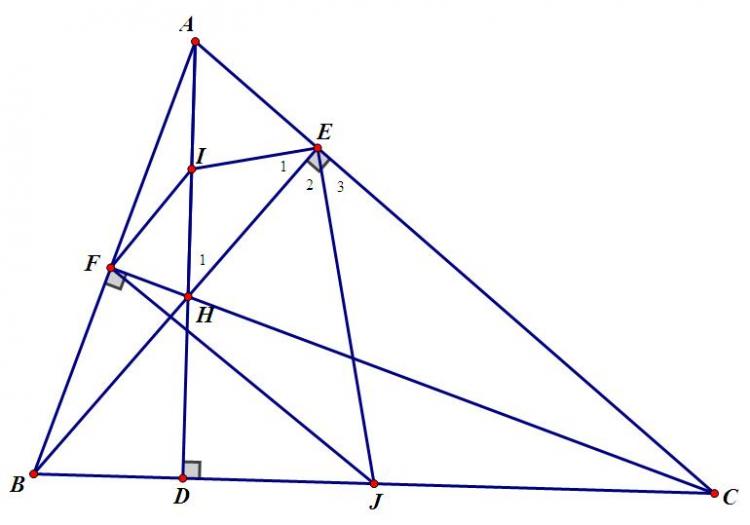
Khi vẽ ba đường thẳng xuất phát từ 3 đỉnh của một tam tam giác và vuông góc với cạnh đối diện sẽ cắt nhau tại một điểm gọi là trực tâm. Vậy ba đường đó là được gọi là đường cao trong tam giác, và giao điểm của ba đường cao đó chính là trực tâm của tam giác.

Trực tâm của tam giác sẽ tùy vào hình dáng của tam giác mà có các vị trí khác nhau, cụ thể:

+ Đối với tam giác nhọn: Trọng tâm nằm trong vùng nằm trong tam giác đó

+ Đối với tam giác vuông: Trực tâm chính là đỉnh của góc vuông

+ Đối với tam giác tù: Trực tâm sẽ nằm ngoài tam giác.

Các tính chất của trực tâm trong tam giác

Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đến trung điểm của cạnh nối hai đỉnh đối diện còn lại bằng 1/2 khoảng cách từ một đỉnh đến trực tâm tam giác đó.

Đỉnh góc vuông của tam giác vuông chính là trực tâm của tam giác đó

Nếu tam giác đó là tam giác cân thì đường cao cũng là trung tuyến, đường phân giác và đường trung trực của tam giác đó

Trong một tam giác đều, tâm đồng thời là tâm đường tròn, tâm đường tròn nội tiếp tam giác.

Trọng tâm của tam giác vuông là trung điểm của cạnh huyền

Với một tam giác đều, giao của các trung tuyến cũng là giao của các đường cao, đường trung trực, đường phân giác, …

Với một tam giác cân có một đỉnh thì giao điểm của ba trung tuyến cũng nằm trên đường cao tương ứng với đỉnh đó.

Định lý Car – not: Đường cao của tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại điểm thứ hai là điểm đối xứng của trực tâm qua cạnh tương ứng trong tam giác đó

2. Một số dạng toán thường gặp

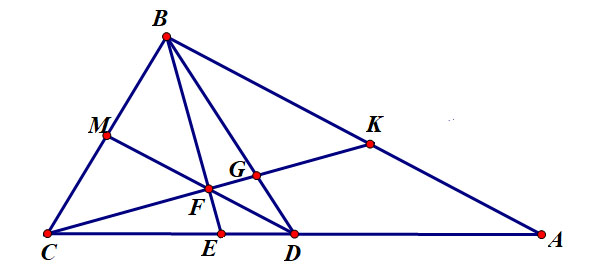
Trọng tâm là kiến ​​thức có thể áp dụng cho nhiều chủ đề toán khác nhau. Số lượng bài tập được đưa ra cũng rất nhiều và đa dạng. Để tiện cho việc học và ôn tập, chúng tôi sẽ chia các bài toán thường gặp thành các dạng sau:

Dạng số 1: Chứng minh một biểu thức đã cho sẵn

Dạng sô 2: Tính các hệ số còn ẩn chưa biết như cạnh, góc, diện tích, tỉ số, …

3. Chứng minh trực tâm của tam giác

Cho tam giác ABC, điểm D thuộc đường thẳng BC thỏa mãn AD vuông góc với BC ( AD⊥BC ) thì điểmD được gọi là hình chiếu vuông góc của A trên đường thẳng BC. Điểm D được xác định như trên được gọi là chân đường cao xuất phát từ A của tam giác ABC.ABC.

Đg cao một của tam giác chính là những đg thẳng được đi qua từ đỉnh và vuông góc với cạnh đối diện của tam giác đó. Một tam giác sẽ có 3 đường cao

Ba đường cao của tam giác đồng quy tại một điểm và điểm đó được gọi là trực tâm của tam giác.

4. Bài tập liên quan đến trực tâm tam giác

Bài tập: Cho tam giác ABC có các đường cao kẻ từ A, B, C với chân đường vuông góc lần lượt là các điểm D, E, F và cắt nhau tại H; I; J lần lượt là trung điểm của AH và BC.

1. a) Chứng minh rằng:

JT ⊥ EF

1. b) Chứng minh rằng:

IE ⊥ JE

1. c) Chứng minh rằng: DA chính là tia phân giác của góc EDF.
2. d) Đề bài cho P; Q là điểm đối xứng của D qua AB và AC

   Chứng minh rằng ba điểm P; F; E; Q thẳng hàng.

Cách giải

1. a) Sử dụng đến tính chất đường trung bình trong tam giác vuông chúng ta có:

FI = 12AH = EIFJ = 12BC = EJFI = 12AH = EIFJ = 12BC = EJ

Vậy IJ chính là đường trung trực của EF (điều phải chứng minh)

1. b) ˆE1 = ˆH1 ; ˆE3 = ˆECJ ; ˆH1 = ˆECJ nên ˆH1 = ˆECJE^1 = H^1 ; E^3 = ECJ^ ; H^1 = ECJ^ nên 

H^1 = ECJ^ (Vì Cùng phụ với góc EAH)

Vậy ˆE1 = ˆE3 E^1 =E^3

ˆIEJ = ˆE1+ˆE2 = ˆE3+ˆE2 = 900 IEJ^ =E^1 + E^2 = E^3 + E^2 = 900

c)Tứ giác BFHD và ABDE nội tiếp (điều phải chứng minh)

1. d) H được gọi là giao điểm 3 phân giác của tam giác EFD, ta có

Góc PFB = BFD

Góc DFH = EFH

4 góc này cộng lại = 2 x 90 =180 => Vì vậy ta có 3 điểm P,E,F thẳng hàng

Tương tự ta có 3 điểm F, E, Q thẳng hàng.

5. Các bài tập tương tự tham khảo

Bài tập tự luyện:

Bài tập tự luyện số 1: Cho tam giác IEF có trực tâm là G. Chứng minh rằng các điểm đối xứng với điểm G đi qua các đường thẳng chứa các cạnh hoặc trung điểm của các cạnh trên đường tròn (IEF).

Bài tập tự luyện số 2: Cho tam giác IEF với các đường cao ID, EK, FH. Trực tâm là điểm H. Có DF x BH tại điểm M, DE x CH tại điểm N. chứng minh đường thẳng đi qua I và vuông góc với MN đi qua đường tròn ngoại tiếp tam giác IEF.

Bài tập tự luyện số 3: Cho tam giác ABC có H là trực tâm. P là một điểm bất kì thuộc tam giác đã cho. Gọi A1B1C1A1B1C1 là tam giác của P với tam giác ABC. Trên HA, HB, HC lấy các điểm A2,B2,C2A2,B2,C2 sao cho AA2 = 2PA1AA2 = 2PA1, BB2 = 2PB1BB2 = 2PB1, CC2 = 2PC1CC2 =2PC1. Chứng minh tam giác ABC đồng dạng với tam giác A1B1C1A2B2C2.

Xem thêm:

Chứng chỉ HSK là gì? Dùng trong đánh giá ngoại ngữ nào?

Thời gian điều chỉnh nguyện vọng đăng ký xét tuyển Đại Học 2021

Bất ngờ tỉ lệ sinh viên có việc làm sau tốt nghiệp của các trường Y – Dược trên cả nước