Xét sự biến thiên của hàm số

1. Xét sự biến thiên của hàm số

1.1. định nghĩa hàm số đồng biến, nghịch biến

Cho hàm số y=f(x) xác định trên K (là một khoảng, nửa khoảng hay đoạn).

• Hàm số đó được gọi là đồng biến (hay tăng) trên K nếu: ∀x1,x2∈K,x1<x2 thì có f(x1)<f(x2).
• Hàm số đó được gọi là nghịch biến (hay giảm) trên K nếu: ∀x1,x2∈K,x1<x2 thì có f(x1)>f(x2).

Khảo sát sự biến thiên của hàm số là xét xem hàm số đồng biến, nghịch biến hoặc có thể không đổi trên các khoảng (nửa khoảng hay đoạn) nào đó trong tập xác định của nó.

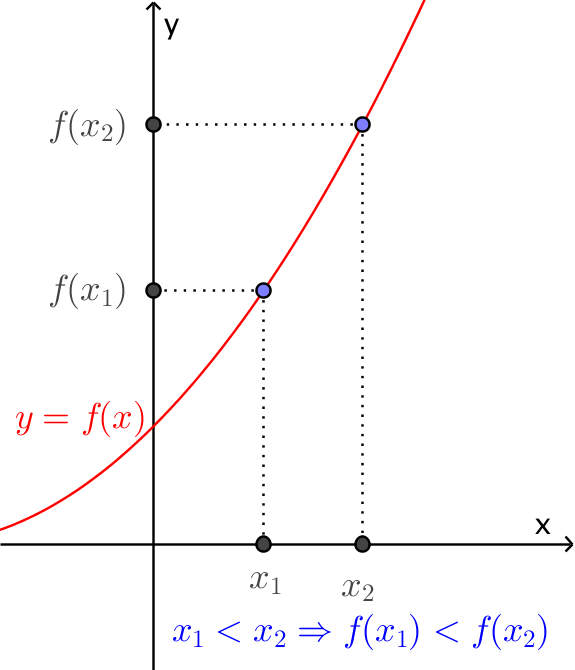
Đồ thị của hàm số đồng biến

Xét theo hướng từ trái qua phải (tức là chiều tăng của đối số x) thì:

• Đồ thị hàm số đồng biến có hướng đi lên (tăng).
• Đồ thị hàm số nghịch biến có hướng đi xuống (giảm).

Từ định nghĩa, ta có các cách xét tính đồng biến, nghịch biến của hàm số y=f(x) trên K.

1.2. Cách xét sự đồng biến nghịch biến của hàm số

Cách 1. Xét sự đồng biến nghịch biến của hàm số bằng định nghĩa. sử dụng giả định x1,x2∈K bất cứ x1<x2, bình chọn trực tiếp và so sánh f(x1) với f(x2).

tỉ dụ 1. Xét tính đồng biến, nghịch biến của hàm số y=1−2x−−−−−√ trên (−∞,12].

Ta có, ∀x1,x2∈(−∞,12],x1<x2 thì

hay hàm số nghịch biến trên (−∞,12].

Cách 2. Xét sự đồng biến nghịch biến của hàm số bằng xét dấu tỷ số biến thiên

với x1,x2∈K bất kỳ và x1≠x2.

• Nếu T>0 thì hàm số đồng biến trên K;
• Nếu T<0 thì hàm số nghịch biến trên K.

thí dụ 1. Khảo sát sự biến thiên của các hàm số y=f(x)=x+3.

chỉ dẫn.

• Tập xác định D=R.
• Với mọi x1,x2∈R và x1≠x2 ta có:
• Vậy, hàm số đồng biến trên R.

tỉ dụ 2. Khảo sát sự biến thiên của các hàm số y=f(x)=x3+2x+8.

hướng dẫn.

• Tập xác định D=R.
• Với mọi x1,x2∈R và x1≠x2 ta có:
• Vậy, hàm số đồng biến trên R.

thí dụ 3. Xét sự biến thiên của hàm số y=3x+1x−2 trên các khoảng (−∞;2) và (2;+∞).

Xét tỉ số biến thiên

Suy ra với x1,x2∈(−∞;2) hoặc x1,x2∈(2;+∞) thì T<0 nên hàm số nghịch biến trên các khoảng (−∞;2),(2;+∞).

Cũng có thể xét tính đồng biến, nghịch biến của hàm số một cách gián tiếp ưng chuẩn tính đồng biến nghịch biến của các hàm số thân thuộc hoặc đã được xét trước đó.

chả hạn ta dễ ợt có các thuộc tính sau: tổng của hai hàm số đồng biến (nghịch biến) trên K là một hàm số đồng biến (nghịch biến) trên đó; tích của nhì hàm số đồng biến và nhận giá trị dương trên K là một hàm số đồng biến trên đó…

ví dụ 4. Khảo sát sự biến thiên của hàm số y=f(x)=x2+2−−−−−√.

Sự khác biệt giữa hợp ngữ và ngôn ngữ cấp cao

Con trỏ Vs. Mảng: Tìm sự khác biệt giữa con trỏ tới một mảng và mảng con trỏ

Sự khác biệt giữa Bộ xử lý lõi kép và Bộ xử lý DUO lõi 2

Sự khác biệt giữa Vòng lặp While và Do While

hướng dẫn.

• Tập xác định D=R.
• Với x1,x2∈D và x1≠x2 ta có:
• Khi đó:
  • Nếu x1,x2> 0 thì T>0 và bởi đó hàm số đồng biến trên (0;+∞).
  • Nếu x1,x2<0 thì T<0 suy ra hàm số nghịch biến trên (−∞;0).

ví dụ 5. Khảo sát sự biến thiên của hàm số hàm số y=x3+2x+3−−−−−√ trên tập xác định của nó.

hướng dẫn. Ta có hàm số đã cho có tập xác định là D=[−32;+∞).

Các hàm số y=x3 và y=2x+3−−−−−√ đều là các hàm số đồng biến trên D nên hàm số y=x3+2x+3−−−−−√ là hàm số đồng biến trên D.

thí dụ 6. Khảo sát sự biến thiên của hàm số:

1. f(x)=x32x−3−−−−−√;
2. g(x)=x32x+3−−−−−√.

2. Các thí dụ khảo sát sự biến thiên của hàm số lớp 10

Bài 1. Xét sự biến thiên của hàm số sau trên khoảng (1;+∞)

• y=3x−1
• y=x+1x

Bài 2. Xét sự biến thiên của hàm số sau trên tập xác định của nó:

• y=3x−1−−−−−√+x−−√
• y=x3+x−−√

Bài 3. Xét tính đồng biến, nghịch biến của các hàm số sau trên khoảng được chỉ ra

• f(x)=−2×2−7 trên khoảng (−4,0) và trên khoảng (3,10);
• f(x)=xx−7 trên khoảng (−∞,7) và trên khoảng (7,+∞);
• y=−3x+2 trên R;
• y=x2+10x+9 trên khoảng (−5,+∞);
• y=−1x+1 trên khoảng (−3,−2) và (2,3).

Bài 4. Xét tính đồng biến hay nghịch biến của các hàm số trên khoảng cho trước:

• y=x−−√ trên (0;+∞);
• y=1x+2 trên (−∞;−2);
• y=x2−3x trên (2;+∞);
• y=x3+2x−1 trên (−∞;+∞);
• y=x3−3x trên (1;+∞);
• y=x2−1−−−−−√+x trên (1;+∞).

Bài 5. Xét sự biến thiên của hàm số y=xx−2 trên tập xác định của nó.

Bài 6. Xét sự biến thiên của hàm số y=∣∣x+|2x−1|∣∣ trên tập xác định của nó.