Mở rộng thập phân của số hợp lý là gì? Xem xong hiểu luôn.

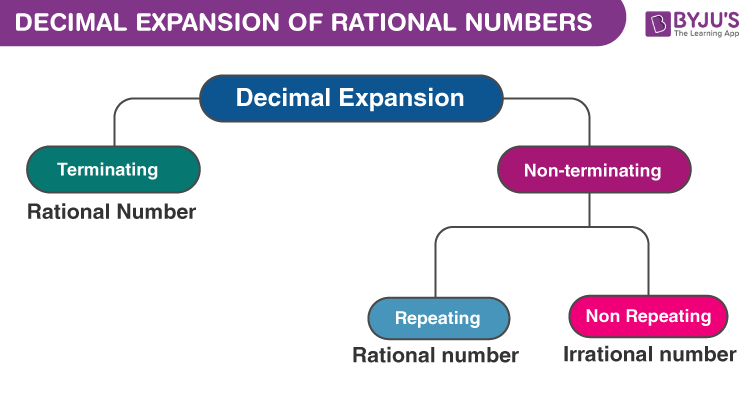
Làm thế nào để mở rộng số hợp lý trong số thập phân?

Các số thực lặp lại hoặc kết thúc về bản chất thường là các số hữu tỉ.

Ví dụ, hãy xem xét số 33.33333 ……. Nó là một số hữu tỉ vì nó có thể được biểu diễn dưới dạng 100/3 . Có thể thấy rằng phần thập phân .333 …… là phần lặp không kết thúc , tức là. nó là một số thập phân lặp lại.

Ngoài ra, các số thập phân tận cùng như 0,375, 0,6, v.v. thỏa mãn điều kiện là số hữu tỉ (0,375 = 323 ,0,6 = 35).

Xem xét bất kỳ số thập phân nào. Ví dụ: 0,567. Nó có thể được viết là 567/1000 hoặc567103. Tương tự, các số 0,6689,0.032 và .45 có thể được viết dưới dạng6689104 ,32103 và 45102 tương ứng ở dạng phân số.

Như vậy, có thể thấy rằng bất kỳ số thập phân nào cũng có thể được biểu diễn dưới dạng phân số có mẫu số theo lũy thừa là 10. Chúng ta biết rằng các thừa số nguyên tố của 10 là 2 và 5, có thể kết luận rằng bất kỳ số hữu tỉ thập phân nào cũng có thể dễ dàng biểu diễn bằng hình thức của pq, sao cho p và q là các số nguyên và thừa số nguyên tố của q có dạng 2x 5Y, trong đó x và y là các số nguyên không âm.

Tuyên bố này dẫn đến một định lý rất quan trọng.

Định lý

Định lý 1: Nếu m là bất kỳ số hữu tỉ nào mà khai triển thập phân có bản chất là tận cùng thì m có thể được biểu diễn dưới dạngpq, trong đó p và q là đồng nguyên tố và thừa số nguyên tố của q có dạng 2x 5Y, trong đó x và y là các số nguyên không âm.

Ngược lại của định lý này cũng đúng và nó có thể được phát biểu như sau:

Định lý 2: Nếu m là một số hữu tỉ, nó có thể được biểu diễn dưới dạng tỉ số của hai số nguyên tức làpq và thừa số nguyên tố của q có dạng 2x 5Y, khi đó x và y là các số nguyên không âm, thì có thể nói rằng m có khai triển thập phân là kết thúc.

Hãy xem xét các ví dụ sau:

1. 7số 8 = 723 = 7 ×  5323 × 53 = 875103
2. 380 = 324 × 5  = 3 ×  5324 × 54 = 375104

Chuyển sang khai triển thập phân của các số hữu tỉ được lặp lại, định lý sau có thể được phát biểu:

Định lý 3: Nếu m là một số hữu tỉ, nó có thể được biểu diễn dưới dạng tỉ số của hai số nguyên tức làpq và thừa số nguyên tố của q không có dạng 2x 5Y, trong đó x và y là các số nguyên không âm. Khi đó, có thể nói rằng m có một khai triển thập phân là lặp không kết thúc (định kỳ).

Hãy xem xét các ví dụ sau:

1. 16 = 0,1666 … . = 0,16¯¯¯
2. 712 = 0,58333 … = 0,583¯¯¯
3. 911 = 0,8181 … = 0.81¯¯¯¯¯

Ví dụ về số hữu tỉ thành số thập phân

Trường hợp 1: Phần dư bằng 0

Ví dụ: Tìm khai triển số thập phân của 3/6.

Ở đây, thương là 0,5 và dư là 0. Số hữu tỉ 3/6 cho kết quả là số thập phân có tận cùng.

Trường hợp 2: Phần dư không bằng 0 

Ví dụ: Biểu thị 5/13 dưới dạng số thập phân .

Ở đây, thương là 0,384615384 và phần dư không bằng 0. Lưu ý rằng số… 384 sau số thập phân đang lặp lại. Do đó, 5/13 cung cấp cho chúng ta một khai triển thập phân định kỳ không kết thúc. Và điều này có thể được viết là 5/13 =

Một số hữu tỉ cho phép khai triển thập phân định kỳ có kết thúc hoặc không kết thúc. Do đó, chúng ta có thể nói rằng một số có khai triển thập phân là kết thúc hoặc định kỳ không kết thúc là số hữu tỉ. 

Xanthogranuloma vị thành niên là gì? Những nguyên nhân, triệu chứng

Giải bất phương trình bậc hai – Giải thích & Ví dụ