Biến đổi Laplace là gì?
Một hàm được cho là một hàm liên tục theo từng phần nếu nó có số lần ngắt là hữu hạn và nó không phát nổ đến vô cùng ở bất kỳ đâu. Giả sử rằng hàm f (t) là một hàm liên tục từng phần, khi đó f (t) được xác định bằng cách sử dụng biến đổi Laplace. Biến đổi Laplace của một hàm được biểu diễn bởi L {f (t)} hoặc F (s). Phép biến đổi Laplace giúp giải các phương trình vi phân, trong đó nó rút gọn phương trình vi phân thành một bài toán đại số.
Công thức biến đổi Laplace
Biến đổi Laplace của f (t), được ký hiệu là L { f (t)} hoặc F (s) được xác định bởi công thức biến đổi Laplace:


bất cứ khi nào tích phân không đúng hội tụ.
Ký hiệu chuẩn: Khi ký hiệu rõ ràng, chúng ta sẽ sử dụng một ký tự viết hoa để chỉ ra phép biến đổi Laplace, ví dụ: L (f; s) = F (s).
Phép biến đổi Laplace mà chúng ta đã định nghĩa đôi khi được gọi là phép biến đổi Laplace một phía . Có một phiên bản hai phía mà tích phân đi từ −∞ đến ∞.
Thuộc tính của biến đổi Laplace
Một số thuộc tính của phép biến đổi Laplace là:
Nếu f 1 (t) ⟷ F 1 (s) và [lưu ý: ⟷ ngụ ý Biến đổi Laplace]
f 2 (t) ⟷ F 2 (s) thì
| Thuộc tính tuyến tính | A f 1 (t) + B f 2 (t) ⟷ AF 1 (s) + BF 2 (s) |
| Thuộc tính thay đổi tần số | e s 0 t f (t)) ⟷ F (s – s 0 ) |
| Hội nhập | t ∫ 0 f (λ) dλ ⟷ 1⁄s F (s) |
| Nhân theo thời gian | T f (t) ⟷ (−d F (s) ⁄ds) |
| Thuộc tính Shift phức tạp | f (t) e -Tại ⟷ F (s + a) |
| Thuộc tính đảo ngược thời gian | f (-t) ⟷ F (-s) |
| Thuộc tính tỷ lệ thời gian | f (t⁄a) ⟷ a F (as) |
Bảng biến đổi Laplace
Bảng biến đổi Laplace sau đây giúp giải các phương trình vi phân cho các hàm khác nhau:
| SI. Không. | f (t) | L (f (t)) = F (s) | SI. Không. | f (t) | L (f (t)) = F (s) |
|---|---|---|---|---|---|
| 1 | 1 | 1 / s | 11 | e (tại) | 1 / (s – a) |
| 2 | t n tại t = 1,2,3,… | n! / s (n + 1) | 12 | t p , ở p> -1 | Γ (p + 1) / s (p + 1) |
| 3 | √ (t) | √π / 2s (3/2) | 13 | t (n-1/2) tại n = 1,2, .. | (1.3.5… (2n-1) √π ) / (2 n s (n + 1/2) |
| 4 | tội lỗi (tại) | a / (s 2 + a 2 ) | 14 | cos (lúc) | s / (s 2 + a 2 ) |
| 5 | t sin (tại) | 2as / (s 2 + a 2 ) 2 | 15 | t cos (tại) | (s 2 -a 2 ) / (s 2 + a 2 ) 2 |
| 6 | sin (at + b) | (s sin (b) + a cos (b) / (s 2 + a 2 ) | 16 | cos (at + b) | (s cos (b) -a sin (b) / (s 2 + a 2 ) |
| 7 | sinh (at) | a / (s 2 -a 2 ) | 17 | cosh (lúc) | s / (s 2 -a 2 ) |
| số 8 | e (at) sin (bt) | b / ((sa) 2 + b 2 ) | 18 | e (at) cos (bt) | (sa) / ((sa) 2 + b 2 ) |
| 9 | e (ct) f (t) | F (sc) | 19 | t n f (t) tại n = 1,2,3 .. | (-1) n F n s |
| 10 | f ‘(t) | sF (s) – f (0) | 20 | f ”(t) | s 2 F (s) – sf (0) – f ‘(0) |
Biến đổi Laplace của phương trình vi phân
Phép biến đổi Laplace là một kỹ thuật toán học được sử dụng phổ biến để giải một phương trình vi phân. Nhiều vấn đề toán học được giải quyết bằng cách sử dụng các phép biến đổi. Ý tưởng là chuyển đổi vấn đề thành một vấn đề khác dễ giải quyết hơn. Mặt khác, phép biến đổi nghịch đảo rất hữu ích để tính toán lời giải cho bài toán đã cho.
Để hiểu rõ hơn, chúng ta hãy giải một phương trình vi phân bậc nhất với sự trợ giúp của phép biến đổi Laplace,
Xét y’- 2y = e 3x và y (0) = -5. Tìm giá trị của L (y).
Bước đầu tiên của phương trình có thể được giải với sự trợ giúp của phương trình tuyến tính:
L (y ‘- 2y] = L (e 3x )
L (y ‘) – L (2y) = 1 / (s-3)
(vì L (e ax ) = 1 / (sa))
L (y ‘) – 2s (y) = 1 / (s-3)
sL (y) – y (0) – 2L (y) = 1 / (s-3)
(Sử dụng thuộc tính tuyến tính của phép biến đổi Laplace)
L (y) (s-2) + 5 = 1 / (s-3) (Giá trị sử dụng của y (0) tức là -5 (đã cho))
L (y) (s-2) = 1 / (s-3) – 5
L (y) = (-5s + 16) / (s-2) (s-3)… .. (1)
ở đây (-5s + 16) / (s-2) (s-3) có thể được viết thành -6 / s-2 + 1 / (s-3) bằng cách sử dụng phương pháp phân số từng phần
(1) ngụ ý L (y) = -6 / (s-2) + 1 / (s-3)
L (y) = -6e 2x + e 3x
Chức năng bước
Hàm bước thường được gọi là hàm Heaviside, và nó được định nghĩa như sau:
uc( t ) = {01tôi f t < ctôi f t ≥ c
Hàm bước có thể nhận các giá trị 0 hoặc 1. Nó giống như một công tắc bật và tắt. Các ký hiệu đại diện cho các hàm Heaviside là u c (t) hoặc u (tc) hoặc H (tc)
Biến đổi Laplace song phương
Phép biến đổi Laplace cũng có thể được định nghĩa là phép biến đổi Laplace song phương. Đây còn được gọi là phép biến đổi Laplace hai mặt, có thể được thực hiện bằng cách mở rộng các giới hạn của tích phân thành toàn bộ trục thực. Do đó, phép biến đổi Laplace đơn phương phổ biến trở thành một trường hợp đặc biệt của phép biến đổi Laplace song phương, trong đó định nghĩa hàm được biến đổi được nhân với hàm bậc Heaviside.
Phép biến đổi Laplace song phương được định nghĩa là:
F( s ) =∫+ ∞– ∞e– s tf( t ) dt
Một cách khác để biểu diễn phép biến đổi Laplace song phương là B {F}, thay vì F.
Biến đổi Laplace ngược
Trong phép biến đổi Laplace ngược, chúng ta được cung cấp (các) phép biến đổi F và được yêu cầu tìm hàm số mà chúng ta có ban đầu. Biến đổi nghịch đảo của hàm F (s) được cho bởi:
f (t) = L -1 {F (s)}
Ví dụ, đối với hai phép biến đổi Laplace, chẳng hạn F (s) và G (s), phép biến đổi Laplace ngược được xác định bởi:
L -1 {aF (s) + bG (s)} = a L -1 {F (s)} + bL -1 {G (s)}
Trong đó a và b là hằng số.
Trong trường hợp này, chúng ta có thể thực hiện phép biến đổi nghịch đảo cho các phép biến đổi riêng lẻ và thêm các giá trị không đổi của chúng vào các vị trí tương ứng và thực hiện phép toán để nhận được kết quả.
Tích phân chuyển đổi
Nếu các hàm f (t) và g (t) là các hàm liên tục từng đoạn trên khoảng [0, ∞), thì tích phân chập của f (t) và g (t) được cho là:
(f * g) (t) = 0 ∫ t f (tT) g (T) dT
Như, tích phân chập tuân theo thuộc tính, (f * g) (t) = (g *) (t)
Chúng ta có thể viết, 0 ∫ t f (tT) g (T) dT = 0 ∫ t f (T) g (tT) dt
Vì vậy, dữ kiện trên sẽ giúp chúng ta nhận được phép biến đổi nghịch đảo của tích các phép biến hình.
(tức là) L (f * g) = F (s) G (s)
L -1 {F (s) G (s)} = (f * g) (t).
Biến đổi Laplace trong lý thuyết xác suất
Trong lý thuyết xác suất thuần túy và ứng dụng, phép biến đổi Laplace được định nghĩa là giá trị kỳ vọng. Nếu X là biến ngẫu nhiên có hàm mật độ xác suất, giả sử f, thì biến đổi Laplace của f được cho dưới dạng kỳ vọng của:
L {f} (S) = E [e -sX ], được gọi là phép biến đổi Laplace của chính biến ngẫu nhiên X.
Các ứng dụng của Biến đổi Laplace
- Nó được sử dụng để chuyển đổi các phương trình vi phân phức tạp sang dạng đơn giản hơn có đa thức.
- Nó được sử dụng để chuyển đổi các đạo hàm thành nhiều biến miền và sau đó chuyển đổi các đa thức trở lại phương trình vi phân bằng cách sử dụng phép biến đổi Laplace ngược.
- Nó được sử dụng trong lĩnh vực viễn thông để gửi tín hiệu đến cả hai phía của phương tiện truyền thông. Ví dụ, khi các tín hiệu được gửi qua điện thoại thì trước tiên chúng được chuyển đổi thành một sóng thay đổi theo thời gian và sau đó được chồng lên phương tiện.
- Nó cũng được sử dụng cho nhiều nhiệm vụ kỹ thuật như Phân tích mạch điện, xử lý tín hiệu kỹ thuật số, mô hình hóa hệ thống, v.v.
Ví dụ về biến đổi Laplace
Các ví dụ dưới đây dựa trên một số hàm cơ bản quan trọng của phép biến đổi Laplace.


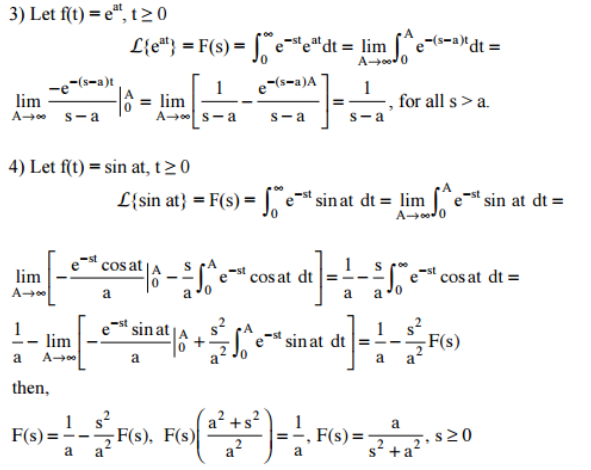
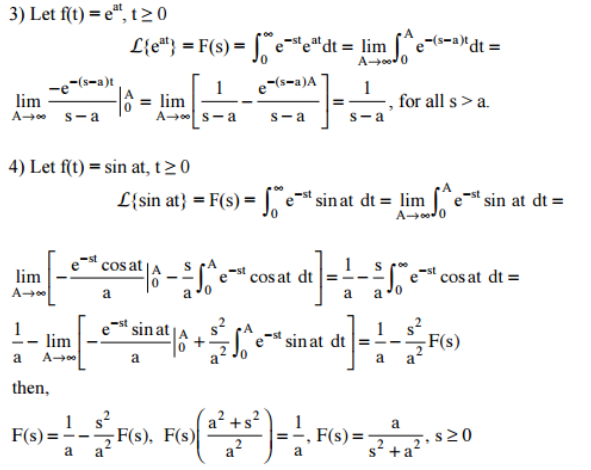
Phương trình Laplace
Phương trình Laplace, một phương trình đạo hàm riêng cấp hai, rất hữu ích trong vật lý và toán học. Phương trình Laplace phát biểu rằng tổng các đạo hàm riêng cấp hai của f, hàm chưa biết, bằng 0 đối với tọa độ Descartes. Phương trình Laplace hai chiều cho hàm f có thể được viết dưới dạng:


Phương trình Laplace cho tọa độ ba chiều có thể được biểu diễn như sau:


Câu hỏi thường gặp về Biến đổi Laplace- Câu hỏi thường gặp
Công dụng của Biến đổi Laplace là gì?
Làm thế nào để bạn tính toán biến đổi Laplace?
Bước 1: Nhân hàm số đã cho, tức là f (t) với e ^ {- st}, trong đó s là số phức sao cho s = x + iy
Bước 2; Tích hợp sản phẩm này với thời gian (t) bằng cách lấy các giới hạn là 0 và ∞.
Quá trình này dẫn đến biến đổi Laplace của f (t), và được ký hiệu là F (s).
Phương pháp Laplace là gì?
Các thuộc tính của Biến đổi Laplace là gì?
Thuộc tính tuyến tính: A f_1 (t) + B f_2 (t) ⟷ A F_1 (s) + B F_2 (s)
Thuộc tính dịch chuyển tần số: es0t f (t)) ⟷ F (s – s0 )
Thuộc tính Đạo hàm thứ n: (d ^ nf (t) / dt ^ n) ⟷ s ^ n F (s) – n∑i = 1 s ^ {n – i} f ^ {i – 1} (0 ^ -)
Tích phân: t∫_0 f (λ) dλ ⟷ 1⁄s F (s)
Phép nhân theo thời gian: T f (t) ⟷ (−d F (s) ⁄ds)
Thuộc tính Shift Complex: f (t) e ^ {- at} ⟷ F (s + a)
Thuộc tính Đảo ngược Thời gian: f (-t) ⟷ F (-s)
Thuộc tính Tỷ lệ Thời gian: f (t⁄a) ⟷ a F (as)