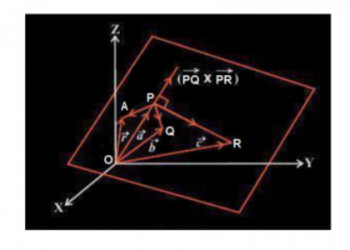
Nếu M [ij] là ma trận amxn, và chúng ta muốn tìm chuyển vị của ma trận này, chúng ta cần hoán đổi các hàng thành cột và cột thành hàng. Nó sẽ được ký hiệu là M T hoặc M ‘. Vì vậy, nếu M = [M [ij] ] mxn là ma trận ban đầu, thì M ‘= [M [ji] ] nxm là chuyển vị của nó.
Ví dụ: M = [253647]
cái M ‘= ⎡⎣⎢234567⎤⎦⎥
Trong bài viết này, chúng ta hãy thảo luận về một số thuộc tính quan trọng của ma trận chuyển vị được đưa ra với ví dụ.
Thuộc tính ma trận Transpose
Một số tính chất quan trọng của ma trận chuyển vị được đưa ra ở đây cùng với các ví dụ để giải các bài toán phức tạp.
1. Chuyển vị của ma trận là chính ma trận. [M T ] T = M
Ví dụ: M = [253647]
cái M ‘= ⎡⎣⎢234567⎤⎦⎥
và [M ‘]’ = [253647]
2. Nếu có một vô hướng a, thì chuyển vị của ma trận M nhân với vô hướng (a) bằng hằng số nhân với chuyển vị của ma trận M ‘. (AM) T = aM T .
Ví dụ:
nếu M = [253647] và hằng số a = 2, thì
LHS: [aM] T = (2[253647]) T
I E [410612số 814]T
⎡⎣⎢46số 8101214⎤⎦⎥RHS: a [M] T = 2 ([253647]) T
= 2 (⎡⎣⎢234567⎤⎦⎥)
= ⎡⎣⎢46số 8101214⎤⎦⎥
Vì vậy, LHS = RHS
3. Tổng các phép chuyển vị của ma trận bằng phép chuyển vị của tổng hai
ma trận. (M + N) T = M T + N T
M = [253647]
N = [số 8119121013]
Bằng chứng :
(M + N) T = M T + N T
LHS = ([253647] + [số 8119121013]) T
=( [2 + 85 + 113 + 96 + 124 + 107 + 13] )T
= ( [101612181420]) T
=⎡⎣⎢101214161820⎤⎦⎥
RHS = ( [253647])T+ ( [số 8119121013])T
= (⎡⎣⎢234567⎤⎦⎥) + (⎡⎣⎢số 8910111213⎤⎦⎥)
= (⎡⎣⎢2 + 83 + 94 + 105 + 116 + 127 + 13⎤⎦⎥)
=⎡⎣⎢101214161820⎤⎦⎥
LHS = RHS
4. Tích của hai ma trận theo thứ tự ngược lại bằng
chuyển vị của sản phẩm của họ. (MN) T = N T M T
Thuộc tính trên đúng với bất kỳ tích nào của bất kỳ số lượng ma trận nào.
LHS = (MN) T =(⎡⎣⎢135246⎤⎦⎥X⎡⎣⎢7911số 81012⎤⎦⎥)T
= (⎡⎣⎢1 X73 X95 X112 Xsố 84 X106 X12⎤⎦⎥) T
= (⎡⎣⎢72755164072⎤⎦⎥) T
= [71627405572]
RHS = (⎡⎣⎢7911số 81012⎤⎦⎥)TX(⎡⎣⎢135246⎤⎦⎥)T
= ( [7số 89101112] )X( [123456] )
= ([7 X18 X29 X310 X411 X512 X6])
= ([71627405572])
LHS = RHS
Xem thêm: