Hướng dẫn giải biểu thức phân chia dễ hiểu nhất hiện nay

Biểu thức phân chia – Phương pháp & Ví dụ

Biểu thức đại số là một cụm từ toán học trong đó các biến và hằng số được kết hợp bằng cách sử dụng các ký hiệu hoạt động (+, -, × & ÷). Ví dụ, 10x + 63 và 5x – 3 là các ví dụ về biểu thức đại số.

Một biểu thức hữu tỉ được định nghĩa đơn giản là một phân số ở một trong hai hoặc cả tử số và mẫu số là một biểu thức đại số. Ví dụ về phân số hữu tỉ là: 3 / (x – 3), 2 / (x + 5), (4x – 1) / 3, (x ²  + 7x) / 6, (2x + 5) / (x ²  + 3x – 10), (x + 3) / (x + 6), v.v.

Làm thế nào để chia các phân số thông thường?

Biểu thức hữu tỉ được chia bằng cách áp dụng các bước tương tự được sử dụng để chia các phân số thông thường có số hữu tỉ. Số hữu tỉ là số được biểu diễn dưới dạng p / q; trong đó ‘p’ và ‘q’ là các số nguyên và q ≠ 0. Nói cách khác, một số hữu tỉ đơn giản là một phân số trong đó số nguyên a là tử số và số nguyên b là mẫu số.

Ví dụ về số hữu tỉ bao gồm:
2/3, 5/8, -3/14, -11 / -5, 7 / -9, 7 / -15 và -6 / -11, v.v.

Phép chia các phân số thông thường được thực hiện bằng cách nhân phân số thứ nhất với nghịch đảo của phân số thứ hai. Ví dụ, để chia 4/3 ÷ 2/3, bạn chỉ cần tìm tích của phân số thứ nhất và nghịch đảo của phân số thứ hai; 4/3 x 3/2 = 2.

Các ví dụ khác về phép chia số hữu tỉ là:

9/16 ÷ 5/8 = 9/16 × 8/5
= (9 × 8) / (16 × 5) = 72/80
= 9/10
-6/25 ÷ 3/5 = -6/25 × 5 / 3
= {(-6) × 5} / (25 × 3)
= -30/75
= -2/5

Làm thế nào để chia biểu thức hợp lý?

Tương tự, khi chia biểu thức hữu tỉ, chúng ta đảo hoặc lật biểu thức thứ hai và nhân nó với biểu thức thứ nhất.

Dưới đây là tóm tắt các bước được thực hiện khi chia biểu thức hữu tỉ:

• Hoàn toàn trừ mẫu số và tử số của tất cả các biểu thức.
• Thay dấu chia (÷) bằng dấu nhân (x) và tìm số nghịch đảo của phân số thứ hai.
• Giảm phân số nếu có thể.
• Bây giờ viết lại yếu tố còn lại.

ví dụ 1

Chia 4x / 3 ÷ 7y / 2

Giải pháp

4x / 3 ÷ 7y / 2 = 4x / 3 * 2 / 7y

= 8x / 21 năm

Xem thêm:

Mẹo giải biểu thức đại số đơn giản dễ dàng từ A – Z

Đại số cơ bản là gì? Tại sao chúng ta cần học Đại số?

Ví dụ 2

Chia (( x  + 3) / 2x ² ) ÷ (4 / 3x)

Giải pháp

Đổi dấu chia thành dấu nhân và đảo ngược biểu thức thứ hai;

= ( x  + 3 / 2x ² ) × (3x / 4)

Nhân tử số và mẫu số riêng biệt nếu chúng không thể trừ được thừa số;

= [( x  + 3) × 3x] / (2x ²  × 4)

= (3x ²  + 9x) / 8x ²

Vì có một thừa số chung của x ở cả tử số và mẫu số, do đó, biểu thức này có thể được đơn giản hóa là;

(3x ²  + 9x) / 8x ²  =  x (3x + 9) / 8x ²

= (3x + 9) / 8x

Ví dụ 3

Chia nhỏ và sau đó đơn giản hóa.

(x ²  - 4) / (x + 6) ÷ (x + 2) / (2x + 12)

Giải pháp

Nhân biểu thức đầu tiên với nghịch đảo của biểu thức thứ hai;

Nghịch đảo của phân số thứ hai (x + 2) / (2x + 12x) là (2x + 12x) / (x + 2)

(x ²  - 4) / (x + 6) ÷ (x + 2) / (2x + 12) = (x ²  - 4) / (x + 6) * (2x + 12x) / (x + 2)

= Bây giờ nhân tử số và mẫu số.

= [(x ²  - 4) (2x + 12)] / [(x + 6) (x + 2)]

Hãy cộng các số hạng vào tử số và loại bỏ các thừa số chung

= [(x + 2) (x – 2) * 2 (x + 6)] / (x + 6) (x + 2)

Viết lại phân số còn lại;

= 2 (x – 2) / 1 = 2x − 4

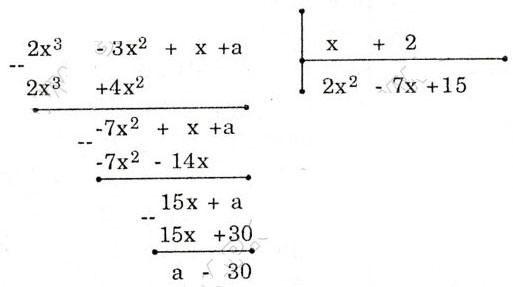
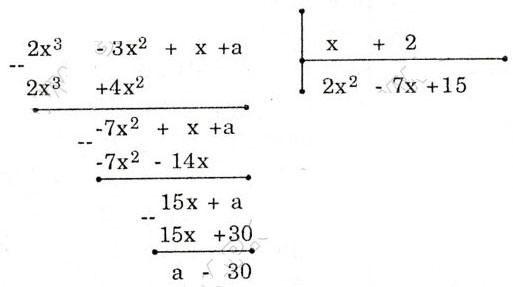
Ví dụ 4

Chia ( x  + 5) / ( x  – 4) ÷ ( x  + 1) / x

Giải pháp

Tìm nghịch đảo của biểu thức thứ hai;

Đối ứng của ( x  + 1) / x = x / x + 1

Bây giờ nhân các phân số;

= (( x  + 5) *  x ) / (( x  – 4) * ( x  + 1))

= ( x ²  + 5x) / ( x ²  – 4x +  x  – 4)

= ( x ²  + 5x) / ( x ²  – 3x – 4)

Ví dụ 5

Đơn giản hóa {(12x – 4x ² ) / (x ² + x – 12)} ÷ {(x ² – 4x) / (x ² + 2x – 8)}

Giải pháp

Đảo phân số thứ hai và nhân;

= {(12x – 4x ² ) / (x ² + x – 12)} * {(x ² + 2x – 8) / (x ² – 4x)}

Tính cả tử số và mẫu số của mỗi biểu thức;

= {- 4x (x – 3) / (x-3) (x + 4)} * {(x – 2) (x + 4) / x (x + 2) (x – 2)}

Rút gọn hoặc hủy bỏ các biểu thức và viết lại các thừa số còn lại;

= -4 / x + 2

Câu hỏi thực hành

Hãy đơn giản hóa các biểu thức hữu tỉ sau:

1. 2x / 4y ÷ 3y / 4xy ²
2. (8x ² – 6x / 4 – x) ÷ (4x ² -x – 3 / x ² -16) ÷ (2x + 8 / -5x -5).
3. (x ² – 7x + 10 / x ² – 9x + 14) ÷ (x ² + 6x + 5 / x ² – 6x -7)
4. (2x + 1 / x ² – 1) ÷ (2x ² + x / x + 1)
5. (-3x ² + 27 / x ³ – 1) ÷ (x – 3x / 7x ³ + 7x ² + 7x) ÷ (21 / x – 1)
6. (x ² – 5x – 14 / x ² – 3x + 2) ÷ (x ² – 14x + 49 / x ² – 4)
7. Khi (4x + 55) chia hết cho (2x + 3) thì được kết quả là 9. Tìm giá trị của x.

Câu trả lời

1. 2x ² /3
2. 5x
3. x + 2 / x-2
4. 1 / x (x – 1)
5. – x – 3
6. (x + 2) ² / (x – 1) (x – 7)
7. 2