Làm thế nào để đơn giản hóa biểu thức nhanh nhất?

Đơn giản hóa biểu thức – Giải thích & Ví dụ

Học cách đơn giản hóa biểu thức là bước quan trọng nhất để hiểu và thành thạo đại số. Đơn giản hóa các biểu thức là một kỹ năng toán học rất hữu ích vì nó cho phép chúng ta thay đổi biểu thức phức tạp hoặc khó hiểu thành dạng đơn giản và nhỏ gọn hơn. Nhưng trước đó chúng ta phải biết biểu thức đại số là gì.

Biểu thức đại số là một cụm từ toán học trong đó các biến và hằng số được kết hợp bằng cách sử dụng các ký hiệu hoạt động (+, -, × & ÷). Ví dụ, 10x + 63 và 5x – 3 là các ví dụ về biểu thức đại số.

Trong bài này, chúng ta sẽ học một vài thủ thuật về cách đơn giản hóa bất kỳ biểu thức đại số nào.

Làm thế nào để đơn giản hóa biểu thức?

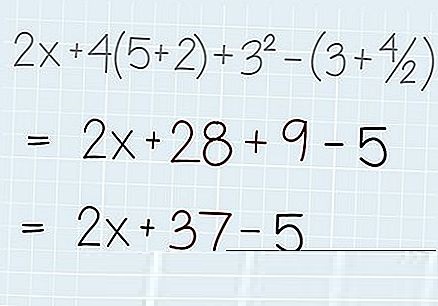
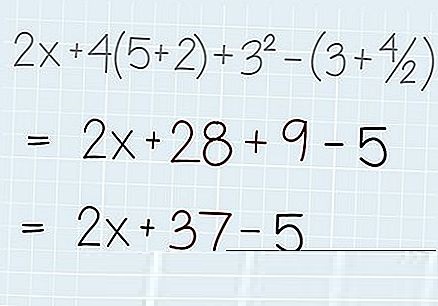
Đơn giản hóa một biểu thức đại số có thể được định nghĩa là quá trình viết một biểu thức ở dạng nhỏ gọn và hiệu quả nhất mà không ảnh hưởng đến giá trị của biểu thức ban đầu.

Quá trình này đòi hỏi phải thu thập các thuật ngữ giống như, ngụ ý, thêm hoặc bớt các thuật ngữ trong một biểu thức.

Hãy tự nhắc mình một số thuật ngữ quan trọng được sử dụng khi đơn giản hóa một biểu thức:

• Biến là một ký tự có giá trị chưa biết trong biểu thức đại số.
• Hệ số là một giá trị số được sử dụng cùng với một biến.
• Hằng số là một thuật ngữ có giá trị xác định.
• Giống như các điều khoản là các biến có cùng chữ cái và quyền lực. Giống như các điều khoản đôi khi có thể chứa các hệ số khác nhau. Ví dụ, 6x ²và 5x ²  giống như các số hạng vì cả hai đều có biến với số mũ giống nhau. Tương tự, 7yx và 5xz không giống như các số hạng vì mỗi số hạng có các biến khác nhau.

Để đơn giản hóa bất kỳ biểu thức đại số nào, sau đây là các quy tắc và bước cơ bản:

• Loại bỏ bất kỳ biểu tượng nhóm nào như dấu ngoặc và dấu ngoặc đơn bằng cách nhân các thừa số.
• Sử dụng quy tắc số mũ để loại bỏ nhóm nếu các điều khoản có chứa số mũ.
• Kết hợp các thuật ngữ tương tự bằng phép cộng hoặc phép trừ
• Kết hợp các hằng số

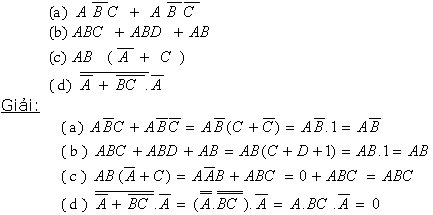
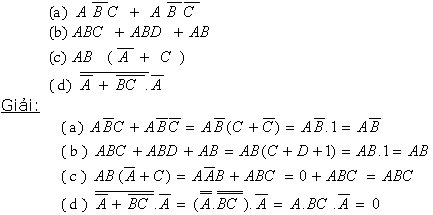
ví dụ 1

Đơn giản hóa 3 x ²  + 5 x ²

Giải pháp

Vì cả hai số hạng trong biểu thức đều có cùng số mũ nên chúng tôi kết hợp chúng lại;

3 x ²  + 5 x ²  = (3 + 5) x ²  = 8 x ²

Ví dụ 2

Đơn giản hóa biểu thức: 2 + 2x [2 (3x + 2) +2)]

Giải pháp

Đầu tiên, hãy tính toán bất kỳ thuật ngữ nào trong ngoặc bằng cách nhân chúng với nhau;

= 2 + 2x [6x + 4 +2] = 2 + 2x [6x + 6]

Bây giờ loại bỏ các dấu ngoặc bằng cách nhân bất kỳ số nào bên ngoài nó;

2 + 2x [6x + 6] = 2 + 12x ² + 12x

Biểu thức này có thể được đơn giản hóa bằng cách chia mỗi số hạng cho 2 như;

12x ^2/2 + 12x / 2 + 2/2 = 6 x ² + 6x + 1

Xem thêm:

Hướng dẫn giải biểu thức phân chia dễ hiểu nhất hiện nay

Đại số cơ bản là gì? Tại sao chúng ta cần học Đại số?

Ví dụ 3

Đơn giản hóa 3 x  + 2 ( x  – 4)

Giải pháp

Trong trường hợp này, không thể kết hợp các từ khi chúng vẫn còn trong ngoặc đơn hoặc bất kỳ dấu hiệu nhóm nào. Do đó, hãy loại bỏ dấu ngoặc đơn bằng cách nhân bất kỳ hệ số nào bên ngoài nhóm với tất cả các số hạng bên trong nó.

Do đó, 3 x  + 2 ( x  – 4) = 3 x  + 2 x  – 8

= 5 x  – 8

Khi một dấu trừ đứng trước một nhóm, nó thường ảnh hưởng đến tất cả các toán tử bên trong dấu ngoặc đơn. Điều này có nghĩa là một dấu trừ đứng trước một nhóm sẽ thay đổi phép toán cộng thành phép trừ và ngược lại.

Ví dụ 4

Đơn giản hóa 3 x  – (2 –  x )

Giải pháp

3 x  – (2 –  x ) = 3 x  + (–1) [2 + (- x )]

= 3 x  + (–1) (2) + (–1) (- x )

= 3 x  – 2 +  x

= 4 x  – 2

Tuy nhiên, nếu chỉ có một dấu cộng đứng trước nhóm, thì dấu ngoặc đơn sẽ bị xóa.

Ví dụ , để đơn giản hóa 3 x  + (2 –  x ), dấu ngoặc nhọn được loại bỏ như hình dưới đây:

3x + (2 – x) = 3x + 2 – x

Ví dụ 5

Đơn giản hóa 5 (3x-1) + x ((2x) / (2)) + 8 – 3x

Giải pháp

15x – 5 + x (x) + 8 – 3x

15x – 5 + x ²  + 8 – 3x.

Bây giờ kết hợp các điều khoản tương tự bằng cách thêm và trừ các điều khoản;

x ²  + (15x – 3x) + (8 – 5)

x ²  + 12x + 3

Ví dụ 6

Đơn giản hóa x (4 – x) – x (3 – x)

Giải pháp

x (4 – x) – x (3 – x)

4x – x ²  – x (3 – x)

4x – x ²  – (3x – x ² )

4x – x ²  – 3x + x ²  = x

Câu hỏi thực hành

Đơn giản hóa từng biểu thức sau:

1. 2 giây + 3t – s + 5t + 4 giây
2. 2a – 4b + 3ab -5a + 2b
3. x (2x + 3y -4) – x  ²  + 4xy – 12
4. 4 (2x + 1) – 3x
5. 4 (p – 5) +3 (p +1)
6. [2x  ³ y ² ] ³
7. 6 (p + 3q) – (7 + 4q)
8. 4 giây -2 giây – 3 (rs +1) – 2 giây
9. [(3 – x) (x + 2) + (-x + 4) (7x + 2) – (x – y) (2x – y)] – 3x ²  – 7x + 5